About
Topics
Measurement of length and timeDescription
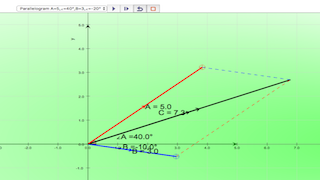
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical,What is shown here?
1. What are the x and y components of the RED vector A?2. record down on a piece of paper.
3. What are the x and y components of the BLUE vector B?.
4. record down on a piece of paper.
5. now, you have the values of (Ax, Ay) = _______ and (Bx, By) = _______
How to calculate the resultant of 2 vectors?
1. click PLAY to visualise the meaning of addition of vector A with B.2. What are the components of this vector sum?
3. How do they relate to the components of the original (RED and BLUE) vectors?
4. The vector (BLACK) sum C = (Cx, Cy) is now a vector that reaches from the tail of the first (RED) A = (Ax,Ay) vector to the head of the second (BLUE) B = (Bx,By) vector.
5. test yourself whether you have enough practice calculating C = (Cx,Cy).
Other interesting fun activities
1. this model can be used to calculate any A & B vectors.4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/vector-addition-model.html
Sample Learning Goals
(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of eachVersion:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Learning Objectives: https://sites.google.com/moe.edu.sg/a-level-physics-tlg/foundations-of-physics/quantities-measurement
Learning Outcomes: H2 - 1(h)(i)(j)
Curriculum Emphasis: Ways of Thinking and Doing [WOTD https://vle.learning.moe.edu.sg/mrv/moe-library/lesson/view/c788167e-5865-4166-b147-89330b50b6b2/cover SLS lesson includes questions that can be repeated indefinitely with random values inserted.
Vector Addition Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences.
- What is a vector? Provide two examples of vector quantities.
- Describe the process of resolving a vector into its components.
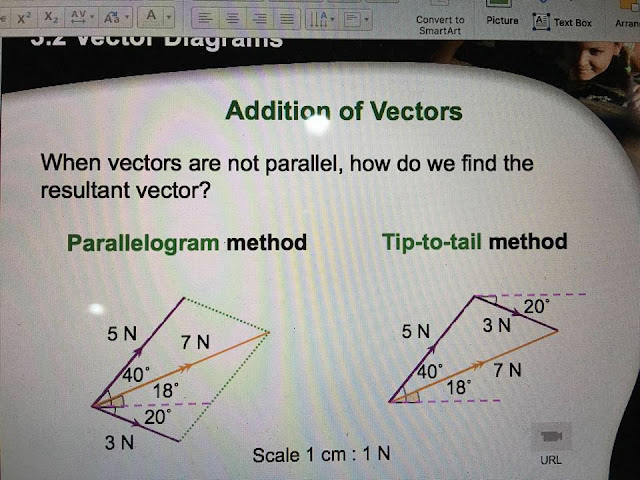
- What is the parallelogram method of vector addition? How is the resultant vector represented in this method?
- Explain the tip-to-tail method of vector addition. How does this method differ from the parallelogram method?
- How do you determine the x and y components of a vector given its magnitude and direction?
- If you know the x and y components of two vectors, how do you calculate the x and y components of their resultant vector?
- What is the significance of the magnitude and direction of the resultant vector in vector addition?
- Why might resolving vectors into components be useful in real-world physics problems?
- Describe a situation where understanding vector addition is crucial.
- How can the interactive simulation model on the Open Source Physics @ Singapore website help you understand vector addition?
Quiz Answer Key
- A vector is a quantity that has both magnitude (size) and direction. Examples include displacement, velocity, and force.
- Resolving a vector involves breaking it down into two perpendicular components, typically along the x and y axes. This is done using trigonometry, where the x-component is the magnitude times the cosine of the angle, and the y-component is the magnitude times the sine of the angle.
- The parallelogram method involves drawing two vectors with their tails at the same point. Then, complete the parallelogram using these vectors as sides. The diagonal drawn from the shared tail point represents the resultant vector.
- In the tip-to-tail method, the tail of the second vector is placed at the head of the first vector. The resultant vector is drawn from the tail of the first vector to the head of the second. It differs from the parallelogram method in its visual representation, but yields the same resultant vector.
- You can determine the x and y components using trigonometry: x-component = magnitude * cos(angle), and y-component = magnitude * sin(angle). The angle is measured with respect to the horizontal axis.
- The x-component of the resultant is the sum of the x-components of the individual vectors. Similarly, the y-component of the resultant is the sum of the y-components of the individual vectors.
- The magnitude of the resultant vector represents the total magnitude of the combined vectors, while the direction indicates the overall direction of the combined effect.
- Resolving vectors is useful in situations where forces or motions are not aligned with simple coordinate systems. It allows you to analyze the impact of each vector along specific directions.
- Understanding vector addition is crucial in navigation, where you need to consider the direction and speed of the wind and water currents to calculate the course and speed of a boat or plane.
- The interactive simulation allows you to manipulate vectors and visually observe the results of adding them using both parallelogram and tip-to-tail methods. This helps to build intuition and understanding of vector addition concepts.
Essay Questions
- Compare and contrast the parallelogram and tip-to-tail methods of vector addition. Discuss the advantages and disadvantages of each method.
- Explain the significance of resolving vectors into components. Provide a real-world example from physics where resolving vectors is essential for problem-solving.
- Discuss the role of vector addition in understanding projectile motion. How are the horizontal and vertical components of velocity treated independently?
- Explain how vector addition applies to forces acting on an object. Describe the conditions required for an object to be in equilibrium under the influence of multiple forces.
- Explore the applications of vector addition in fields beyond physics, such as computer graphics, engineering, or navigation. Choose one specific application and discuss how vector addition principles are utilized.
Glossary of Key Terms
- Vector: A quantity that has both magnitude (size) and direction.
- Scalar: A quantity that only has magnitude, but no direction.
- Magnitude: The size or length of a vector, representing its numerical value.
- Direction: The orientation of a vector in space, typically indicated by an angle.
- Components: The projections of a vector along the x and y axes (or any other chosen set of perpendicular axes).
- Resultant Vector: The vector obtained by adding two or more vectors together, representing the combined effect of the individual vectors.
- Parallelogram Method: A graphical method of vector addition where the resultant vector is the diagonal of the parallelogram formed by the two added vectors.
- Tip-to-Tail Method: A graphical method of vector addition where the tail of the second vector is placed at the head of the first vector, and the resultant is drawn from the tail of the first to the head of the second.
- Resolution of Vectors: The process of breaking down a vector into its components along specific directions.
- Equilibrium: A state where an object is at rest or moving with constant velocity because all forces acting on it are balanced.
Briefing Document: Vector Addition and Components
Source: Excerpts from "Parallelogram and Tip to Tail Method Vector Addition A + B = C JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore"
Main Themes:
- Understanding Vectors: The document introduces the concept of vectors as quantities possessing both magnitude and direction. It emphasizes that displacement, velocity, acceleration, and force are examples of vector quantities.
- Vector Addition: The document focuses on two key methods for vector addition:
- Parallelogram Method: This visual method uses a parallelogram constructed from the two vectors being added. The resultant vector is represented by the diagonal of the parallelogram.
- Tip-to-Tail Method: This method involves placing the tail of the second vector at the tip of the first vector. The resultant vector is drawn from the tail of the first vector to the tip of the second vector.
- Vector Components: The document highlights the importance of resolving vectors into their horizontal (x) and vertical (y) components. This process simplifies vector addition, particularly when vectors are not aligned with the coordinate axes.
Most Important Ideas/Facts:
- Vectors in Real Life: The document connects the abstract concept of vectors to real-world applications by providing examples of vector quantities like displacement, velocity, acceleration, and force.
- Resolving Vectors: The document explains that resolving a vector means breaking it down into its horizontal and vertical components. This enables calculations using simple trigonometry.
- Calculating Resultant Vector: The document provides a step-by-step guide for calculating the resultant vector (C) from the addition of two vectors (A and B) using their components:
- "The vector (BLACK) sum C = (Cx, Cy) is now a vector that reaches from the tail of the first (RED) A = (Ax,Ay) vector to the head of the second (BLUE) B = (Bx,By) vector."
- Beyond Horizontal and Vertical: The document points out that resolving vectors is not limited to horizontal and vertical axes. It can be adapted to resolve vectors along and perpendicular to any desired direction, such as a slope.
- Interactive Learning: The document promotes interactive learning by referencing a JavaScript HTML5 applet simulation model designed to help students visualize and practice vector addition and component calculations.
Key Quotes:
- "A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities."
- "In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes."
Overall Significance: The document serves as a concise introduction to the fundamental principles of vectors, vector addition, and vector components. It emphasizes both conceptual understanding and practical application, utilizing visual aids and interactive tools to enhance learning.
Learning Design
London Knowledge Lab - Institute of Education
How to Use
Topics
Measurement of length and time
Description
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical,
What is shown here?
1. What are the x and y components of the RED vector A?
2. record down on a piece of paper.
3. What are the x and y components of the BLUE vector B?.
4. record down on a piece of paper.
5. now, you have the values of (Ax, Ay) = _______ and (Bx, By) = _______
How to calculate the resultant of 2 vectors?
1. click PLAY to visualise the meaning of addition of vector A with B.
2. What are the components of this vector sum?
3. How do they relate to the components of the original (RED and BLUE) vectors?
4. The vector (BLACK) sum C = (Cx, Cy) is now a vector that reaches from the tail of the first (RED) A = (Ax,Ay) vector to the head of the second (BLUE) B = (Bx,By) vector.
5. test yourself whether you have enough practice calculating C = (Cx,Cy).
Other interesting fun activities
1. this model can be used to calculate any A & B vectors.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/vector-addition-model.html
Sample Learning Goals
(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each
Version:
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/20-vector-addition-a-b-c-model |
Practice
http://goo.gl/forms/2ITP4YvbZp
wanna see what others have done? click here
Research
[text]
Video
https://notebooklm.google.com/notebook/524060f5-effd-4605-b401-2bad3524c6d0/audio
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
- http://ophysics.com/k11.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
Vector Addition FAQ
What is a vector?
A vector is a quantity that possesses both magnitude (size) and direction. Examples of vector quantities include displacement, velocity, acceleration, and force.
How are vectors represented graphically?
Vectors are typically represented graphically as arrows. The length of the arrow represents the magnitude of the vector, while the direction the arrow points represents the direction of the vector.
What are the components of a vector?
Vectors can be broken down into components along the x (horizontal) and y (vertical) axes. These components represent the contribution of the vector in each direction.
How do you add vectors using the parallelogram method?
To add vectors using the parallelogram method:
- Draw the two vectors to be added with their tails originating from the same point.
- Complete the parallelogram using the two vectors as sides.
- The diagonal of the parallelogram, originating from the common tail, represents the vector sum (resultant vector).
How do you add vectors using the tip-to-tail method?
To add vectors using the tip-to-tail method:
- Draw the first vector.
- Draw the second vector with its tail at the head of the first vector.
- The vector drawn from the tail of the first vector to the head of the second vector represents the vector sum.
How do you calculate the components of the resultant vector?
The components of the resultant vector (C) are the sum of the corresponding components of the original vectors (A and B):
- Cx = Ax + Bx
- Cy = Ay + By
What are scalar quantities?
Scalar quantities are quantities that have only magnitude, but no direction. Examples of scalar quantities include mass, temperature, and time.
How do vectors differ from scalar quantities?
Vectors differ from scalar quantities because they have both magnitude and direction. While a scalar quantity can be fully described by a single number, a vector requires both a magnitude and a direction for its complete description.
- Details
- Parent Category: 01 Foundations of Physics
- Category: 01 Measurements
- Hits: 18185