About
Spontaneous perception of cardinal numbers
(Members in a set )
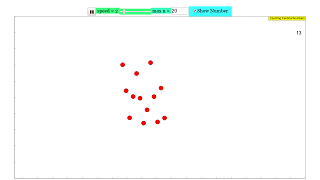
When the simulation is opened a field is shown with some red dots in random distribution. They are sufficiently close to perceive their number at a glance.
The number of points displayed is changed periodically at random between 1 and a maximum number that can be edited in the number field. Default value is a maximum of 5 dots.
A slider defines the changes per second between 1 and 10.
A narrow second window shows how many points are displayed at any moment. This window can be concealed by a check box. It can also be drawn out of the field of view of the experimenting person to allow control by a second person.
Try to perceive with certainty the number of points without counting (scanning).
Up to 5 points this should be no problem. Beyond 7 it will be barely possible. This finding does not vary substantially with moderate changes in the speed of presentation.
Spontaneus perception and skill of calculation
Cardinal numbers indicate the number of elements in a set, i.e. the number of elements in a group with some common identifiable quality (not necessarily identity!) Even very young children will identify 2 apples, which of course are not identical in their appearance in a mathematical sense, as 2 apples.
Ordinal numbers characterize the consecution of elements in a set. Young children will count a number of apples in a row as 1, 2, 3 and identify a certain element as 3, meaning it is the third one.
To the skilled adult this differentiation blurs when calculating. When asked 3 + 5 he will immediately answer 8, as if having added the cardinal numbers 3 and 5.
A young child solves the same problem openly using ordinal numbers, starting with counting the first row 1st, 2nd, 3rd, and continuing in the second row 4th, 5th, 6th, 7th, 8th. Alas! The result is 8.
For children of about 3 years it is a difficult task to calculate with ordinal numbers even for very small numbers. Yet they love to do it as a game. It takes a lot of repetition and exercise to climb from 1 + 1 (which is grasped very quickly) to 4 + 1 , and it is very charming how they use their fingers, open or concealed, to "cheat" by counting.
Quite surprisingly one never gets much beyond 5 in the spontaneous perception of cardinal numbers. Any skill to do fast addition beyond that small number range is the result of memorizing the outcome of numerous combinations and of rules, and hence of hard work. Insofar persistent exercise in basic calculation and the learning of multiplication tables is no boring ill treatment of kids, but the basis of an indispensible cultural skill.
Most adults do not realize that their skill in the perception of cardinal numbers does not go beyond that of young children (and that of well trainable animals, by the way), and that it cannot really be trained. Their skill (if they have it!) is based on a history of memorization of results and rules.
E1: Conceal the number window and let the animation run at 1 step per second, and for a maximum of 5 points.
Do you always recognize the number of points without counting or scanning?
E2: Increase the speed − which makes counting more difficult. Do you experience a great difference?
E3: Increase the maximum number and test where your limit of secure perception is at different speeds.
E4: Test if you perceive this limit consistently or just when the points form a regular pattern.
E5: Let another person control you.
E6: Draw a diagram of the number of true hits as a function of the maximum number of points, and another one of the dependence on speed.
E7: Let your friends bet on their maximum, and show them their limit.
E8: Try to draw conclusions on what your findings mean when applied to the teaching of young children.
This file was created by Dieter Roess in December 2009
This simulation is part of
“Learning and Teaching Mathematics using Simulations
– Plus 2000 Examples from Physics”
ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee
Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee
Sample Learning Goals
[text]
For Teachers
Research
[text]
Video
[text]
Version:
- http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
- http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Wei Chiong
- Parent Category: Mathematics
- Category: Numbers and Algebra
- Hits: 3812