About

 

Translations

Code	Language		Translator	Run

Credits

Fernando Fernandes; lookang

Briefing Document: Acid-Base Titration Simulation Model

1. Overview:

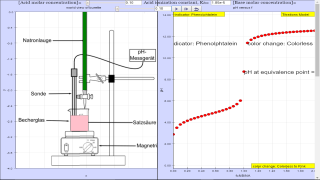
This document analyzes a JavaScript simulation model designed to teach acid-base titrations. The model, created by Fernando Silva Fernandes, focuses on titrations involving monoprotic acids and monofunctional strong bases. It is an educational tool meant to complement experimental work by visually and computationally demonstrating the concepts involved. The simulation allows for manipulation of various parameters and displays the titration curve, equivalence point, and suitable indicator for a given titration.

2. Core Concepts & Functionality:

• Titration Process: The model simulates the process of titrating a known volume of an acid with a standardized base, following the standard laboratory practice. It emphasizes the determination of the unknown acid concentration by adding base until the equivalence point is reached.
• "Take a flask with a known volume (VA) of an aqueous solution of a monoprotic acid whose concentration is unknown. In a buret there is a padronized (well-known molar concentration) aqueous solution of a monofunctional strong base (sodium hydroxide, for example). Add to the flask a few drops of a suitable visual indicator and start pouring, slowly, the base over the acid."
• Equivalence Point: The model highlights the importance of the equivalence point, where the acid is completely neutralized by the base. It calculates the pH at the equivalence point.
• "The titration end point (equivalence point) is detected by a sudden change of the indicator color."
• "Therefore, the titration coordinate (f=NB/NA) is equal to 1 at the equivalence point."
• Visual Indicators: The simulation addresses the use of visual indicators to detect the equivalence point. It also selects a proper indicator based on the calculated equivalence point pH.
• "The indicator is chosen accordingly to its effectiveness color range, that is, the equivalence point pH should be approximately at the middle of that range."
• Titration Curve: The simulation generates a titration curve with 41 steps, plotting pH values against the titration coordinate (f). This shows how the pH changes throughout the titration.
• "As the titration has 41 steps, we should work out a titration curve with 41 pH values, stored in the array pH(i), in function of f(i)."
• Mathematical Modeling: The model employs mathematical equations to calculate pH during different stages of the titration. It uses two main equations: one before the equivalence point (BEP) and another at and after the equivalence point (EPAEP).
• "Before the equivalence point (0⋜ f(i) <1) the titration process obeys the equation: [H3O+]3 + (Ka+BT) * [H3O+]2 + (KABT - KaAT - Kw)[H3O+] - KaKw = 0 (BEP)"
• "The titration process for f(i) ⋝ 1 obeys the equation: [H3O+]3 + (BE+ST+Ka) * [H3O+]2 - (KW-BE Ka)[H3O+] - KaKw = 0 (EPAEP)"*
• Ionization Constants: The model incorporates the acid ionization constant (Ka) to characterize the acid, and takes into account the water ionic product (Kw). It highlights that since the base is assumed to be strong (fully ionized) its constant is not considered.
• "The acid is characterized by the ionization constant (Ka); the default value is for acetic acid. As the base is assumed strong (fully ionized) its constant (Kb) is not a program input."
• Numerical Solution: The model uses the method of successive bisections to numerically solve the equations, finding the hydrogen ion concentration and thus calculating pH.
• "The equations are numerically solved by the method of successive bisections."

3. Key Parameters and Variables:

• VA: Volume of the acid solution (in cm³)
• CA: Molar concentration of the acid
• CB: Molar concentration of the base
• Ka: Acid ionization constant
• f: Titration coordinate (NB/NA)
• NA: Number of moles of acid
• NB: Number of moles of base
• VB: Volume of base used
• AT: Total acid concentration in the mixture
• BT: Total base concentration in the mixture
• ST: Concentration of salt
• BE: Concentration of base in excess
• pH(i): Array of pH values at each titration step.
• [H3O+]: Hydronium ion concentration.
• Kw: Water ionic product

4. Educational Value & Applications:

• Visualization: The simulation provides a visual representation of an abstract concept, allowing students to see the relationship between volume added and the pH change.
• Parameter Manipulation: Students can manipulate parameters such as the acid ionization constant (Ka), concentrations, and volumes to explore how they influence the titration process and the choice of a proper indicator.
• "To this end, different simulations should be done by changing the [Acid] and [Base] fields for a given acid."
• Conceptual Understanding: The simulation helps students grasp fundamental concepts like the equivalence point, the role of indicators, and the importance of the acid ionization constant.
• Exploration and Inquiry: The included questions ("Incidentally, has the value of VA any influence on the titration results? Why?", etc.) encourage students to engage in critical thinking and inquiry.
• Trial and Error: The program facilitates trial and error, allowing students to investigate the suitability of indicators for different acid concentrations.
• "Of course, the indicator choice requires a previous trial and error study to screen possible concentration bands of the acidic sample and assess whether or not the same indicator is appropriate for each band."

5. Technical Details:

• Platform: The simulation is written in JavaScript and designed to run in browsers on various devices.
• Underlying Tool: It was created using Easy Java Simulations (EJS), a modeling tool that allows for the creation of standalone JavaScript programs.
• "The Titrations JS Model was developed by Fernando M.S. Silva Fernandes (Centre for Structural Chemistry, Faculty of Sciences, University of Lisboa) using version 5.1 of the Easy Java Simulations (EJS) modeling tool..."
• Source Code: The model provides a clear explanation of the derivation of the mathematical equations used, as well as the method of numerical solution using successive bisections.

6. Limitations and Potential Expansions:

• Monoprotic Acids and Monofunctional Strong Bases: The model is limited to these types of substances.
• "This application is restricted to monoprotic acids and monofunctional strong bases."
• Suggestions for further improvement: The document suggest extending the code to include weak bases and polyfunctional acids and bases.
• "Finally, a suggestion: the code can be generalized to comprise weak bases and polifunctional acids and bases."

7. Conclusion:

This JavaScript simulation model provides an effective and engaging way for students to learn about acid-base titrations. By combining visual elements with mathematical modeling, it facilitates conceptual understanding and allows for active exploration and experimentation. Its limitations, such as the restriction to monoprotic acids, provide opportunities for future expansions, making it a useful tool in a chemistry education context.

 

Acid-Base Titration Study Guide

Quiz

1. What is the purpose of a titration experiment? Titration is a process used to determine the unknown concentration of a substance (analyte) by reacting it with a solution of known concentration (titrant). In this case, it is used to find the concentration of the monoprotic acid in the flask.
2. What is a monoprotic acid? A monoprotic acid is an acid that donates only one proton (H+) per molecule during an acid-base reaction. Examples would be hydrochloric acid or acetic acid.
3. What is a standardized base? A standardized base is a base solution with a precisely known concentration, determined through a prior titration against a primary standard.
4. How is the equivalence point of a titration visually detected? The equivalence point is visually detected by the use of a suitable indicator that undergoes a distinct color change when the pH of the solution reaches the appropriate range, which corresponds to the equivalence point of the titration.
5. What does the titration coordinate (f) represent? The titration coordinate, f, represents the ratio of moles of the added base (NB) to the moles of acid initially present (NA), with f=1 indicating the equivalence point.
6. What factors influence the pH at the equivalence point in a weak acid strong base titration? The pH at the equivalence point is influenced by the acid ionization constant (Ka), the initial concentration of the acid ([Acid]), and the concentration of the base ([Base]).
7. What are the two key chemical equilibria to consider before the equivalence point? Before the equivalence point, the two key chemical equilibria to consider are the acid ionization equilibrium (HA + H2O ⇌ A- + H3O+) and the water auto-ionization equilibrium (H2O + H2O ⇌ H3O+ + OH-).
8. What chemical species need to be considered at and after the equivalence point? At and after the equivalence point, the chemical species to consider are the salt (NaA) that is formed, the hydroxide ions and hydronium ions from water autoionization, and any excess base that has been added.
9. Why is the hydrolysis of the salt important to consider in a weak acid-strong base titration? In a weak acid strong base titration, the salt formed can undergo hydrolysis which will change the concentration of hydroxide and hydronium ions in the solution. Because of hydrolysis, the equivalence point pH will not always be 7.
10. What is the bisection method and how is it used in the simulation? The bisection method is a numerical method for finding the roots of an equation. The simulation uses this method to solve for hydrogen ion concentration by repeatedly dividing an interval where the root is known to be present and narrowing in on the exact value of [H3O+].

Essay Questions

1. Explain the significance of the equivalence point in an acid-base titration, discussing its relationship to the stoichiometry of the reaction and the choice of indicator. How do the chemical equilibria considered before and after the equivalence point influence the shape of a titration curve?
2. Describe the differences in titration curves that would be observed between a strong acid-strong base titration and a weak acid-strong base titration. Explain the chemical reactions and equilibria that lead to these differences.
3. The simulation allows for manipulation of the ionization constant (Ka). How does the strength of an acid, as indicated by its Ka value, affect the titration curve and the choice of indicator? Discuss examples using acids of varying strength.
4. Explain the importance of considering the electroneutrality condition in the derivation of the model equations for acid-base titrations. How does this principle relate to the charge balance within the solution at different stages of the titration?
5. Analyze the computational methods used in the simulation for determining the pH during a titration. How does the bisection method function, and why is it suitable for the equations that describe the changes in hydronium ion concentration during titration?

Glossary

• Titration: A technique used to determine the concentration of a solution (analyte) by reacting it with a solution of known concentration (titrant).
• Monoprotic Acid: An acid that donates only one proton (H+) per molecule during an acid-base reaction.
• Standardized Base: A base solution with a precisely known concentration.
• Equivalence Point: The point in a titration where the moles of titrant added are stoichiometrically equivalent to the moles of analyte present in the solution.
• Indicator: A substance that changes color depending on the pH of the solution, used to visually detect the equivalence point of a titration.
• Titration Coordinate (f): The ratio of moles of base added to moles of acid initially present (f=NB/NA).
• Acid Ionization Constant (Ka): A measure of the strength of an acid, representing the equilibrium constant for the dissociation of the acid into ions.
• Hydrolysis: The reaction of a salt with water, producing hydronium or hydroxide ions, which affects pH.
• Electroneutrality: The principle that, in a solution, the total positive charge must equal the total negative charge.
• Bisection Method: A numerical method for finding the root of a continuous function by repeatedly dividing an interval in half.
• Hydronium Ion (H3O+): The form that a proton takes when dissolved in water and what is used to determine pH.
• Ionic Product of Water (Kw): The product of the concentrations of hydronium and hydroxide ions in water, a constant value at a specific temperature.

Sample Learning Goals

[text]

For Teachers

The Titrations JavaScript Model is a JavaScript program that demonstrates the importance of computer simulation as a complement of experimental work. A typical students training in a chemistry laboratory is the titration of an acidic solution by a padronized base in order to determine the acid concentration in the sample. If the titration is followed by a visual method, a suitable indicator has to be previously chosen to detect the end point of the titration (the so-called equivalence point) by the sudden change of the indicator color. This is a common practice (alternative to using a pH meter) and does not imply the errors that may be thought on the subjective aspect of a color change, providing that the right indicator is chosen. This application is restricted to monoprotic acids and monofunctional strong bases.

Take a flask with a known volume (VA) of an aqueous solution of a monoprotic acid whose concentration is unknown. In a buret there is a padronized (well-known molar concentration) aqueous solution of a monofunctional strong base (sodium hydroxide, for example). Add to the flask a few drops of a suitable visual indicator and start pouring, slowly, the base over the acid.

The titration end point (equivalence point) is detected by a sudden change of the indicator color. Then, the buret scale indicates the volume of the base (VB) used in the neutralization reaction, and as its molar concentration, [Base], is well-known the corresponding number of moles is NB=VB*[Base]/1000. This number is equal to the number of acid moles, NA=NB, that have reacted and as the sample volume is VA, the acid molar concentration is worked out: [Acid] = NA*1000/VA. Therefore, the titration coordinate (f=NB/NA) is equal to 1 at the equivalence point.

The indicator is chosen accordingly to its effectiveness color range, that is, the equivalence point pH should be approximately at the middle of that range.

The simulations determine the pH at the equivalence point and choose the proper indicator from a table included in the program. The acid is characterized by the ionization constant (Ka); the default value is for acetic acid. As the base is assumed strong (fully ionized) its constant (Kb) is not a program input. The pH at equivalence point depends on Ka, [Base] and also on [Acid]. But the acid concentration is precisely what we want to know! Of course, the indicator choice requires a previous trial and error study to screen possible concentration bands of the acidic sample and assess whether or not the same indicator is appropriate for each band. To this end, different simulations should be done by changing the [Acid] and [Base] fields for a given acid. The program can probe wide ranges of Ka, from 10- 10 (very weak acids like hydrocyanic acid and phenol) to 109 (very strong acids like hydrochloric and sulphuric acids), and of [Acid] and [Base].

Credits

The Titrations JS Model was developed by Fernando M.S. Silva Fernandes (Centre for Structural Chemistry, Faculty of Sciences, University of Lisboa) using version 5.1 of the Easy Java Simulations (EJS) modeling tool which can create stand alone JavaScript programs that run in almost any PC browser, tablets and smartphones. Information about EJS is available at: http://www.um.es/fem/Ejs/, and in the OSP ComPADRE collection: http://www.compadre.org/osp/.

Model

Let's take the volume VA (in cm³) of an aqueous solution of a monoprotic acid HA (acetic acid, for example) of molar concentration CA. Then, the number of moles (NA) of the acid in VA is: NA=VA*CA/1000.

Let's drop over the acid a certain number of moles (NB), of a strong monofunctional base (sodium hydroxide, for example), following the procedure by the titration coordinate, f(i)=NB/NA.

Let's change f(i) from 0 to 2 with increments of 0.05, resulting in a titration with 41 steps ( i =0, 1, 2,..., 40). Therefore, step 20 corresponds to the equivalence point.

From NB and the molar concentration of the base (CB), the total volume of the base (VB) at the end of each step is: VB=1000*NB/CB, so the total volume of the mixture (VT) is: VT=VA+VB. It follows that the total concentrations of acid and base in the mixture at the end of each titration step, supposing that have not yet reacted, are, respectively: AT=1000*NA/VT and BT=1000*NB/VT.

As the titration has 41 steps, we should work out a titration curve with 41 pH values, stored in the array pH(i), in function of f(i).

Before the equivalence point (0⋜ f(i) <1) the titration process obeys the equation:

[H₃O⁺]³ + (Ka+BT) * [H₃O⁺]² + (KA*BT - Ka*AT - Kw)*[H₃O⁺] - Ka*Kw = 0 (BEP)

where [H₃O⁺] is the hydronium ion concentration, Ka the acid ionization constant and Kw the water ionic product. AT and BT were defined above. Of course, the only unknown is [H₃O⁺].

Resolving this equation with the different values of AT and BT, the values of pH=- log [H₃O⁺] are determined for the titration process before the equivalence point.

At equivalence point and afterwards (f(i) ⋝ 1):

a) when f(i)=1, NA moles of salt are formed; this is the equivalence point.

b) when f(i)>1, the NA moles of salt, and the NB-NA moles of base in excess have to be taken into account.

The concentrations of salt, and of the base in excess, are respectively: ST=1000*NA/VT and BE=1000*(NB-NA)/VT. The salt and the strong base are totally ionized. The salt, however, undergoes hydrolysis, except in the titrations of strong acids by strong bases; this is why the pH, at the equivalence point, is generally different from 7. The titration process for f(i) ⋝ 1 obeys the equation:

[H₃O⁺]³ + (BE+ST+Ka) * [H₃O⁺]² - (KW-BE *Ka)*[H₃O⁺] - Ka*Kw = 0 (EPAEP)

Resolving this equation with the values of ST and BE, the pH's are determined for the titration process at, and after the equivalence point.     

A few computational detais

The equations are numerically solved by the method of successive bisections.

Once the pH at the equivalence point is determined, the appropriate indicator is chosen from a table included in the code. Both are displayed at the bottom of the plotting panel. The respective color change of the indicator is also displayed at the panel top.

The default variable values are for acetic acid (Ka=1.85E-5), with CA=0.10M, VA=50 cm³ and CB=0.10M.

The respective fields, however, can be edited. Try, for example, Ka=1E9 for a strong acid or/and change the values of the other variables. To this end, please Reset the simulation and actualize each new value by pressing the Return/Enter key.

The program has been tested in a wide range of Ka's: from 10^{- 10} (for very weak acids like hydrocyanic acid and phenol) to 10⁹ (for very strong acids like hydrochloric and sulphuric acids). Nonetheless, if any inconsistency is found, please let us know.

- Incidentally, has the value of VA any influence on the titration results? Why?

- As the model is intended for strong bases, sodium hydroxide (NaOH) was chosen. Changing the name to another strong base, KOH for example, would it alter the results? Why?

- In textbooks, at least, the pH of a given solution is generally assumed as being between o and 14. Can it not be less than 0, or greater than 14? Why?

Finally, a suggestion: the code can be generalized to comprise weak bases and polifunctional acids and bases.     

Derivation of model equations

 

Before the equivalence point (0⋜ f(i) <1), we have to consider the following chemical equilibria (eq):

 

HA + H₂O ⇌ A^- + H₃O⁺ for which the acid ionization constant is defined:

 

Ka=[A^-]_eq [H₃O⁺]_eq/[HA]_eq (1)

 

and the water auto-ionization

 

H₂O + H₂O ⇌ H₃O⁺ + OH^- for which the ionic product constant is defined:

 

Kw=[H₃O⁺]_eq [OH^-]_eq (2)

 

As the base (NaOH, for example) is strong, it is totally ionized and the OH^-ions from it react with the H₃O⁺ions from the acid. The species electrically charged are A^- , H₃O⁺,OH^- and Na⁺. The total acid concentration in the mixture (AT, see Introduction) is:

 

AT = [HA]_eq + [A^-]_eq (3)

 

Additionally, the number of positive charges must be equal to the number of negative ones (electroneutrality condition), so:

 

BT + [H₃O⁺]_eq =[A^-]_eq + [OH^-]_eq (4)

 

where BT is the total base concentration in the mixture (see Introduction).

 

From equations (1), (2), (3) and (4), by simple algebraic manipulation, it is easy to eliminate all [...]_eq, excepting [H₃O⁺]_eq, leading to equation (BEP) of the Introduction:

 

[H₃O⁺]³ + (Ka+BT) * [H₃O⁺]² + (KA*BT - Ka*AT - Kw)*[H₃O⁺] - Ka*Kw = 0 (BEP)

 

As for the process at, and after the equivalence point (f(i) ⋝ 1), the salt (NaA), totally ionized, generally undergoes hydrolysis and the base in execess (NaOH) is also assumed completely ionized. Then, the chemical equilibria to be considered are:

 

A^_- + H₂O ⇌ HA + OH^-

 

for which the hydrolysis constant is defined:

 

Kh=[HA]_eq [OH-]_eq/[A-]_eq = Kw/Ka (5)

 

and, again, the water auto-ionization and respective ionic product constant.

 

Now, the chemical balances are:

 

ST=[A-]_eq + [HA]_eq (6)

 

and

 

BE+ST+[H3O+]_eq = [OH-]_eq + [A-]_eq (7)

 

being the last the electroneutrality condition. BE and ST (see Introduction) are, respectively, the concentration of the salt at the equivalence point and the concentration of the base in excess.

Subtracting equations (6) and (7):

 

[HA]_eq = [OH^-]_eq - [H₃O⁺]_eq - BE (8)

 

Now, eliminating all [...]_eq but [H₃O⁺]_eq from equations (2), (5), (7) and (8), leads to equation (EPAEP) of the Introduction:

 

[H₃O⁺]³ + (BE+ST+Ka) * [H₃O⁺]² - (KW-BE *Ka)*[H₃O⁺] - Ka*Kw = 0 (EPAEP)     

Method of successive bisections

 

In order to work out the roots of the continuous algebraic equations of the model by the bisection method, it is necessary to make an initial guess of the intervals of the hydrogen ion concentration, (X1,X2), where the roots can be found. In the present particular case, such a guess is made from the very physical conditions of the problem. Indeed, the only interesting roots are real and positive and are between well-defined limits.

 

The minimum of the interval, X1, is always X1=0 for there are no negative concentrations. As for he maximum of the interval, X2, before the equivalence point, a good guess is:

 

X2=AT + (Kw)^1/2

that corresponds to the virtual complete ionization of the acid, taking also into account the hydrogen ions from the water auto-ionization.

At, and after the equivalence point X2 is not greater than 10^{- 7} for the acid has been completely neutralized and the pH is between 7 ([H₃O⁺]=10^{- 7}) and ≈14 ([H₃O⁺]=10^{- 14}). So, a good guess is X2=10^{- 7}.

 

Once the initial interval is set up, its middle point is:

 

xm=(X1+X2)/2

 

Then, a search proceeds in order to determine the subinterval (X1,xm) or (xm,X2) where the root remains. This is done by the well-known theorem of mathematical analysis: "if a continous function f(x) has a unique root in the interval (x1,x2) then f(x1)*f(x2) < 0". Such result is intuitive: when the plot of a function intersepts the x-axis at a point (the root) the function changes its sign.

 

Now, if the root is in (X1,xm) then X2=xm; else X1=xm. The successive bisections go on until the lenght of the interval |X1-X2| is less than a pre-defined tolerance value where the iterations stop. Then, the root value is assumed to be (X1+X2)/2.     

Video

 Setting up and Performing a Titration by CarolinaBiological

 Version:

2. http://www.compadre.org/OSP/items/detail.cfm?ID=13410&Attached=1 original simulation by Fernando Silva Fernandes 

FAQ on Acid-Base Titrations and Simulations

1. What is the purpose of a titration, and how does this simulation model aid in understanding it? A titration is a laboratory technique used to determine the unknown concentration of a solution (the analyte) by reacting it with a solution of known concentration (the titrant). This simulation model helps visualize and understand the titration process, especially for monoprotic acids and monofunctional strong bases, by providing a virtual lab environment where users can observe the changes in pH and indicator color as the titration proceeds. The simulation removes some of the practical limitations of a physical lab and allows for more exploration of the variables involved.
2. How does the simulation determine the equivalence point, and why is it important? The equivalence point in a titration is the point where the moles of acid and base are stoichiometrically equivalent; they have completely neutralized each other. The simulation calculates this point based on the volumes and concentrations of the acid and base solutions by numerically solving complex mathematical equations. It also predicts the pH at the equivalence point by taking into account the acid ionization constant (Ka), which is not always 7 due to the hydrolysis of the salt produced in the reaction. Identifying the equivalence point is critical as it allows for accurate calculation of the unknown acid concentration.
3. How does the simulation choose an appropriate indicator for the titration? The simulation selects an indicator by comparing the pH of the solution at the equivalence point with the color change range of different indicators. The model contains a table of common indicators and matches the calculated equivalence point pH to an indicator whose range will be near the calculated value. This ensures that the color change of the indicator will coincide with the equivalence point and the end of the titration.
4. What are the key variables that users can manipulate within the simulation, and how do these changes affect the titration? Users can modify the acid ionization constant (Ka), the initial molar concentration of both the acid and the base, and the initial volume of the acid. Changing the Ka will determine how strong the acid is, impacting how it will react and its pH at equivalence. The acid and base concentrations, and the initial volume of the acid will impact the titration curve, where the equivalence point is reached, and will ultimately impact calculations for the concentration of the analyte.
5. The simulation uses numerical methods (bisection). What does this mean, and why is it necessary? The simulation numerically solves algebraic equations using the method of successive bisections, which involves iteratively narrowing the interval where a solution is located and calculating the midpoint until it is close enough. These equations, which determine the hydronium ion concentration, cannot be solved directly with a simple formula, making numerical methods necessary. In this way the simulation is able to accurately calculate pH and equivalence points.
6. What assumptions are made by this model, and why are they important to its functionality? The model assumes the acids are monoprotic (can donate one proton) and bases are monofunctional strong bases (fully ionize in water). These simplifications are necessary for the model's mathematical calculations. It also assumes that indicators are available to help identify the end point. The assumptions enable accurate modeling for a specific but significant portion of acid-base titrations.
7. Why does the simulation's derivation of the model equations consider both before and after the equivalence point, and what is the difference? The model considers different sets of equations before and after the equivalence point because the chemical equilibrium changes. Before the equivalence point, the solution contains mainly the monoprotic acid and its conjugate base and calculations are based on acid ionization and water auto-ionization. After the equivalence point, the solution contains the salt formed by the reaction, and excess base, requiring that the salt's hydrolysis, which is when water is split by the ions, be accounted for. The approach ensures the calculations consider the main chemical species at each stage for accurate predictions.
8. Can the simulation handle extremely weak or strong acids, and how is this achieved? The simulation can handle a wide range of acid strengths, from very weak to very strong, by allowing the user to input a wide variety of Ka values, and these values are plugged directly into the calculations of pH and equivalence point. The accuracy of the model, however, depends on numerical methods, which might face difficulties in extreme cases. Testing across a wide range of Ka values is important for model reliability, so feedback on inconsistencies is appreciated.