Translations

Code	Language		Translator	Run

Credits

Wolfgang Christian

http://iwant2study.org/lookangejss/06QuantumPhysics/ejss_model_BoundEigenstateSuperpositionwee/BoundEigenstateSuperpositionwee_Simulation.xhtml

Briefing Document: Bound Eigenstate Superposition Simulation

1. Overview

This document provides a briefing on the "Bound Eigenstate Superposition JavaScript HTML5 Applet Simulation Model" developed by Wolfgang Christian and hosted on the Open Educational Resources / Open Source Physics @ Singapore website. This interactive simulation is designed to help students and educators understand the principles of quantum mechanics, specifically the superposition principle and the behavior of wave functions.

2. Core Concept: The Superposition Principle

• Fundamental Building Blocks: The simulation is built upon the idea that in quantum mechanics, energy eigenfunctions (ψn(x)) and their corresponding energy eigenvalues (En) are fundamental. These are determined by a potential energy function V(x) and boundary conditions.
• Position Space: The energy eigenfunctions are primarily determined in position space.
• Superposition: More complex, time-dependent wave functions (Ψ(x,t)) can be constructed using the superposition principle. This principle states that a general quantum state can be expressed as a linear combination of energy eigenfunctions:
• Ψ(x,t) = Σ cn ψn(x) e^(-iEn t/ħ)
• where 'cn' are the expansion coefficients. The sum of the absolute squares of these coefficients equals one (Σ |cn|² = 1). This means that the sum of probabilities to be found in each quantum state must equal 1.
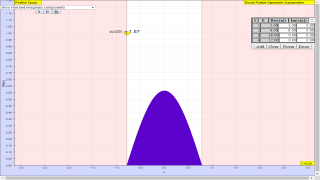
• Different States: The simulation demonstrates how different wave functions can be created by varying the number and values of the coefficients cn. These range from energy eigenstates (only one cn non-zero) to two-state superpositions and localized wave packets (many cn non-zero, like a Gaussian shape).
• Complete Orthonormal Set: Any complete orthonormal set of eigenfunctions can be used to construct the wave function Ψ(x,t).
• Simulation's Focus: The specific simulation focuses on demonstrating the time-dependent wave functions using either infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions.

3. Simulation Details & Features

• Platform: The simulation is an HTML5 applet designed to be accessible across various platforms, including: Android/iOS devices (phones/tablets/iPads), Windows/MacOSX/Linux (laptops/desktops), and ChromeBook Laptops.
• Embedding: The simulation can be embedded into other webpages using an iframe.
• Atomic Units: The simulation uses atomic units for calculation purposes. In these units, the reduced Planck constant (ħ), Bohr radius (a₀), and the mass of the electron (m) are set to unity. This is because calculations in quantum mechanics deal with very small or large values.
• One unit of time: 2.42×10⁻¹⁷ seconds
• One unit of distance: 5.29×10⁻¹¹ meters
• One unit of energy: 4.36×10⁻¹⁸ Joules
• Particle: The simulation models a particle with the mass of an electron using atomic units.
• Modeling Tool: The simulation was developed using the Easy Java/JavaScript Simulations (EjsS) modeling tool.

4. Learning Goals (As inferred from context)

The listed "Sample Learning Goals" (currently text) suggests the simulation aims to facilitate learning about:

• The concept of energy eigenfunctions.
• The superposition principle in quantum mechanics.
• The construction of wave functions.
• The behavior of wave packets.
• The differences between energy eigenstates, two-state superpositions, and localized wave packets.
• The use of atomic units in quantum mechanics.
• The visualization of time-dependent wave functions for different quantum systems.

5. Target Audience

• Students: Primarily targeted at Junior College level students studying quantum physics, but potentially useful for higher education as well.
• Educators: A valuable teaching tool for quantum mechanics concepts, offering interactive visual representation of abstract ideas.

6. Key Quotes

• "The fundamental building blocks of one-dimensional quantum mechanics are energy eigenfunctions ψn(x) and energy eigenvalues En."
• "Once these energy eigenstates are determined, more interesting quantum-mechanical wave functions Ψ(x,t) can be studied by applying the superposition principle"
• "Any complete orthonormal set of eigenfunctions can be used to construct the wave function Ψ(x,t)."
• "This simulation uses the superposition principle to construct and display a time-dependent wave function using either infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions."
• "In atomic units, one unit time is 2.42×10-17 seconds, one unit of distance is 5.29×10-11 meters, and one unit of energy is 4.36×10-18 Joules."

7. References

• A. P. French and E. F. Taylor: Qualitative plots of bound state wave functions, Am. J. Phys. 39, 961-962 (1971) - A good tutorial on the shape of energy eigenfunctions in relation to potential energy functions.
• David J. Griffiths: An Introduction to Quantum Mechanics (2ed) - A general reference for quantum mechanics with a relevant section on the topic of the simulation (page 28).

8. Related Resources

The webpage listing the simulation provides links to many other resources, including:

• Other physics simulations (covering topics like projectile motion, wave superposition, harmonic oscillators, etc.)
• Simulations related to other science topics such as chemistry and mathematics
• Links to modeling tools and authoring programs like EjsS
• Learning resources on conceptual instruction and modeling

9. Conclusion

The "Bound Eigenstate Superposition JavaScript HTML5 Applet Simulation Model" is a powerful interactive tool for visualising and understanding the superposition principle in quantum mechanics. Its use of atomic units, focus on either infinite square well or simple harmonic oscillator eigenstates, and the possibility to vary coefficients for creating different wave forms make it very useful for instruction. The simulation is also well embedded within a larger context of open-source educational resources for STEM subjects.

 

Quantum Mechanics: Bound Eigenstate Superposition Study Guide

Quiz

Instructions: Answer each question in 2-3 sentences.

1. What are the fundamental building blocks of one-dimensional quantum mechanics, and how are they related?
2. What is the superposition principle in the context of quantum mechanics?
3. How are the expansion coefficients (cn) related in the wave function and what does this mean?
4. What determines the specific form of a wave function in this context?
5. What two types of eigenfunctions can be used to create a time-dependent wave function in the simulation described?
6. Why are atomic units used instead of the metric system when calculating quantum mechanics phenomena?
7. What are the atomic units of time, distance and energy in this model?
8. What is the significance of the time-independent Schrodinger equation in this simulation?
9. What software tool was used to develop the simulation and how can you further investigate it?
10. Besides the superposition principle, what other concepts does this simulation model?

Quiz Answer Key

1. The fundamental building blocks are energy eigenfunctions (ψn(x)) and energy eigenvalues (En). Eigenfunctions represent possible states of a system, while eigenvalues represent the corresponding energy levels.
2. The superposition principle states that a quantum-mechanical wave function (Ψ(x,t)) can be represented as a sum of energy eigenfunctions, each multiplied by an expansion coefficient (cn). This means that a particle can exist in multiple states simultaneously.
3. The expansion coefficients (cn) satisfy Σ c n|2 = 1. This ensures that the total probability of finding the particle in any of its possible states is 1.
4. The form of the wave function is determined by the potential energy function V ( x ) , boundary conditions, and the specific combination of the expansion coefficients. Different coefficients create energy eigenstates, superpositions, or localized wave packets.
5. The simulation uses either infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions to construct and display a time-dependent wave function. These represent the energy states in different models.
6. Metric units are not well suited because quantum phenomena occur on microscopic scales with very fast timescales making values too large or too small for computation. Using atomic units simplifies the calculations.
7. In this model, one unit time is 2.42×10-17 seconds, one unit of distance is 5.29×10-11 meters, and one unit of energy is 4.36×10-18 Joules.
8. The time-independent Schrödinger equation determines the energy eigenfunctions and eigenvalues for a given potential, enabling the calculation of possible particle states within the simulation's system.
9. The simulation was developed using the Easy Java/JavaScript Simulations (EjsS) modeling tool. You can examine and modify the simulation by importing the model's zip archive into EjsS if you have version 5.2 or higher.
10. Besides the superposition principle, this simulation also models infinite square well and simple harmonic oscillator potentials, and provides a way to study the time-dependent behavior of wave functions using these concepts.

Essay Questions

Instructions: Answer each question in essay format.

1. Explain the significance of the superposition principle in quantum mechanics. Provide detailed reasoning and describe, in your own words, the conditions under which it applies using concepts from the source material.
2. Compare and contrast the use of metric units versus atomic units when modeling quantum phenomena. Discuss the advantages of using atomic units, relating to the specific quantities being calculated in this simulation.
3. Describe how the Bound Eigenstate Superposition simulation uses both the infinite square well and the simple harmonic oscillator potentials. Discuss the key differences between these potentials.
4. Elaborate on the role of energy eigenfunctions and energy eigenvalues in the simulation. How do they relate to the concept of a particle's state and energy?
5. Imagine you were tasked with improving the simulation. What key features would you add to make it more effective for students learning about quantum mechanics and the superposition principle? Discuss and justify your choices.

Glossary of Key Terms

Energy Eigenfunctions (ψn(x)): Specific solutions to the time-independent Schrödinger equation that represent possible states of a quantum system with definite energy. Also known as energy eigenstates.

Energy Eigenvalues (En): The specific values of energy associated with each corresponding energy eigenfunction. They represent the allowed energy levels for the system.

Superposition Principle: The principle that allows quantum systems to exist in a linear combination of multiple possible states simultaneously. This means the wave function can be expressed as a sum of energy eigenfunctions.

Expansion Coefficients (cn): Numbers that determine the amplitude and phase of each energy eigenfunction in the overall wave function. These coefficients determine the probability of measuring the particle in that specific state.

Time-Dependent Wave Function (Ψ(x,t)): The wave function that describes the quantum mechanical state of a particle, including how it evolves over time.

Infinite Square Well (ISW): A potential energy function that confines a particle to a region by imposing infinite potential barriers, meaning the particle cannot exist outside the region.

Simple Harmonic Oscillator (SHO): A model system describing a particle that experiences a restoring force proportional to its displacement from an equilibrium point, such as a mass on a spring.

Atomic Units: A system of units used in atomic and quantum physics, simplifying calculations by setting fundamental constants like the reduced Planck constant (ħ), Bohr radius (ao), and electron mass (m) to unity.

Schrödinger Equation: The fundamental equation of quantum mechanics that describes the evolution of a quantum system over time. The time-independent version is used to find the energy eigenfunctions and eigenvalues.

EjsS (Easy Java/JavaScript Simulations): A modeling tool used to develop interactive simulations, such as the one described in this resource, allowing users to examine and modify physics concepts.

 

Sample Learning Goals

[text]

For Teachers

The Superposition Principle

The fundamental building blocks of one-dimensional quantum mechanics are energy eigenfunctions ψ_n(x) and energy eigenvalues E_n. For a given potential energy function V(x) and boundary conditions, energy eigenfunctions can be determined either analytically or numerically. Most of the time in quantum mechanics these energy eigenfunctions are determined in position space. Once these energy eigenstates are determined, more interesting quantum-mechanical wave functions Ψ(x,t) can be studied by applying the superposition principle

where the expansion coefficients c_n satisfy Σ c_n|² = 1. Depending on how many of the coefficients c_n are non-zero, one may have an energy eigenstate, a two-state superposition, or even an initially localized (usually Gaussian shaped) wave packet.

Any complete orthonormal set of eigenfunctions can be used to construct the wave function Ψ(x,t). This simulation uses the superposition principle to construct and display a time-dependent wave function using either infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions.

Units

Although the metric (MKS) system of units has become the standard international system of units, it is not well suited for computation if the quantities being computed are very large or very small. Quantum phenomena occurs on the microscopic scale at very fast times and computations are usually done using an atomic system of units in which the reduced Plank's constant ħ, the Bohr radius a_o, and the mass of the electron m are set equal to unity. The one-dimensional time independent Schrödinger equation in these units is:

In atomic units, one unit time is 2.42×10^-17 seconds, one unit of distance is 5.29×10^-11 meters, and one unit of energy is 4.36×10^-18 Joules. This simulation models a particle with the mass of an electron using these atomic units.

References:

• For an excellent tutorial on energy eigenfunction shape and the relationship to the potential energy function, see: A. P. French and E. F. Taylor, Qualitative plots of bound state wave functions, Am. J. Phys. 39, 961-962 (1971).
• An Introduction to Quantum Mechanics (2ed) by David J. Griffiths page 28.

Credits:

The Bound Energy Eigenstate Superposition JavaScript simulation was developed by Wolfgang Chrsitian using the Easy Java/JavaScript Simulations (EjsS) modeling tool. You can examine and modify this simulation if you have EjsS version 5.2 or above installed by importing the model's zip archive into EjsS. Information about EjsS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.com/2016/06/bound-eigenstate-superposition-by.html 
2. http://www.compadre.org/osp/items/detail.cfm?ID=13742 original simulation by Wolfgang Christian

Other Resources

[text]

Frequently Asked Questions

1. What is the Superposition Principle in quantum mechanics?
2. The superposition principle states that any quantum mechanical wave function can be expressed as a sum of energy eigenfunctions. These energy eigenfunctions, denoted as ψn(x), are the fundamental building blocks of one-dimensional quantum mechanics and are associated with specific energy eigenvalues En. When combined, these eigenfunctions, through a process called superposition, can create more complex and interesting quantum mechanical wave functions Ψ(x,t). The weights of each eigenfunction in this sum are determined by expansion coefficients cn which must satisfy Σ|cn|² = 1.
3. What are energy eigenfunctions and energy eigenvalues?
4. Energy eigenfunctions (ψn(x)) are particular solutions to the time-independent Schrödinger equation for a given potential energy function V(x) and boundary conditions. Each eigenfunction corresponds to a specific, quantized energy level, called the energy eigenvalue (En). These eigenfunctions can be determined either through analytical calculations or numerical methods and are often found in position space. These states are time-independent, however, when superposed they can result in states that change over time.
5. What does the Bound Eigenstate Superposition JavaScript HTML5 Applet Simulation Model demonstrate?
6. This simulation demonstrates the superposition principle by constructing and displaying a time-dependent wave function using energy eigenfunctions. Specifically, it allows for the visualization of how different combinations of infinite square well (ISW) or simple harmonic oscillator (SHO) eigenfunctions create various wave patterns. By manipulating the expansion coefficients 'cn' one can observe the creation of energy eigenstates, two-state superpositions, or localized wave packets.
7. What are atomic units, and why are they used in this simulation?
8. Atomic units are a system of units in which certain fundamental physical constants are set equal to unity. Specifically, the reduced Planck's constant (ħ), the Bohr radius (ao), and the mass of the electron (m) are all set to 1. This system is used because quantum phenomena occur on very small scales and very fast times, making metric (MKS) units cumbersome for computations. In atomic units, one unit of time is 2.42×10−17 seconds, one unit of distance is 5.29×10−11 meters, and one unit of energy is 4.36×10−18 Joules.
9. What can I learn from this simulation about wave function behavior?

The simulation enables users to visualize how the superposition of energy eigenfunctions leads to a variety of wave function behaviors, including the formation of localized wave packets. It provides an understanding of how the system evolves over time based on the chosen eigenfunctions and their respective expansion coefficients. Users can see how these combinations result in wave functions that can change shape and move, rather than remaining in a stationary state.

1. What are the Infinite Square Well (ISW) and Simple Harmonic Oscillator (SHO) in the context of this simulation?
2. The simulation allows the use of eigenfunctions from either an infinite square well (ISW) or a simple harmonic oscillator (SHO) potential. The ISW potential confines a particle to a specific region of space while the SHO potential models a particle bound to a single point with a restoring force. These two are common and fundamental quantum mechanical systems that have analytically calculable eigenfunctions, making them excellent models to use when learning about the superposition principle.
3. How does the simulation use the expansion coefficients (cn)?
4. The expansion coefficients (cn) determine the contribution of each energy eigenfunction to the total wave function. Changing the values of these coefficients modifies the shape and time evolution of the resulting superposition. The sum of the squares of the magnitudes of these coefficients must always equal one (Σ |cn|²=1), reflecting the probability of finding the system in one of the energy eigenstates, and the overall normalization of the wave function.
5. Who developed this simulation and where can I learn more about the tools used?
6. The Bound Energy Eigenstate Superposition JavaScript simulation was developed by Wolfgang Christian using the Easy Java/JavaScript Simulations (EjsS) modeling tool. Information about EjsS can be found at: http://www.um.es/fem/Ejs/ and in the OSP ComPADRE collection at http://www.compadre.org/OSP/. You can modify the simulation further if you have EjsS version 5.2 or above installed by importing the model's zip archive into EjsS.