Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang; Loo Kang Wee

http://iwant2study.org/lookangejss/05electricitynmagnetism_22electromagneticinduction/ejss_model_ACgenerator07wee/ACgenerator07wee_Simulation.xhtml

Briefing Document: AC Generator Simulation Applet

1. Overview

This document reviews an interactive JavaScript HTML5 applet simulation model of an Alternating Current (AC) generator. The applet, developed by Boon Chien and hosted on Open Educational Resources / Open Source Physics @ Singapore, aims to demonstrate the principles of electromagnetic induction and how mechanical energy can be converted into electrical energy. This tool is designed to be accessible across various platforms including desktops, laptops, tablets and smartphones.

2. Core Concepts and Principles

• Electromagnetic Induction: The core principle behind the AC generator is electromagnetic induction. This is described as the phenomenon where "a wire passes through an external magnetic field, it causes electrons in that wire to move together in one direction". The interaction of the magnetic field created by the wire and the external magnetic field "results in a voltage (emf) to be 'induced' in the coil."
• Motional EMF: The motion of the electrons in the loop within the magnetic field is caused by "motional electromagnetic force (emf)".
• Alternating Current (AC): The generator produces AC because as the coil rotates, "it's moving across the magnetic field first in one direction and then in the other, which means that the flow of electrons keeps changing." This means "the electrons flow first in one direction and in the other", resulting in an alternating current.
• Faraday's Law: The induced electromotive force (emf) is governed by Faraday's Law, which states: "the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil." Mathematically: |ε| = | d( Φ)/ dt | where: * |ε| is the magnitude of the electromotive force (emf) in volts. * Φ is the magnetic flux through the circuit (in Weber). * N is the number of turns of wire in the loop.
• Lenz's Law: The direction of the induced current is defined by Lenz's Law, which states "an induced current is always in such a direction as to oppose the motion or change causing it." This means "the polarity of the induced emf is such that it produces a current whose magnetic field opposes the change which produces it".
• Magnetic Flux: The key to producing motional emf is "change in the magnetic flux experienced by the coil loop". Magnetic flux (Φ) is calculated by Φ = N.B.A cos ( B&A), where N is the number of loops of the coil, B is the magnetic field strength, A is the area of the coil and (B&A) is the angle between the magnetic field and the area of the coil.
• Relationship between Angular Velocity, Time, and Induced EMF: When the coil is spun at an angular frequency (ω) where θ = ω.t, the induced emf can be expressed as: ε = N.B.A d( sin ( θ )/ dt ) This equation is also expressed as: ε = N.B.A. ω .cos ( ω.t )
• Ohm's Law: When a closed circuit is connected to the rotating loop, Ohm's Law applies, linking voltage, current, and resistance: ε = N.B.A. d( sin ( θ )/ dt ) = I.R

3. Simulation Model Features

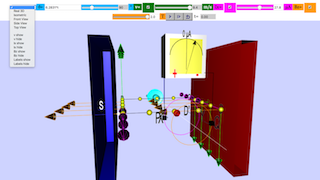
• Visual Representation: The simulation provides a 3D visualization of an AC generator, including magnets, a rotating coil (armature), slip rings, and carbon brushes.
• Interactive Controls: Users can interact with the model by:
• Rotating a handle bar to simulate the mechanical input.
• Adjusting the angle of the rotating handle via the input field θ(t).
• Altering simulation parameters via sliders:
• Bz: magnetic field strength
• Lengthx: length of coil
• Lengthz: width of coil
• N: number of turns of wire in the loop.
• R: resistance of the coil.
• Visualization of Current and Electron Flow: Checkboxes allow the user to visualize the direction of current flow and electron flow.
• Graphs: The simulation can display graphs of ε (induced emf) versus time (t), and Φ (magnetic flux) versus time (t), aiding the understanding of how these quantities change.
• Data Collection: Users are prompted to engage in activities that involve collecting data of θ (angle of rotation), Φ (magnetic flux), and induced emf (ε) to observe relationships and generate insights.
• Equation Representation: The model uses the equation getCurrent () = d( sin ( θ )/ dt ) and ε = N.B.A. d( sin ( θ )/ dt ) = I.R for simulations.

4. Learning Objectives

The applet is designed to achieve several learning goals, including:

• Understanding how electric generators convert mechanical energy into electrical power via electromagnetic induction.
• Visualizing the key components of an AC generator.
• Comprehending the relationship between motion, magnetic fields, and induced current.
• Exploring Faraday's Law and Lenz's Law in a practical context.
• Analyzing graphs of induced EMF and magnetic flux over time.
• Comprehending the difference between AC and DC current.
• Understanding the effect of varying parameters like magnetic field strength, number of turns in coil, and angular velocity on the induced EMF.

5. Pedagogical Approach

The applet promotes an inquiry-based learning approach through:

• Engage: Starting with a question about alternative energy sources to link the concept to real-world issues.
• Explore: Encouraging hands-on interaction with the simulation and guided experiments (e.g. changing values of simulation parameters).
• Evaluate: Prompting users to collect and analyze data, draw connections, and fill in tables with values and calculations.
• Elaborate: Providing text to assist learners to describe a simple form of a.c generator, to discuss forces, torques and to consider why certain factors do not affect the coil.

6. Key Activity Exercises

The simulation includes several activities and exercises:

• Exploration: Users are encouraged to explore the simulation, alter parameters, and observe the effects.
• Data Collection: Users are tasked with recording values of θ, Φ, and ε to observe the relationships between them.
• Analysis: Users are asked to interpret the graphs of ε vs t and Φ vs t and are also tasked with deducing the forces and torques acting on the coil.
• Conceptual Explanation: Users are prompted to explain phenomena like the direction of current flow, the concept of torque, and the change in flux linkage.
• Advanced Task: Advanced learners are prompted to create their own remix of the simulation and share it with the world.

7. Applications and Extensions

• Real-world Context: The applet is linked to discussions about global energy crises and alternative energy sources, highlighting the importance of generators.
• Teacher Support: The applet provides resources specifically aimed at educators to aid them in integrating the simulation in their teaching.
• Further Exploration: The page links to several other resources on similar topics, enabling deeper learning and investigation.

8. Key Quotes

• "Electric generators turn motion into alternating-current electric power by exploiting electromagnetic induction."
• "The key to producing motional emf is in change in the magnetic flux experienced by the coil loop."
• "Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil."
• "Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it."
• "ε = N.B.A. d( sin ( θ )/ dt ) = I.R"

9. Conclusion

The AC Generator JavaScript HTML5 applet is a valuable tool for teaching and learning about electromagnetic induction and AC generators. Its interactive nature, combined with clear visualizations and a structured pedagogical approach, make it effective for promoting conceptual understanding and critical thinking. The applet can also be integrated into discussions about renewable energy and real world applications of physics.

This document provides a comprehensive overview of the main themes and important aspects of the AC Generator simulation model. It should serve as a useful briefing for educators and learners interested in exploring this tool.

 

AC Generator Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the primary function of an AC generator?
2. Describe the basic structure of the AC generator discussed in the source material.
3. What is electromagnetic induction, and how does it contribute to the operation of an AC generator?
4. What is motional electromotive force (emf)?
5. Why is an alternating current (AC) produced in this type of generator?
6. Explain Faraday's Law of electromagnetic induction.
7. What is the significance of Lenz's Law in the context of AC generators?
8. Explain how the simulation models the relationship between the change in magnetic flux and the induced emf.
9. What are slip rings, and what is their function in the AC generator?
10. How can the user manipulate the simulation to affect the induced current?

Quiz Answer Key

1. An AC generator's primary function is to convert mechanical energy into electrical energy in the form of alternating current. It achieves this by exploiting the principles of electromagnetic induction.
2. The AC generator consists of two magnets that create a magnetic field, and a coil of wire (armature) that rotates within this field. The ends of the wire connect to slip rings and brushes, facilitating the flow of the generated current.
3. Electromagnetic induction is the phenomenon where a changing magnetic field induces an electromotive force (emf), which can drive an electric current. In an AC generator, it's the movement of the wire through the magnetic field that induces the current.
4. Motional emf is an electromotive force (voltage) induced in a conductor due to its motion through a magnetic field. This force causes electrons to move within the conductor, creating an electrical current.
5. An alternating current is produced because the coil is spinning through the magnetic field first in one direction and then in the other, which means that the flow of electrons keeps changing direction.
6. Faraday's law states that the induced emf in a coil is equal to the negative rate of change of magnetic flux multiplied by the number of turns in the coil. In essence, a changing magnetic flux creates a voltage.
7. Lenz's law states that the induced current always flows in such a direction as to oppose the change in magnetic flux that created it, providing the physical justification for the negative sign in Faraday’s Law.
8. The simulation models Faraday's law by demonstrating how the changing angle of the rotating loop within the magnetic field results in a changing magnetic flux, which then induces an electromotive force (emf) that drives the current.
9. Slip rings are conductive rings attached to the ends of the rotating coil of an AC generator. Their function is to provide continuous electrical contact with the brushes, allowing current to flow to an external circuit without tangling wires.
10. Users can manipulate the simulation through various controls, such as the handle's rotation speed (angular velocity) or by changing the magnetic field strength. Adjusting these parameters affects the rate of change of magnetic flux and thus the magnitude and frequency of the induced current.

Essay Questions

Instructions: Answer the following questions in a well-developed essay format.

1. Discuss the relationship between mechanical energy, electromagnetic induction, and the production of alternating current in an AC generator. Include in your response how this is modeled in the provided simulation.
2. Explain how Faraday's Law and Lenz's Law are interconnected and how they determine the magnitude and direction of the induced emf in the AC generator.
3. Analyze the factors that influence the magnitude of the induced emf in an AC generator, relating them to the mathematical equations and slider options presented in the simulation.
4. Describe the function of each component of the simulated AC generator (magnets, coil, slip rings, brushes) and the role each component plays in the energy conversion process.
5. Discuss the relevance of AC generators in the context of global energy production and suggest any potential advancements or modifications to improve the efficiency of AC generators.

Glossary of Key Terms

• Alternating Current (AC): Electric current that periodically reverses direction, unlike direct current (DC) which flows in one direction.
• Electromagnetic Induction: The process by which a changing magnetic field induces an electromotive force (emf) in a conductor.
• Electromotive Force (emf): The voltage or potential difference induced in a conductor, capable of driving electric current.
• Magnetic Flux: A measure of the total magnetic field passing through a given area.
• Faraday's Law: A law stating that the induced emf in a coil is proportional to the rate of change of magnetic flux through the coil.
• Lenz's Law: A law stating that the induced current always flows in such a direction as to oppose the change in magnetic flux that caused it.
• Armature: The rotating part of an electric generator, often consisting of coils of wire.
• Motional emf: An electromotive force (voltage) induced in a conductor due to its motion through a magnetic field.
• Slip Rings: Conductive rings attached to the rotating part of a generator that allow continuous current flow to the external circuit.
• Angular Velocity (ω): The rate at which an object rotates, measured in radians per second (rad/s).

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.acgeneratorapp214368&hl=en

Sample Learning Goals

 

Description

Electric generators turn motion into alternating-current electric power by exploiting electromagnetic induction. This AC generator consists of 2 pole magnets and a wire (usually a very long one that's wrapped to form several coils and known as an armature or coil). A hydraulic engine or some other outside source of motion (This applet has a handle bar for you to rotate) moves the wire or armature through the external magnetic field created by the magnets

When a wire passes through an external magnetic field, it causes electrons in that wire to move together in one direction. The current in the wire produce a magnetic field around the wire. The 2 different magnetic fields interact with each other results in a voltage (emf) to be "induced" in the coil. This motion of the electrons in the loop that is placed in a magnetic field is caused by a motional electromagnetic force (emf).

A simple alternating current (AC) generator is illustrated here. ABCD is mounted on an axle PQ. The ends of the wire of the loop are connected to 2 brushes contacting two slip rings continuously at position X & Y. Two carbon brushes are made to press lightly against the slip rings.

The key to producing motional emf is in change in the magnetic flux experienced by the coil loop.
In the case when an outside handle bar is rotating at θ (t) = 0.5*t, the coil is spinning at a constant rate of angular velocity ω = 0.5 rad/s within an external magnetic field. Because it is always moving through the magnetic field, a current is sustained but always varying. But, because the coil is spinning, it's moving across the magnetic field first in one direction and then in the other, which means that the flow of electrons keeps changing. Because the electrons flow first in one direction and in the other, the generator produces an alternating current.     

For Teachers

       Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. The induced electromotive force or emf, ε in any closed circuit is equal to the rate of change of the magnetic flux , Φ through the circuit.

|ε| = | d(Φ)/ dt  |

Where Φ = N.B.A cos ( B&A)

|ε|  is the magnitude of the electromotive force (emf) in volts

Φ is the magnetic flux through the circuit (in Weber).

N is the number of turns of wire in the loop

B is the magnetic field

A is area of coil

Angle B&A is the angle between vector magnetic field and vector perpendicular to the area

Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it.
The law provides a physical interpretation of the choice of sign in Faraday's law of induction, indicating that the induced emf and the change in flux have opposite signs. The the polarity of the induced emf is such that it produces a current whose magnetic field opposes the change which produces it

ε = - d(Φ)/ dt 

Apply Faraday's law and Lenz's law to the simulation model:

For the case of a rotating loop,

ε = - d(Φ)/ dt

From earlier equation as Φ = N.B.A cos ( B&A)

ε = - d(N.B.A cos ( B&A))/ dt

The physical setup of Bz and normal vector of area A when t = 0 s, such that angle B&A = ( θ + π/2 ).

And taking out the constants from the differential equation,ε = - N.B.A d( cos ( θ + π/2 )/ dt

From mathematical trigonometry identity, cos ( θ + π/2) = -sin ( θ  )

ε = - N.B.A d(-sin ( θ  )/ dt

To derive an expression for the induced emf across the slip rings when the coil is spun at an angular frequency, ω, knowing θ = ω.t 

ε = - N.B.A d(-sin ( ω.t  )/ dt )

ε = N.B.A d( sin ( θ )/ dt )     which the equation used by the custom function  getCurrent () = d( sin ( θ )/ dt )

When a closed circuit in connected to the rotating loop, using Ohm's law

ε =  N.B.A.d( sin ( θ )/ dt ) = I.R      which the equation used by the simulation model

When mechanical energy is used to rotate the loop, the armature induced an emf described by the right hand rule. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. 

Use the rotating handle function input field θ(t)= _________ to see what happens when the rotating handle cranks the loop in the Bz magnetic field. The checkbox current flow & electron flow allow different visualization since I = d(Q)/dt and Q= number of charge*e. The Play & Pause button allows freezing the 3D view for visualizing these induced currents and for checking for consistency with the right hand rule.

When the rotating handle is moved by the input field θ(t)= 2*t , induced current runs through ABCD (select the checkbox labels?) in a manner described by
ε =  N.B.A.ω .cos ( ω.t  ) = I.R.

Interpretation of graphs of ε versus t

If   θ(t)= 2*t , imply 2 =ω ε/R =  N.B.A.ω .cos ( ω.t  )/R = I. which is the modeled equation.

       If N = 1, B = 2 x10^-6 T, A = 1.5*1.5 m*m, R = 1 Ω

ε/R =  1.2.1.5*1.5.2x10^-6 .cos ( 2.t  )/1 = I.

ε = 9x10^-6 cos ( 2.t  ) = I

       Interpretation of graphs of Φ versus t

Since ε = - d(Φ)/ dt 

Therefore, 9x10^-6 cos ( 2.t  ) = - d(Φ)/ dt 

- ∫ 9x10^-6 cos ( 2.t  ).dt =  (Φ) 

-  4.5x10^-6 sin ( 2.t ) =  (Φ)

Activity Exercises

Engage:

Question: Given the context of global energy crisis, fossil fuel as primary source of energy and its effects of global warming, are you aware of any alterative energy source?

Possible student responses: Many students probably already know of clean energy and able to verbally mention some of them such as wind and wave energy.

 Answer: Yes! Wind energy and wave energy are examples of energy sources that convert mechanical sources of energy and convert it to electrical energy. Later, we will demonstrate a way to convert human mechanical energy in the form of rotating an axle to rotate a coil so as to get electrical energy. 

A real live demo is best.     

       Explore
1. Explore the simulation; this simulation is designed as an electric generator that turns motion into alternating-current electric power by exploiting electromagnetic induction. This AC generator model consists of 2 pole magnets and a wire (usually a very long one that's wrapped to form several coils and known as an armature or coil). A hydraulic engine or some other outside source of motion (This applet has a handle bar for you to rotate) moves the wire or armature through the external magnetic field created by the magnets.
2 The play button runs the simulation, click it again to pause and the reset button brings the simulation back to its original state.
3 by default values Bz, Lengthx, Lengthz, N, R, ϑ  = 6.2831*t  play the simulation. Notice ϑ  = 6.2831*t  is the angular displacement function of the handle bar. The wire is in a rotation motion and the galvanometer display the induced current in the AC generator. What is the physics principle simulated here.
Hint: Faraday's law
4 reset the simulation.
5 using the default values (Bz, Lengthx, Lengthz, N, R,), adjust the value of ϑ  = 1*t   play the simulation. What did you observe? Explain the motion in terms of the ϑ, ω
6 explore the slider Bz. what do this slider control?
7 explore the slider Lengthx. What does this slider control?

8 explore the slider Lengthz. What does this slider control?
9 together a variable called A is defined as Lengthx*Lengthz, suggest a suitable meaning for A.

10 by leaving the cursor on the slider, tips will appear to give a description of the slider. You can try it the following sliders such as the N, R, t, Φ , ε , i, v.
11 record down the names of the variables and its meaning from the tips.

9 there are some value of time of simulation t and the checkbox graph for height vs time.
10 vary the simulation and get a sense of what it does.

11 There is an external magnet with the poles as setup in the z axis direction.
What are the magnetic poles when Bz is positive?     

       12 What can you conclude about the directions of the magnetic field exerted by the magnets?

hint: the magnetic field vectors comes out from which pole when view from outside the magnet.     

       13 The external magnetic field Bz can be varied using the slider Bz. When Bz is positive, it is in the direction vertically up. Vary Bz until it is negative, what is the direction of the Bz then?     

       Evaluate:

14 Input into the input field θ(t) = __6.2832*t___
When θ = 0^o What is amount of magnetic flux Φ passing through the area of the coil loop is zero Wb.
15 Step the simulation by dt, take note of the new value of the θ and the new Φ reading. By calculating d(Φ)/ dt, at this instant in time. Think of a way, to collect the data to fill in the following table.

θ / deg.	t / s	Φ / Wb	d(Φ)/ dt / Wb/s	to be read from the graph ε  / V	i /   A
0
18
36
54
72
90
108
126
144
162
180
198
216
234
252
270
288
306
324
342

Select the Checkbox "Show Graph" and record down the value of the emf ε. Suggest a relationship between emf ε and the variables in the table. Collect more data to fill in the table if need.Elaborate:

16 The following passage (just an example) aims to aid learners describe a simple form of a.c. generator (rotating coil or rotating magnet) and the use of slip rings (where needed)When a coil is _______________ between the poles of the ___________, its wires cut through the _______________ causing an induced emf to be generate which causes a ____________ to flow if there is a closed electrical path circuit.
The _________ and ______________ of the induced current _____________ as the coil rotates. This is the basic principle behind the simple AC generator.(c) Sketch a graph of voltage output against time for a simple a.c. generator

 

 

 

 

 

 

Using default starting values of the simulation, play the simulation until at θ = 0 degree again at t > 0.0 s
What is the direction of the current flow in wire AB?

What is the direction of the current flow in wire CD?

using Fleming's left-hand rule, deduce the relative directions of force acting on

i)                    AB

ii)                   CD

iii)                 BC

iv)                 DA.

 Hint: note that F_mag = I*B*L*sin(I&B) may be useful.By taking moments about the axle PQ, consider the forces on AB and CD, deduce the direction of the torque T and the motion if the coil loop was initially at rest (ω = 0 deg/s). Select the suitable sliders of your choice and verify your hypothesis for 2 angles.

Discuss with your partner what you have discovered.

Ask your teacher if there are any problem/issues faced using this virtual lab.Explain and show the equations involving T ( in earlier part of question), why the forces on wire BC and DA did not contribute to the calculation of rotating torque about axle PQ?By considering the forces in the x direction for wire BC and DA, suggest what can happen to the coil loop if the forces are large enough.  Suggest why it does not happen in terms of the properties of the wires in the coil loop.Explain how a rotating coil in a magnetic field experiences a change in magnetic flux linkage and the induced emf.

What is the effect on the induced emf by increasing

(i)                  the number of turns on the coil, N

(ii)                the angular velocity, ω 

(iii)               the magnitude of the external Bz field.

After conducting some inquiry learning and examining the 3D view of the model on the virtual AC generator model discuss how this induced emf can be measured. You may right-click within a plot, and select "Open EJS Model" from the pop-up menu to examine the model equations of the motion. You must, of course, have EJS installed on your computer.Describe the action of the slip rings of the AC generator. Suggest the effect of adding a soft-iron cylinder in the winding the coil.Advanced Learner:
Please submit your remix model that model features that are not available in the existing virtual lab and share your model with the world through NTNUJAVA Virtual Physics Laboratory http://www.phy.ntnu.edu.tw/ntnujava/index.php?board=28.0. Impacting the world with your model now.     

Research

[text]

Video

 Version:

Other Resources

[text]

Frequently Asked Questions about AC Generators

1. How does an AC generator work to produce electricity?
2. An AC generator converts mechanical motion into electrical energy by utilizing the principle of electromagnetic induction. It consists of magnets, typically with two poles, and a wire coil (armature). When this coil is rotated within the magnetic field created by the magnets, the changing magnetic flux induces a voltage (electromotive force or emf) in the wire. This movement of electrons within the coil creates an electrical current. The key is the continuous change in magnetic flux as the coil spins, which results in an alternating current rather than a direct current.
3. What is meant by "magnetic flux" and why is it important for an AC generator?
4. Magnetic flux refers to the measure of the total magnetic field that passes through a given area. In an AC generator, the magnetic flux through the coil changes as the coil rotates. The induced emf, and therefore the current, is proportional to the rate of change of this magnetic flux. The constant changes in the direction and magnitude of this flux are the reason the generator produces alternating current. Specifically, the induced emf is equal to the negative rate of change of the magnetic flux multiplied by the number of turns of wire in the coil.
5. What is the role of slip rings and brushes in an AC generator?
6. Slip rings are metal rings that are fixed to the rotating coil and rotate with it. They are contacted by brushes, which are stationary conductors typically made of carbon. The slip rings and brushes provide a continuous electrical connection between the rotating coil and the external circuit, allowing the alternating current to flow out of the generator without the wires becoming tangled. This allows the electrons to maintain a current flow, as the induced flow is directly within the rotating loop.
7. How does the angle of the rotating coil affect the induced voltage (emf)?

The induced emf in the coil varies with the angle of the coil relative to the magnetic field. When the coil is perpendicular to the field, the rate of change of the magnetic flux is greatest, resulting in maximum induced emf. When the coil is parallel to the field, the rate of change of flux is zero, and therefore the induced emf is also zero. As the coil continues to rotate, the direction of the induced emf (and current) changes, leading to the alternating current nature of the output. The induced emf changes sinusoidally (it is a sine or cosine wave) with respect to time as the coil is rotated.

1. How do Faraday's Law and Lenz's Law relate to AC generator operation?
2. Faraday's Law of Induction states that the induced emf in a closed circuit is equal to the negative of the rate of change of magnetic flux through the circuit. This explains why the changing magnetic flux from the rotating coil produces an emf. Lenz's Law states that an induced current will flow in a direction that opposes the change that produces it. This ensures that the direction of the induced current produces a magnetic field that opposes the change in magnetic flux. This gives the induced current its polarity and ensures the induced current is sustained.
3. What factors affect the amount of voltage generated by an AC generator?
4. The amount of voltage generated is directly proportional to several factors, including: the number of turns of wire in the coil (N), the strength of the magnetic field (B), the area of the coil (A), and the angular velocity (ω) of the rotating coil. Specifically, the induced emf ε = N.B.A.ω.cos(ωt). Increasing any of these factors results in a higher induced voltage.
5. Why is it important to explore alternative energy sources, such as those that use AC generators?
6. Given global energy needs, and the negative environmental impact of burning fossil fuels, it is critical to explore alternative energy sources. These sources include solar, wind, and wave energy, all of which can utilize AC generators to convert mechanical energy into usable electricity. This is more sustainable than using fossil fuels, and could provide a way to reduce the effects of global warming.
7. How can the AC generator simulation described be used for learning?
8. The AC generator simulation allows users to explore the effects of altering various parameters, such as the magnetic field strength, the speed of rotation, and the coil's physical characteristics. This hands-on, virtual environment makes it easier to visualize the relationship between these variables and the resulting induced emf, and helps reinforce the understanding of the principles of electromagnetic induction. The simulation also allows users to look at graphical representations of the flux and induced emf to explore and analyze these relationships.