About
Topics
LightModeling for Snell's Law
Description
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light.In this Fermat Principle Model, the simulation shows the light path in the least possible time.
Sample Learning Goals
(c) recall and use the terms for refraction, including normal, angle of incidence and angle of refraction(d) recall and apply the relationship sin i / sin r = constant to new situations or to solve related problems
(e) define refractive index of a medium in terms of the ratio of speed of light in vacuum and in the medium
Activities
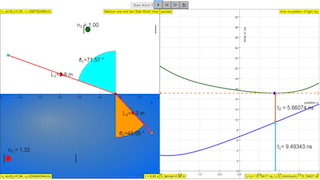
- Select the (drag and release the dots) desired position 1 and 2 of which light ray (RED) must be transmitted and received.
- Click run and the simulation will make the point of ray with the medium 1 and 2 interface, move and compute the following assuming point 1 (start TEAL color) and point 2 (end ORANGE color)
- L1=Math.sqrt((xc-x1)*(xc-x1)+(yc-y1)*(yc-y1))
- L2=Math.sqrt((xc-x2)*(xc-x2)+(yc-y2)*(yc-y2))
- time taken in medium 1, t1=n1*L1/c where n1 is refractive index of medium 1, c is speed of light
- time taken in medium 1, t2=n2*L2/c; where n2 is refractive index of medium
- using the evidences of t1 + t2 graph of ( time vs position x) , suggests what is the path that has the smallest travelling time, in other words the meaning of t1 + t2 is a minimum?
- using Snell's Law, verify if Fermat's principle is agreeable to Snell's Law?
- Calculate the error in the Snell's Law, n₁ sin(ϑ₁)=n₂ sin(ϑ₂) and Fermat's principle.
- Suggest a reason why the 2 answers are not exactly identical.
Version:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits


Fu-Kwun Hwang; lookang; tina
Briefing Document: 🔬Fermat Principle Refraction Simulation
1. Introduction
This document analyzes the provided resource, an online interactive simulation focusing on Fermat's Principle and its relation to the refraction of light. The simulation, built using JavaScript HTML5, is hosted by Open Educational Resources / Open Source Physics @ Singapore. This briefing will cover the core concepts, learning goals, interactive features and potential educational uses.
2. Core Concept: Fermat's Principle
The simulation is built around Fermat's Principle, a fundamental concept in optics. The resource states:
"In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light."
This principle implies that light, when traveling from one point to another, will follow the path that requires the least amount of time, not necessarily the shortest distance.
3. Simulation Description
- Interactive Model: The simulation allows users to manipulate the start (teal) and end (orange) points of a light ray passing through two mediums with different refractive indices.
- Visual Representation: The simulation displays the light ray's path and calculates the distances L1 and L2 in each medium using the following formulas:
- L1=Math.sqrt((xc-x1)*(xc-x1)+(yc-y1)*(yc-y1))
- L2=Math.sqrt((xc-x2)*(xc-x2)+(yc-y2)*(yc-y2))
- Time Calculation: The simulation then calculates the time taken in each medium based on refractive index and distance:
- time taken in medium 1, t1=n1*L1/c
- time taken in medium 1, t2=n2*L2/c where n1 and n2 are the refractive indices of medium 1 and 2 respectively, and c is the speed of light.
- Graph Visualization: The sum of these times (t1 + t2) is plotted on a graph against the position (x) of the point where the light ray crosses the interface between mediums.
- Minimum Time Path: The graph highlights the point where t1 + t2 is minimized, showing the path that a light ray would naturally follow.
4. Learning Goals
The simulation aims to help students:
- (c) Terminology: "recall and use the terms for refraction, including normal, angle of incidence and angle of refraction"
- (d) Snell's Law: "recall and apply the relationship sin i / sin r = constant to new situations or to solve related problems"
- (e) Refractive Index: "define refractive index of a medium in terms of the ratio of speed of light in vacuum and in the medium"
It also encourages users to:
- Compare Fermat's principle with Snell's Law and see how they are related.
- Calculate and identify any error in the two methods.
- Consider why the two answers might not be precisely identical.
5. Interactive Activities
The recommended activities within the simulation are:
- Position Adjustment: Users drag and drop start and end points for the light ray.
- Simulation Execution: Users click 'run', which initiates the calculation and visualization of the light path, times, and the graph of t1 + t2.
- Analysis and Comparison: Users observe the time graph to determine the path that produces the smallest travel time and therefore represents the path light will actually take. Then they should use Snell's Law and compare results. Finally, the user is to reconcile any difference in outcome.
6. Key Ideas and Facts
- Fermat's Principle and Least Time: The simulation demonstrably reinforces the idea that light travels along the path requiring the least time.
- Connection to Snell's Law: The simulation helps bridge the gap between the abstract principle of least time and the more commonly used Snell's Law, used in calculations concerning refraction. The model is set up to explore this relationship and identify any discrepancies.
- Refractive Index Impact: The time calculations in each medium highlight the role of refractive index in determining the light path.
- Error Analysis: The simulation introduces the concept that there may be slight differences in results between Fermat's Principle and Snell's Law, prompting users to investigate potential reasons for any discrepancies. The user is asked to "Suggest a reason why the 2 answers are not exactly identical."
- Visual and Interactive Learning: The interactive elements and the graphical visualization makes abstract physics principles accessible.
7. Potential Educational Uses
This simulation would be useful in:
- Physics Education: Teaching high school and junior college physics students about refraction and Fermat's Principle.
- Visualizing Abstract Concepts: Helping students visualize abstract concepts like the path of light, time of travel, and the impact of refractive index.
- Bridging Theory and Practice: Connecting abstract theoretical frameworks (Fermat's Principle) with commonly used practical calculations (Snell's Law).
- Inquiry-Based Learning: Providing an opportunity for students to investigate and explore the reasons behind the observed behavior of light.
8. Technical Details
- Platform: JavaScript HTML5, making it accessible on various devices (desktops, laptops, tablets, smartphones) via a web browser.
- Embedded Model: The simulation can be embedded into other websites using an iframe.
- Open Source: The source code is readily available for modification and reuse.
9. Additional Resources
The document also lists a comprehensive set of "Other Resources," which points to many other simulations related to physics and math. These may be useful in planning broader classroom activities.
10. Conclusion
The Fermat's Principle simulation is a valuable and effective educational tool. It visually demonstrates the core concept and links it to related ideas such as Snell's law. The simulations interactivity gives a hands-on means of exploration. The use of the graph to demonstrate how the light's path is influenced by minimal travel time is a particularly strong feature of the simulation. Its availability on multiple platforms and open-source nature enhance its accessibility and potential impact.
Fermat's Principle of Least Time: A Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- What is Fermat's Principle, and how does it define the path of light?
- In the simulation, what are the roles of points 1 (TEAL) and 2 (ORANGE), and what do L1 and L2 represent?
- How do the values t1 and t2 relate to the refractive indices (n1 and n2) of the mediums and the speed of light (c)?
- What is the relationship between the t1 + t2 graph and the path with the smallest traveling time according to Fermat’s Principle?
- What is Snell's Law, and what is the constant relationship it describes?
- How can the simulation be used to test the agreement between Fermat’s principle and Snell's Law?
- According to the description of the simulation, how is the "error" in the calculation of Snell's Law related to the Fermat's principle?
- What are the key terms associated with refraction, and what does each of them represent?
- What does the refractive index of a medium measure?
- How is the JavaScript simulation platform described in this source used in education and what does it allow students to do?
Answer Key
- Fermat's Principle states that light travels between two points along the path that takes the least amount of time. This principle can be considered as the definition of a ray of light, suggesting that light always follows the most efficient route in terms of time.
- Point 1 (TEAL) is the starting point of the light ray, and Point 2 (ORANGE) is the ending point. L1 represents the distance the light ray travels in medium 1, and L2 represents the distance it travels in medium 2.
- t1 is the time taken for light to travel through medium 1, calculated as n1 * L1 / c, where n1 is the refractive index of medium 1 and c is the speed of light. Similarly, t2 is the time taken in medium 2, calculated as n2 * L2 / c using corresponding refractive index and length.
- The t1 + t2 graph, which plots time versus position, shows that the minimum point on the graph corresponds to the light path that requires the smallest travel time, supporting Fermat’s principle. Light travels along the path of least time.
- Snell's Law describes the relationship between the angles of incidence and refraction when light passes between two different mediums, where the ratio sin i / sin r equals a constant value for given mediums. It states that n₁ sin(ϑ₁)=n₂ sin(ϑ₂).
- The simulation allows users to adjust the points and observe how the light path changes, allowing a comparison between the path that corresponds to Fermat's principle of least time with that calculated using Snell's Law to verify agreement.
- The simulation calculates the path using both Fermat’s principle and Snell's Law, and can measure and show if there is any difference between the results of each. It asks users to think why the answers are not identical.
- The key terms for refraction are normal, angle of incidence, and angle of refraction. The normal is a line perpendicular to the interface; the angle of incidence is the angle between the incident ray and the normal; and the angle of refraction is the angle between the refracted ray and the normal.
- The refractive index of a medium is a measure of how much light slows down when traveling through it. It is defined as the ratio of the speed of light in a vacuum to the speed of light in that medium.
- The JavaScript simulation platform is used to create interactive models that allows students to visualize and investigate physics phenomena, in this case light refraction. The simulation supports hands-on learning that reinforces concepts, calculations, and applications of physics principles.
Essay Questions
Instructions: Answer each of the following questions in essay format. Your response should demonstrate a thorough understanding of Fermat's Principle, Snell's Law, and the simulation tool presented in the provided source.
- Discuss how Fermat's Principle of Least Time provides a fundamental explanation for the behavior of light as it travels through different mediums, and how it relates to the concepts of incidence and refraction.
- Explain how the JavaScript simulation model demonstrates Fermat's Principle and how it can be used to explore and understand the relationship between Snell's Law and the principle of least time.
- Describe the key mathematical calculations and their significance within the simulation. How do these calculations validate both Fermat's Principle and Snell’s Law?
- Analyze the potential discrepancies between the predictions of Fermat’s Principle and Snell’s Law within the simulation. Why might the simulation indicate that these two might not be in complete agreement, and how could this help improve physics education?
- Evaluate the educational benefits of using interactive simulations like the Fermat's Principle model. Consider the ways it enhances understanding of abstract physics concepts, and how it is useful for scientific inquiry.
Glossary
Angle of Incidence: The angle between the incident light ray and the normal (a line perpendicular to the surface) at the point of incidence.
Angle of Refraction: The angle between the refracted light ray and the normal at the point of refraction.
Fermat's Principle: The principle stating that light travels between two points along the path that takes the least time.
Medium: A substance or material through which light can travel.
Normal: A line perpendicular to the interface between two mediums at the point where the light ray intersects.
Refraction: The bending of light as it passes from one medium to another due to a change in speed.
Refractive Index: A measure of how much light is slowed down when traveling through a medium; the ratio of the speed of light in a vacuum to the speed of light in that medium.
Snell's Law: A law describing the relationship between the angles of incidence and refraction when light passes between two different mediums, expressed as n₁ sin(ϑ₁) = n₂ sin(ϑ₂).
Speed of Light (c): The speed at which light travels in a vacuum, approximately 299,792,458 meters per second.
JavaScript Simulation: A program written in JavaScript, designed to simulate a physical or mathematical model for educational purposes.
Versions
- http://weelookang.blogspot.sg/2015/07/ejss-fermats-principle-refraction-model.html JavaScript version of Fermat's principle by Fu-Kwun Hwang and Loo Kang Wee
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2494.0 Java version of Fermat's principle by Fu-Kwun Hwang
Other Resources
FAQ: Fermat's Principle and Refraction
- What is Fermat's Principle? Fermat's Principle, also known as the principle of least time, states that light travels between two points along the path that takes the least amount of time. This principle is foundational in optics and can be used to explain the path of light. It essentially defines a ray of light as following the quickest possible route.
- How does the simulation model demonstrate Fermat's Principle? The simulation visually demonstrates Fermat's Principle by allowing users to set start (teal) and end (orange) points for a light ray. The simulation then calculates various paths the light could take, specifically the path with a point of refraction where the light ray bends as it enters a new medium. It computes the total time taken by the light to travel along each of these paths (t1+t2) and demonstrates how the actual light ray follows the path that results in the minimum time. This is done graphically, showing a curve of time vs a changing position of the refraction point, the minimum of this curve shows the shortest time the light ray needs.
- What is the relationship between Fermat's Principle and Snell's Law? Fermat's Principle, which dictates that light takes the path of least time, can actually be used to derive Snell's Law. Snell's law, expressed as n₁ sin(ϑ₁) = n₂ sin(ϑ₂) describes the relationship between the angles of incidence and refraction at an interface between two different media (where n represents the refractive index of each medium). The simulation allows users to verify if the calculated path from Fermat's Principle matches the prediction of Snell's Law. It allows the student to "test what you've learned" about Snell's Law by comparing it to Fermat's principle.
- How does the simulation calculate the time taken by light in different mediums? The simulation calculates the time taken by light to travel through each medium using the following formulas:
- L1 = Math.sqrt((xc-x1)*(xc-x1)+(yc-y1)*(yc-y1)) (distance in medium 1)
- L2 = Math.sqrt((xc-x2)*(xc-x2)+(yc-y2)*(yc-y2)) (distance in medium 2)
- t1 = n1*L1/c (time in medium 1)
- t2 = n2*L2/c (time in medium 2) Where (x1, y1) and (x2, y2) are the start and end points respectively, (xc, yc) is the point of refraction on the interface between media, n1 and n2 are the refractive indices of the respective mediums, and c is the speed of light. These equations enable computation of total time t1+t2.
- What do the terms "angle of incidence" and "angle of refraction" mean, in the context of refraction? The angle of incidence (ϑ₁) is the angle between the incoming light ray and the normal (a line perpendicular to the surface) at the point where the light ray meets the interface between two mediums. The angle of refraction (ϑ₂) is the angle between the refracted (bent) light ray and the normal on the other side of the interface. The normal is just a reference line.
- What is refractive index, and how is it defined in the simulation? The refractive index of a medium (n) is a measure of how much light is slowed down when traveling through that medium compared to a vacuum. The simulation uses the relationship that defines the refractive index as n = c/v where c is the speed of light in a vacuum and v is the speed of light in the medium, in addition to how it affects the calculation of the time t1 and t2.
- Why might there be slight errors when comparing Fermat's Principle calculations to Snell's Law in the simulation? The simulation uses numerical computations to approximate the path that takes the least time, there may be slight errors due to limitations in computer precision or approximations in the calculation. These approximations make it difficult to find the exact minimum point, whereas Snell's law gives us a perfect equation for the same scenario. The simulation highlights the concept that, while Fermat's principle explains the physical phenomena, it's not necessarily about perfect precision, and numerical methods are required to find the actual minimum.
- What can students learn from this simulation? Students can learn core concepts about light, including: - The definition of Fermat's Principle and its significance in optics - The nature of refraction and the related terms, like angle of incidence and refraction - The application of Snell's Law in calculating refractive light paths - The relationship between refractive indices and light speed - To explore through an interactive simulation the fundamental idea that light follows a least time path - The idea that numerical computations may involve small approximations and errors. - This allows a student to visualize and interact with abstract concepts in a more tangible way and promote understanding.