About

Topics

Progressive waves
Transverse and longitudinal waves
Determination of frequency and wavelength
Stationary waves

Description

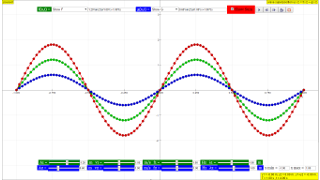
Play with the 2 Wave Superposition Model. Test what you've learned by exploring the amplitudes, wave velocities, frequencies, wavelengths.

As a pedagogical tool, "modeling pedagogy: key in your own equation like A*sin(2*pi/λ(x-v*t) form" .

for ease of keying in, select from the dropdown menu is also possible before adding on through the input fields of f(x) and g(x).

The One-Dimensional Wave Function Superposition JavaScript Model shows how the superposition principle gives rise to wave phenomena such as standing waves and beats. Users enter real-valued wave functions and observe both the time dependent functions and their superposition. This model uses the JavaScript mathematical function parser.

Sample Learning Goals

(a) show an understanding and use the terms displacement, amplitude, phase difference, period,
frequency, wavelength and speed
(b) deduce, from the definitions of speed, frequency and wavelength, the equation v = fλ
(c) recall and use the equation v = fλ
(f) analyse and interpret graphical representations of transverse and longitudinal waves
(a) explain and use the principle of superposition in simple applications

Version:

1. http://weelookang.blogspot.sg/2013/12/ejss-wave-1d-superposition-model.html

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; wolfgang, This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/04waves_11superposition/ejss_model_wave1d01/wave1d01_Simulation.xhtml

Briefing Document: Wave Superposition JavaScript HTML5 Applet Simulation Model

1. Introduction

This document analyzes the "Wave Superposition JavaScript HTML5 Applet Simulation Model" resource from Open Educational Resources / Open Source Physics @ Singapore. This resource is an interactive simulation designed to help learners understand the principle of wave superposition and its consequences.

2. Main Themes and Key Concepts

• Wave Superposition: The core focus of the simulation is the principle of superposition, which states that when two or more waves overlap, the resulting displacement at any point is the sum of the individual displacements. The simulation visually demonstrates this principle.
• Wave Properties: The simulation allows users to explore fundamental wave properties, including:
• Displacement: The distance a point on a wave is moved from its equilibrium position.
• Amplitude: The maximum displacement of a wave from its equilibrium position.
• Phase Difference: The difference in the phase (position in the cycle) between two or more waves.
• Period: The time taken for one complete cycle of a wave.
• Frequency: The number of wave cycles per unit time.
• Wavelength: The distance between two successive crests or troughs of a wave.
• Speed: The rate at which a wave travels through a medium.
• Wave Types: The resource implicitly covers both transverse and longitudinal waves, as evidenced by the mention in the "Topics" section.
• Standing Waves and Beats: The description notes that the model demonstrates how superposition gives rise to phenomena such as standing waves (formed by interference of waves) and beats (periodic variations in amplitude due to superposition of waves of slightly different frequencies).
• Mathematical Modeling: The simulation encourages "modeling pedagogy," allowing users to input their own wave equations in the form of A*sin(2*pi/λ(x-v*t). It also offers a user-friendly dropdown menu for quick function selection. This promotes a deeper understanding by bridging the gap between abstract mathematical representations and concrete visualisations.

3. Simulation Description and Features

• Interactive and Exploratory: The simulation is designed for active learning. It allows users to "play with" the parameters, testing how changes to amplitudes, velocities, frequencies, and wavelengths affect the resultant wave.
• JavaScript-Based: This is a JavaScript simulation meaning it can run directly in web browsers across different devices such as laptops, desktops, tablets, and smartphones without needing a Java Plugin.
• Function Parser: The model uses a JavaScript mathematical function parser, which allows users to directly input wave functions to explore various combinations.
• Visualization: The simulation visually represents both the individual waves and their superposition, aiding in comprehension.

4. Pedagogical Goals and Learning Outcomes

The simulation is designed to support the following learning goals:

• (a) Terminology: Students should understand and be able to use key wave terms like displacement, amplitude, phase difference, period, frequency, wavelength and speed.
• (b) Relationship between speed, frequency and wavelength: Learners should be able to deduce the relationship between wave speed, frequency, and wavelength, leading to the equation v = fλ.
• (c) Using the Wave Speed Equation: Learners should be able to apply the equation v = fλ in problem-solving.
• (f) Graphical Analysis: Learners should be able to analyze and interpret graphical representations of transverse and longitudinal waves.
• (a) Superposition Principle: Learners should be able to explain and use the principle of superposition in simple scenarios.

5. Supporting Resources

The resource provides a list of related simulations and tools, including:

• JavaScript simulations by Andrew Duffy: These simulations cover specific wave phenomena like beats, interference of pulses, and general interference.
• Java simulations by Fu-Kwun Hwang: These simulations focus on the superposition of two waves with different phases, amplitudes, and directions, further reinforcing and extending understanding.
• Desmos and GeoGebra links: These links provide interactive graphing tools and models, offering alternative ways to visualize wave superposition.

6. Technical Details and Credits

• Development Credits: The primary author for the model is Wolfgang Christian, and the contact email is provided.
• Related Work: The simulation is based on the Physlet Sound Illustrations Package and is linked to Physlet Physics Chapter 18.
• License: The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License. The EasyJavaScriptSimulations Library has specific usage terms.

7. Supporting Educational Resources

The website provides a wide variety of interactive models and simulations spanning various topics in physics, chemistry, and math. Here are a few that stood out in the attached text:

• Kinematics or Moving Car 1D Model with Tracker Related Kinematics Modeling Capability JavaScript HTML5 Applet Simulation Model
• 🔊Doppler Effect Sound Wave JavaScript HTML5 Applet Simulation Model
• ⚽Secondary Projectile Motion Energy Model
• ⚛️Photoelectric Effect JavaScript HTML5 Applet Simulation Model
• 🌊EJS Ripple Tank Model
• 🔬 Single Slit Diffraction JavaScript HTML5 Applet Simulation Model
• Double Slit Diffraction Model HTML5 Applet Javascript
• 🧲EJS Lorentz Force 3D Java Applet Simulation Model
• 🚀Rocket JavaScript HTML5 Applet Simulation Model
• Rutherford's Atomic and Thomson's Configurable Plum Atomic-Model JavaScript HTML5 Applet Simulation Model
• Tracker Bungee Jumping Tiger Fox by Leong Tze Kwang, Lim Jia Hui
• Pressure by PhET
• Sound Wave Longitudinal Wave JavaScript HTML5 Applet Simulation Model

8. Conclusion

The "Wave Superposition JavaScript HTML5 Applet Simulation Model" is a valuable educational tool. Its interactive nature, coupled with the ability to manipulate wave parameters and input custom equations, promotes a deeper understanding of wave superposition. The resource's emphasis on linking mathematical concepts to visual representations makes it an excellent tool for both in-class learning and self-directed study, as well as the number of other physics models the site hosts. The additional resources provided on the site expand the scope of learning and provide valuable additional models on many topics. The website is an incredible resource for interactive educational tools.

 

Wave Superposition Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the principle of superposition in the context of waves?
2. What are some examples of wave phenomena that can be explained by the superposition principle?
3. What are the primary variables you can manipulate using the provided wave superposition model?
4. What does the term "displacement" mean in the context of a wave?
5. How do you determine the speed of a wave if you know its frequency and wavelength?
6. What is the difference between a transverse and longitudinal wave?
7. How can you visually identify a standing wave in a superposition of waves?
8. What is the role of the "JavaScript mathematical function parser" in the wave superposition model?
9. What types of devices can the simulation be used on?
10. How does the simulation support "modeling pedagogy"?

Quiz Answer Key

1. The principle of superposition states that when two or more waves overlap, the resulting displacement at any point is the vector sum of the displacements of the individual waves. This means the waves pass through each other unaffected, and their amplitudes add (or subtract).
2. Examples include standing waves, beats, and interference patterns, all of which result from the combination of two or more waves. Superposition is a core principle in understanding how these wave phenomena emerge.
3. Using the model, you can manipulate the amplitudes, wave velocities, frequencies, and wavelengths of the individual waves. The model allows for exploring how different combinations affect the resulting wave.
4. Displacement refers to the distance a particle in the medium is moved from its equilibrium position due to the passage of the wave. It can be either positive or negative, indicating the direction of the movement.
5. The speed of a wave is the product of its frequency and wavelength, expressed by the equation v = fλ. This equation is derived from the definitions of speed, frequency, and wavelength.
6. In a transverse wave, the oscillations are perpendicular to the direction of the wave's propagation, while in a longitudinal wave, the oscillations are parallel to the wave's direction. Sound waves are an example of longitudinal, and light waves are transverse.
7. Standing waves appear as fixed patterns with nodes and antinodes, where the wave seems to be vibrating in place rather than propagating forward. Nodes are points of zero displacement, while antinodes are points of maximum displacement.
8. The JavaScript mathematical function parser allows users to input real-valued mathematical equations that define the wave functions. It interprets these equations to generate the visuals, and it adds real time responsiveness to the model.
9. The simulation is designed to be used on a variety of devices, including laptops, desktops, Chromebooks, Android/iOS devices such as phones, tablets and iPads.
10. The simulation allows users to input their own wave function equations, helping them explore how different parameters affect the results. The ability to test equations is an important aspect of the modeling pedagogy approach.

Essay Questions

Instructions: Answer the following essay questions thoroughly, using examples from the provided text.

1. Explain how the wave superposition model can be used to demonstrate the formation of standing waves, including a discussion of the parameters that influence their characteristics.
2. Describe the relationship between frequency, wavelength, and speed of a wave, and explain how this relationship is incorporated in the simulation.
3. Discuss the pedagogical value of using interactive simulations like the wave superposition model in learning about wave phenomena, relating it to the "modeling pedagogy" mentioned in the text.
4. Analyze how the JavaScript-based model can help both visualize and understand the principle of superposition, referencing its key interactive features and flexibility for users.
5. Compare and contrast the various resources provided (e.g., other simulations, Desmos models) to explore wave superposition, and explain how using multiple modalities can improve learning.

Glossary

• Amplitude: The maximum displacement of a wave from its equilibrium position.
• Displacement: The distance a particle in a medium is moved from its equilibrium position due to the passage of a wave.
• Frequency: The number of complete wave cycles that pass a given point in one second, measured in Hertz (Hz).
• Longitudinal Wave: A wave in which the oscillations are parallel to the direction of wave propagation.
• Modeling Pedagogy: An educational approach that emphasizes the use of models, like simulations, for learning, allowing students to actively explore concepts by manipulating parameters.
• Nodes: Points along a standing wave where the displacement is always zero.
• Phase Difference: The difference in the phase of two or more waves, determining their relative positions.
• Principle of Superposition: When two or more waves overlap, the resulting displacement at any point is the vector sum of the displacements of the individual waves.
• Standing Wave: A wave pattern formed by the interference of two waves traveling in opposite directions. Characterized by fixed nodes and antinodes.
• Transverse Wave: A wave in which the oscillations are perpendicular to the direction of wave propagation.
• Velocity (wave): The speed at which the wave propagates through the medium, typically represented by v.
• Wavelength: The distance between two consecutive points on a wave that are in phase (e.g., two crests or two troughs), typically represented by λ.

Versions

2. http://www.opensourcephysics.org/items/detail.cfm?ID=13307 Physlet Sound Illustrations Package Physlet Physics Chapter 18

   
   

Other Resources

1. http://physics.bu.edu/~duffy/HTML5/wave.htmlJavaScript version by Andrew Duffy
2. http://physics.bu.edu/~duffy/HTML5/beats.htmlJavaScript version by Andrew Duffy
3. http://physics.bu.edu/~duffy/HTML5/interference_of_pulses.htmlJavaScript version by Andrew Duffy
4. http://physics.bu.edu/~duffy/HTML5/interference.html JavaScript version by Andrew Duffy
5. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=829.0 Java version Superposition of Two Waves (with different phases,same amplitude,frequency) by Fu-Kwun Hwang
6. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=752.0 Java version Superposition of two waves (same frequency, different amplitude, phase/dir ) by Fu-Kwun Hwang
7. https://www.desmos.com/calculator/65ycbghqli 
8. https://www.desmos.com/calculator/bstgkcmdvp from tat leong
9. https://www.geogebra.org/m/z57naxTr by ukukuku 

FAQ: Wave Superposition and Simulation Tools

1. What is wave superposition, and why is it important to study? Wave superposition is a principle that states that when two or more waves overlap in space, the resulting displacement at any point is the sum of the individual displacements of each wave. This principle is fundamental in understanding a wide range of wave phenomena, including interference, standing waves, and beats. Understanding superposition allows us to analyze and predict how waves interact and create complex patterns, which is crucial in fields like optics, acoustics, and quantum mechanics.
2. What concepts can be explored using the Wave Superposition JavaScript HTML5 Applet Simulation Model? This simulation model allows users to investigate several key wave properties including displacement, amplitude, phase difference, period, frequency, wavelength, and wave speed. Users can also explore the relationship between speed, frequency, and wavelength, and observe how the principle of superposition gives rise to phenomena such as standing waves and beats. Furthermore, it allows the use of custom wave functions as inputs, allowing the user to directly test the effects of these parameters.
3. How does the simulation model allow users to input and manipulate waves? The simulation model offers two main ways to input wave functions: users can select from a dropdown menu of pre-defined functions and also directly input their own equations in the form of A*sin(2*pi/λ(x-v*t). This flexibility allows users to explore simple waves or more complex custom-defined waves, making it a robust pedagogical tool. The model uses a JavaScript mathematical function parser to evaluate these functions, ensuring accurate simulations.
4. What are some real-world phenomena that can be explained by the principle of superposition? The principle of superposition can be used to understand a diverse range of phenomena. Examples include the creation of standing waves in musical instruments, the phenomenon of beats when two slightly different frequencies are sounded together, the interference patterns created by light waves in double-slit experiments, and the behavior of radio waves that combine to create coverage patterns for communications, amongst others. These simulations help to make these abstract phenomena more intuitive through dynamic visualizations.
5. What types of waves can be explored using the simulation model? The model specifically mentions the exploration of progressive waves, transverse waves, and longitudinal waves. This implies that it can be used to explore various types of wave motion. The description of the applet focuses on superposition of general waves, making it applicable to both mechanical and other types of wave phenomena that demonstrate the property of superposition.
6. Who developed this simulation, and what other resources are available? The simulation is part of the Open Educational Resources / Open Source Physics @ Singapore initiative. The original code was written by Wolfgang Christian, with the Java version built by Fu-Kwun Hwang. Links to related simulations created by Andrew Duffy are also provided, offering alternative perspectives on wave phenomena. The resource page includes various translations, versions and related resources from other institutions and individuals.
7. Besides wave superposition, what other topics are available within this resource? This platform provides a broad range of interactive simulations and learning tools covering a wide variety of physics and mathematics concepts. These include topics like kinematics, projectile motion, energy, circular motion, gravity, optics, electromagnetism, nuclear physics, and much more. There are also several simulations related to modeling using tracker software and also educational modeling using EJS. These tools facilitate hands-on learning and help in visualizing complex phenomena, spanning introductory to advanced topics.
8. Is this resource available for different devices and platforms? Yes, this resource and the specific wave superposition model are designed to be accessible on various devices including desktops, laptops, Chromebooks, and mobile devices (Android/iOS, including phones and tablets). This is made possible by using JavaScript and HTML5, which ensures compatibility across multiple platforms without the need for specific plug-ins or software installs. The simulation can also be embedded into other websites using provided iframe code.