About

Multiple Slit Diffraction

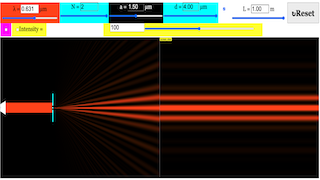
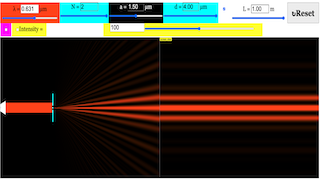
The EJS Multiple Slit Diffraction model allows the user to simulate Fraunhofer diffraction through single or multiple slits. The user can modify the number of slits, the slit width, the slit separation and the wavelength of the incident light. The scale of the diffraction pattern can also be changed and a plot of the light intensity can be toggled on and off with a checkbox.

 

The minima of single slit diffraction are determined by:

where D is the single slit width. For double slit interference, constructive interference (bright spots) are found at:

and destructive interference dark spots are located at:

where d is the distance between slits.

Multiple slits will sharpen (narrow) the regions of constructive interference.  The overall pattern from multiple slits will be the two-slit pattern multiplied by the single slit diffraction envelope.

References:

• Douglas Giancoli, Physics: Principles with Applications sixth edition, pages 664-675.
• Eugene Hecht, Optics fourth edition, pages 460-464.

Credits:

The Multiple Slit Diffraction model was created by Fu-Kwun Hwang using the Easy Java Simulations (EJS) modeling tool. It was adapted to EJS version 4.1 by Robert Mohr and Wolfgang Christian at Davidson College. You can examine and modify the model for this simulation if you have EJS installed by right-clicking within the diffraction frame and selecting "Open Ejs Model" from the pop-up menu. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang,Robert Mohr, Wolfgang Christian; lookang; Félix J. García Clemente; Francisco Esquembre

http://iwant2study.org/lookangejss/04waves_11superposition/ejss_model_MultipleSlitDiffractionwee06/MultipleSlitDiffractionwee06_Simulation.xhtml

 

Briefing Doc: Multiple Slit Diffraction

Sources: Excerpts from "Young Double Slit or Single Slit or Multiple Slit Diffraction JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore"

Main Themes:

• Diffraction: This phenomenon describes how waves, including light, spread out as they pass through narrow openings or around obstacles.
• Interference: The way multiple waves interact with each other, leading to patterns of reinforcement (bright spots) and cancellation (dark spots).
• Single, Double, and Multiple Slit Diffraction: Exploring how the diffraction pattern changes depending on the number of slits involved.

Most Important Ideas/Facts:

1. Single Slit Diffraction:

• Produces a central bright fringe with diminishing fringes on both sides.
• The location of minima (dark spots) is determined by the equation: sin(θ) = mλ/D, where D is the slit width, λ is the wavelength, and m is an integer representing the order of the minimum.

1. Double Slit Diffraction:

• Famous for demonstrating the wave nature of light (Young's experiment).
• Creates an interference pattern of alternating bright and dark fringes.
• Bright fringes occur where waves from the two slits constructively interfere (in phase).
• Dark fringes occur where waves destructively interfere (out of phase).
• The location of bright spots is given by: d * sin(θ) = mλ, where d is the distance between slits.
• The location of dark spots is given by: d * sin(θ) = (m + 1/2)λ

1. Multiple Slit Diffraction (Gratings):

• Using more than two slits results in sharper and more defined interference patterns.
• The central maximum remains prominent, while side fringes become narrower and more intense.
• This is the principle behind diffraction gratings, used in applications like spectroscopy.

1. Interactive Simulation:

• The "Young’s Slit Diffraction Simulation Model" allows users to explore these concepts in an interactive way.
• Users can adjust parameters like wavelength, slit width, slit separation, number of slits, and screen distance to see how these changes affect the resulting diffraction pattern.

Quotes:

• "Multiple slits will sharpen (narrow) the regions of constructive interference. The overall pattern from multiple slits will be the two-slit pattern multiplied by the single slit diffraction envelope."This quote highlights how the complexity of the diffraction pattern increases with the number of slits.
• "This HTML5 applet is an invaluable educational tool for teachers, students, and enthusiasts alike. With real-time visualization, students can instantly see how their adjustments impact the diffraction pattern."This emphasizes the educational value of interactive simulations in making abstract physics concepts more accessible.

Conclusion:

Understanding the principles of diffraction and interference is crucial in many areas of physics and technology. The resources and interactive simulation discussed provide an excellent platform for exploring these concepts in detail, from basic single-slit scenarios to the more complex behavior of diffraction gratings.

 

Multiple Slit Diffraction Study Guide

Short Answer Questions

1. What is Fraunhofer diffraction?
2. Describe the diffraction pattern produced by a single slit.
3. What determines the location of minima in a single slit diffraction pattern?
4. How does the diffraction pattern change when you move from a single slit to a double slit setup?
5. What equation governs the location of bright spots in a double slit interference pattern?
6. Explain the difference between constructive and destructive interference.
7. How does the number of slits affect the interference pattern?
8. What is a diffraction grating?
9. How does changing the wavelength of incident light affect the diffraction pattern?
10. Give an example of a practical application of diffraction gratings.

Short Answer Key

1. Fraunhofer diffraction is a type of diffraction that occurs when light waves are incident on an obstacle and the resulting diffraction pattern is observed at a distance far from the obstacle, where the wavefronts can be considered planar.
2. A single slit produces a diffraction pattern characterized by a central bright fringe, which is the most intense, and alternating dark and bright fringes of decreasing intensity on either side of the central fringe.
3. The location of minima in a single slit diffraction pattern is determined by the equation: D sin(θ) = mλ, where D is the slit width, θ is the angle of diffraction, m is the order of the minimum, and λ is the wavelength of the light.
4. Moving from a single slit to a double slit setup introduces interference effects. The diffraction pattern now shows a series of equally spaced bright and dark fringes, resulting from the interference of light waves passing through the two slits.
5. The location of bright spots (constructive interference) in a double-slit interference pattern is governed by the equation: d sin(θ) = mλ, where d is the distance between the slits, θ is the angle of diffraction, m is the order of the bright spot, and λ is the wavelength of the light.
6. Constructive interference occurs when two waves meet in phase, resulting in a wave with a larger amplitude. Destructive interference happens when two waves meet out of phase, leading to cancellation or a wave with a reduced amplitude.
7. Increasing the number of slits in the setup sharpens and narrows the bright fringes in the interference pattern, making them more defined. The overall pattern is the result of the two-slit pattern modified by the single slit diffraction envelope.
8. A diffraction grating is an optical component consisting of a large number of equally spaced, parallel slits. It produces very sharp and bright interference patterns.
9. Changing the wavelength of the incident light affects the spacing of the fringes in the diffraction pattern. Longer wavelengths produce wider fringe spacing, while shorter wavelengths result in narrower fringe spacing.
10. Spectrometers are a practical application of diffraction gratings. They utilize the diffraction of light to separate and analyze different wavelengths present in a light source, helping determine the composition of materials.

Essay Questions

1. Explain in detail the phenomenon of diffraction. Discuss how the wave nature of light leads to diffraction, and describe the differences between Fraunhofer and Fresnel diffraction.
2. Compare and contrast the diffraction patterns produced by a single slit, double slit, and multiple slits. Discuss how the number of slits affects the interference pattern and the sharpness of the fringes.
3. Explain the concept of interference in the context of light waves. Describe constructive and destructive interference, and how they contribute to the formation of bright and dark fringes in diffraction patterns.
4. Discuss the mathematical relationships that govern the location of minima in single slit diffraction and the location of bright spots in double slit interference. Derive these equations and explain the significance of each variable.
5. Describe diffraction gratings and their applications. Explain how the properties of diffraction gratings make them useful in various scientific and technological fields.

Glossary of Key Terms

Diffraction: The bending or spreading of waves as they pass through an aperture or around an obstacle.

Fraunhofer Diffraction: A type of diffraction observed at a distance far from the obstacle, where wavefronts can be considered planar.

Fresnel Diffraction: A type of diffraction observed near the obstacle, where wavefronts are not planar.

Interference: The phenomenon that occurs when two or more waves interact, resulting in either reinforcement (constructive interference) or cancellation (destructive interference).

Constructive Interference: When two waves meet in phase, their amplitudes add up, resulting in a wave with a larger amplitude.

Destructive Interference: When two waves meet out of phase, their amplitudes cancel out, leading to a wave with a reduced amplitude or no wave at all.

Slit Width: The distance between the edges of a slit.

Slit Separation: The distance between the centers of two adjacent slits.

Wavelength (λ): The distance between two consecutive crests or troughs of a wave.

Order (m): An integer that represents the number of wavelengths that fit into the path difference between two interfering waves.

Diffraction Grating: An optical component consisting of a large number of equally spaced, parallel slits, used to produce sharp and bright interference patterns.

Spectrometer: An instrument that utilizes diffraction gratings to separate and analyze different wavelengths of light, commonly used to study the composition of materials.

Sample Learning Goals

[text]

For Teachers

Young’s Slit Diffraction: Exploring Single, Double, and Multiple Slits with JavaScript HTML5 Applet

Diffraction and interference of light have fascinated physicists for centuries, ever since Thomas Young’s famous double-slit experiment demonstrated the wave nature of light. Today, you can experience the power of this phenomenon in a modern, interactive way through the Young’s Slit Diffraction Simulation Model, a versatile JavaScript-based HTML5 applet. This applet allows users to experiment with single, double, and even multiple slits, offering a deeper understanding of how light waves interfere and create diffraction patterns.

Explore the simulation here: Young’s Slit Diffraction Simulation Model

Single, Double, and Multiple Slit Diffraction Explained

• Single Slit Diffraction: In the case of a single slit, light passing through the slit diffracts, spreading out as it moves toward the observation screen. The resulting pattern shows a central bright fringe (the most intense) flanked by diminishing fringes on both sides.

• Double Slit Diffraction: In Young’s famous experiment, two slits create an interference pattern of alternating bright and dark fringes. The bright fringes appear where the light waves from the two slits constructively interfere (waves meet in phase), while dark fringes occur where the waves destructively interfere (waves meet out of phase).

• Multiple Slit Diffraction (Gratings): When more than two slits are used, the interference pattern becomes sharper and more defined. The central maximum remains prominent, but the side fringes become narrower and more distinct. As the number of slits increases, the intensity of these fringes also increases.

Interactive Power: Vary the Number of Slits

The Young’s Slit Diffraction Simulation Model now offers a powerful new feature: the ability to vary the number of slits. This functionality lets users go beyond just double-slit experiments, allowing them to simulate diffraction with any number of slits. By adjusting the number of slits (N) using a simple slider, users can visually see the profound impact this has on the diffraction pattern.

For example:

• N = 1 simulates a single-slit experiment, showing a wide central maximum with diminishing side fringes.
• N = 2 replicates Young’s classic double-slit interference pattern.
• N = 12 demonstrates a diffraction grating, where multiple slits produce sharp, well-defined maxima and minima.

This flexibility makes the applet a versatile educational tool for demonstrating how interference patterns evolve with changes in slit configuration.

Key Adjustable Parameters

This applet gives users control over several key parameters that affect the diffraction pattern:

• Wavelength (λ): Adjusting the wavelength of light shows how the spacing of the interference fringes changes with different colors of light.
• Slit Width (a): Changing the width of the slits allows users to explore how the diffraction envelope (the outer shape of the fringes) is modulated.
• Slit Separation (d): This affects the spacing of the interference fringes. Larger slit separations result in narrower spacing between the fringes, while smaller separations spread them out.
• Number of Slits (N): As discussed, this is the new, powerful feature that lets users experiment with multiple slits to visualize diffraction gratings.
• Screen Distance (L): This controls how far the observation screen is from the slits, affecting the spread of the interference pattern on the screen.

By combining these adjustable features, users can recreate experiments ranging from single-slit diffraction to highly complex diffraction gratings, all within a single simulation.

Educational Value and Real-Time Visualization

This HTML5 applet is an invaluable educational tool for teachers, students, and enthusiasts alike. With real-time visualization, students can instantly see how their adjustments impact the diffraction pattern. This hands-on approach enhances the learning experience, making abstract concepts more tangible and engaging.

The simulation offers a way to explore:

• Wave-particle duality of light: Demonstrating that light exhibits both wave-like and particle-like properties.
• Constructive and destructive interference: Visualizing how waves interact to form bright and dark fringes.
• Diffraction grating applications: Understanding how multiple slits can be used in practical applications like spectrometers.

How to Use the Applet for Classroom Demonstrations

Educators can use this applet to make lessons on wave optics and diffraction more interactive:

• Start with a single slit to show how light spreads out due to diffraction.
• Increase to two slits and discuss Young’s double-slit experiment and its historical significance in proving the wave nature of light.
• Gradually increase the number of slits to show how diffraction gratings work in real-world applications like spectroscopy.
• Adjust the wavelength slider to explore how different colors of light (from red to violet) affect the diffraction pattern, linking this to the electromagnetic spectrum.

By engaging students with these interactive features, you can foster a deeper understanding of wave optics and interference phenomena.

Conclusion

The Young’s Slit Diffraction Simulation Model brings the beauty of wave interference to life in an accessible, interactive way. With the added ability to vary the number of slits, users now have more control than ever to experiment with and visualize the fascinating patterns that emerge when light passes through slits.

Whether you're a physics teacher demonstrating diffraction to a class, a student preparing for an exam, or just curious about wave phenomena, this applet is a fantastic resource for exploring the principles of diffraction and interference.

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2021/08/young-double-slit-or-single-slit-or.html
2. https://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2804.msg10149#msg10149 
3. https://www.compadre.org/osp/items/detail.cfm?ID=8331 
4. https://vle.learning.moe.edu.sg/moe-library/lesson/view/f7499ca4-6254-4429-83f5-fd1aafd35ea8/cover
5. https://weelookang.blogspot.com/2024/10/youngs-slit-diffraction-exploring.html

Other Resources

[text]

FAQ: Young's Slit Diffraction

1. What is diffraction?

Diffraction is the bending of waves as they pass through an aperture or around an obstacle. This phenomenon occurs with all types of waves, including light, sound, and water waves.

2. What is Young's Double Slit experiment?

Young's Double Slit experiment is a classic experiment demonstrating the wave nature of light. It involves shining a monochromatic light source through two narrow slits separated by a small distance. The light passing through the slits interferes with each other, creating a pattern of alternating bright and dark fringes on a screen placed behind the slits.

3. How does single-slit diffraction differ from double-slit diffraction?

Single-slit diffraction produces a pattern with a wide central bright fringe and progressively dimmer fringes on either side. Double-slit diffraction, however, produces a pattern of equally spaced bright and dark fringes due to the interference of light waves from both slits.

4. What happens when you increase the number of slits?

Increasing the number of slits creates a diffraction grating. This results in a sharper and more defined interference pattern. The central maximum remains prominent, but the side fringes become narrower, more distinct, and brighter.

5. What factors affect the diffraction pattern?

Several factors influence the diffraction pattern, including:

• Wavelength (λ): Shorter wavelengths create narrower fringe spacing, while longer wavelengths result in wider spacing.
• Slit width (a): A narrower slit width leads to a wider diffraction envelope (the overall shape of the fringes).
• Slit separation (d): Larger slit separations cause narrower spacing between the fringes, while smaller separations spread them out.
• Screen distance (L): A greater distance between the slits and the screen results in a more spread-out interference pattern.

6. What are the applications of diffraction gratings?

Diffraction gratings have various practical applications, including:

• Spectroscopy: Separating and analyzing different wavelengths of light to study the composition of materials.
• Telecommunications: Wavelength division multiplexing (WDM) in fiber optic systems for transmitting multiple signals over a single fiber.
• Optical instruments: Creating precision measurements and manipulating light in devices like lasers and monochromators.

7. What are some key learning goals associated with Young's Slit Diffraction?

• Understanding the wave-particle duality of light.
• Visualizing constructive and destructive interference.
• Comprehending the principles behind diffraction gratings and their applications.

8. What are some resources for further exploration of this topic?

• Young's Slit Diffraction Simulation Model: This interactive applet allows you to manipulate variables and observe their effects on the diffraction pattern.
• Textbooks: Physics textbooks often have detailed chapters on wave optics and diffraction.
• Online resources: Many websites and videos offer explanations and demonstrations of diffraction phenomena.