About

1.2.7 Example

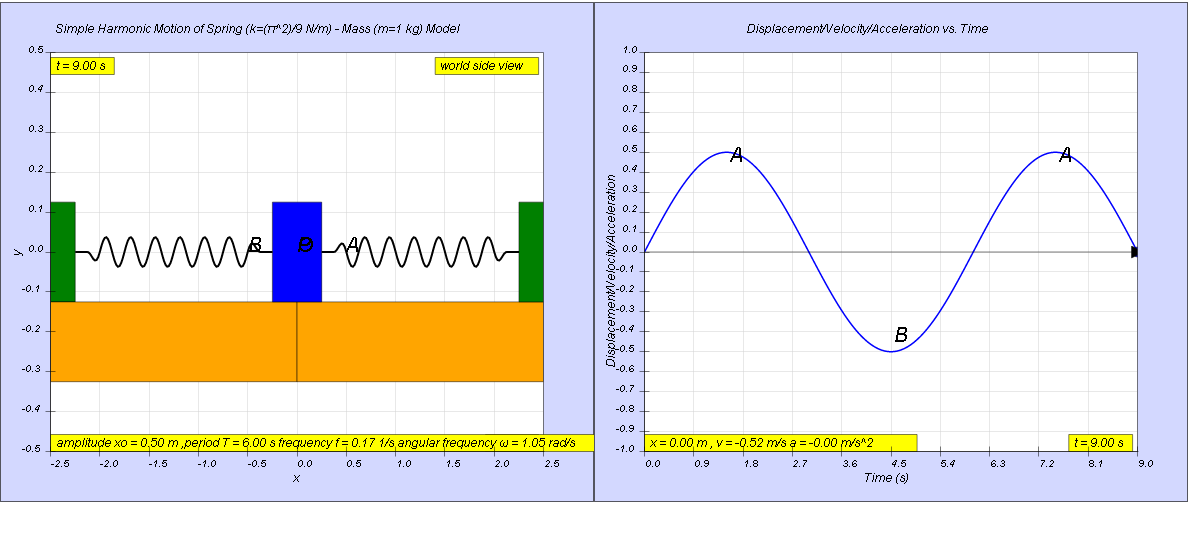
A body moves in a simple harmonic motion and the following graph gives the variation of its displacement x with time t.
 


a)    Write an equation to represent the given simple harmonic motion.
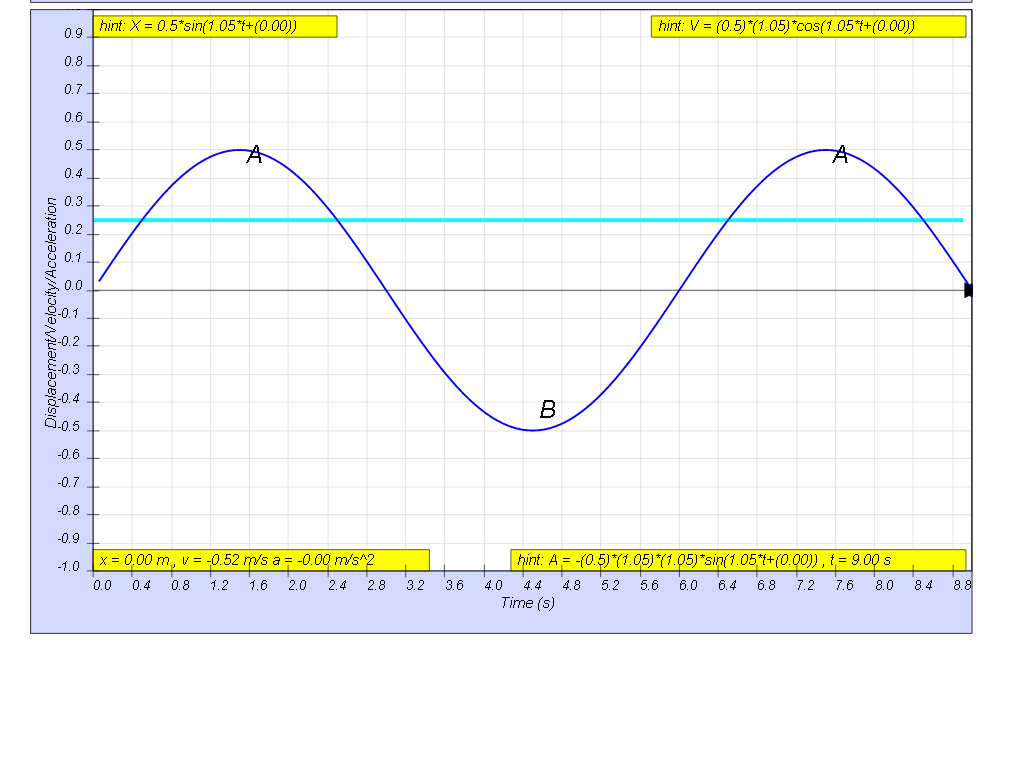
b)    Find the time duration in the first cycle when the body is located above a displacement of 0.25 m.

[ x = x_o sin (1.05 t) , Δt = 1.9 s ]

The hint can be found in the model

1.2.7.1 Solution:

a) x0 = 0.5 m

$\mathrm{since\; \omega }=\genfrac{}{}{0.1ex}{}{2\pi }{T}$ $\mathrm{,\; \omega }=\genfrac{}{}{0.1ex}{}{2\pi }{6.0}$$\mathrm{}$

ω = 1.05
x = x0sin(ω t) = 0.5 sin(1.05t)

b) At x = 0.25 m,

substituting back into the equation,

0.25 = 0.5 sin(1.05t)

$\mathrm{}$solving for t gives

0.5 = sin(1.05t)

$$
solving of the ranging of time, t

1.05t = 0.524 and π - 0.524

t₁ = 0.5 , t₂ = 2.4 s

looking at the graphical form of the solution of the 2 times, t₁ and t₂.

giving the range to be t₂ - t₁ = 2.4 - 1.5 = 1.9 s

1.2.7.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/76

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM13/SHM13_Simulation.xhtml

 

Briefing Document: ⚛️ Analysis of "10.2.7 Example Spring k=(π^2)/9 N/m, mass m=1 kg model versus Time for t = 1.5 Period JavaScript HTML5 Applet Simulation Model"

1. Overview:

This document analyzes a specific example of a simple harmonic motion (SHM) simulation model developed using Easy JavaScript Simulation (EJS). The model focuses on a spring-mass system with defined parameters (spring constant k and mass m) and aims to demonstrate the relationship between displacement (x) and time (t) in SHM. It’s designed as an interactive resource for educational purposes, accessible via web browsers and mobile devices.

2. Key Themes and Concepts:

• Simple Harmonic Motion (SHM): The primary focus is on SHM, a type of periodic motion where the restoring force is proportional to the displacement from equilibrium. The provided example models the motion of a mass attached to a spring.
• Mathematical Representation of SHM: The document emphasizes the importance of understanding the mathematical equations governing SHM. It presents the equation x = x0 sin(ωt) where:
• x is displacement at time t.
• x0 is the amplitude (maximum displacement).
• ω is the angular frequency.
• t is the time.
• Angular Frequency (ω): The document highlights the relationship between angular frequency (ω) and the period (T) of the motion, stated as ω = 2π / T. In this particular example, with a period T of 6.0, the angular frequency is calculated as ω = 2π / 6.0 ≈ 1.05.
• Solving for Time Intervals: A key educational goal is demonstrating how to use the SHM equation to solve for time intervals when the body is at a certain displacement. The document provides a specific example, stating how to calculate the time duration when the body is located above a displacement of 0.25m, by:
• Substituting x = 0.25m in the main equation.
• Solving for sin(1.05t), which then gives two different values of t (t1 = 0.5s and t2= 2.4s)
• Calculating the time range as t2-t1 = 1.9s
• Interactive Simulation: The model is not just theoretical; it is designed as a runnable simulation, allowing users to visualize and explore SHM dynamics. The embed code <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM13/SHM13_Simulation.xhtml " frameborder="0"></iframe> allows users to integrate the simulation directly into a webpage.

3. Important Ideas and Facts:

• Specific Example: The example used is a spring-mass system where the spring constant k = (π^2)/9 N/m and the mass m = 1 kg. These defined values allow for clear and specific mathematical solutions, and likely relate to the simulation model parameters.
• Amplitude Determination: The amplitude of the motion ( x0) is determined to be 0.5 m from the provided graph (although the graph is not directly available).
• Numerical Solutions: The document demonstrates a method to find specific time ranges by using the SHM equation and then referring to a graphical representation. It emphasizes that the analytical and graphical solutions match.
• Educational Context: The content is targeted towards a Junior College level, indicating an intended audience of higher secondary or early undergraduate students.
• Open Educational Resource: The material is hosted on an open educational resource platform, implying that it is intended for free use and sharing.
• Technology Integration: It showcases the use of JavaScript and HTML5 for creating interactive physics simulations that can be used across different platforms. It is accessible on "Android/iOS including handphones/Tablets/iPads" and "Windows/MacOSX/Linux including Laptops/Desktops" and "ChromeBook Laptops".

4. Key Quotes and Their Significance:

• "A body moves in a simple harmonic motion and the following graph gives the variation of its displacement x with time t.": This sentence immediately defines the context of the document as focusing on SHM and linking it to a displacement-time graph, showcasing the importance of visualising and interpreting these graphs.
• "x = x0 sin(ω t) = 0.5 sin(1.05t)": This equation is central to understanding the mathematical modeling of SHM, and shows a practical example of the equation in action.
• "looking at the graphical form of the solution of the 2 times, t1 and t2. giving the range to be t2 - t1 = 2.4 - 1.5 = 1.9 s": This highlights how the model helps visualize and calculate intervals, demonstrating that solutions need to be considered graphically to accurately find the requested range.
• "The hint can be found in the model": This statement encourages students to interact directly with the simulation to better understand the underlying concepts, suggesting that the interactive model is an important part of the learning process.

5. Connections to Other Resources:

The page also includes an extensive list of links to other related simulations and educational resources, covering topics such as:

• Other SHM models with different parameters.
• Gravitational fields and potential
• Projectile motion.
• Energy concepts.
• Optical physics phenomena (diffraction, resolution).
• Interactive math and science games.
• A wide range of educational tools and simulations, highlighting the breadth of the open source physics project.

6. Conclusion:

This document represents a specific instance of how interactive simulations can be used to teach core physics concepts. By combining a clear mathematical approach with an accessible and interactive visual model, the resource is able to demonstrate a strong pedagogical approach to teaching SHM. The numerous additional links highlight that the resource is part of a broader project that aims to provide a wealth of tools for physics education.

Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the maximum displacement of the oscillating body in the provided example?
2. What is the angular frequency (ω) of the simple harmonic motion in the example?
3. Explain the significance of the equation x = x₀sin(ωt) in the context of simple harmonic motion.
4. In the given problem, what physical quantity does ‘t’ represent, and what unit is it measured in?
5. What mathematical operation is used to find the time range when the body is above a certain displacement?
6. How is the value of 1.05 determined in the calculation of angular frequency?
7. What does the simulation model provided by the link allow users to do in this context?
8. What is the connection between the provided model and the problem presented in the text?
9. Explain the meaning of x₀ in the given equation.
10. Briefly describe the relationship between simple harmonic motion and the motion of a spring.

Answer Key

1. The maximum displacement (x₀) is 0.5 m. This represents the furthest point the oscillating body moves from its equilibrium position.
2. The angular frequency (ω) of the motion is 1.05 rad/s. This value dictates the rate at which the object oscillates.
3. The equation x = x₀sin(ωt) describes the displacement (x) of an object undergoing simple harmonic motion at any given time (t). It shows how the position varies sinusoidally over time.
4. 't' represents time, measured in seconds. It determines the point in the oscillation cycle we are observing.
5. The time range is found by subtracting two time values. These two times correspond to the moments when the body reaches the specified displacement, yielding a period duration.
6. The value 1.05 is calculated from ω = 2π / T. Here, T = 6.0 seconds, and it's calculated as 2π/6, which equals approximately 1.05 rad/s.
7. The simulation model allows users to visualize and interact with a simple harmonic motion, adjusting parameters to observe changes in the oscillation over time.
8. The model offers a visual, interactive way to demonstrate and better understand the solution to the problem presented which is an example of SHM.
9. x₀ represents the amplitude of the oscillation, which is the maximum displacement of the object from its equilibrium position.
10. Simple harmonic motion is often demonstrated by a mass attached to a spring, where the spring's restoring force causes the mass to oscillate back and forth with a characteristic pattern.

Essay Questions

Instructions: Answer the following essay questions, using evidence from the provided source to support your claims.

1. Discuss how the provided simulation model could be used to enhance a student's understanding of simple harmonic motion.
2. Analyze the mathematical solution to part b of the provided example, explaining each step and the physical meaning behind it.
3. Compare and contrast the relationship between the angular frequency, period, and time in the context of the example given.
4. Explain how the example problem and its solution might be used to illustrate a real-world application of simple harmonic motion.
5. Explain why it's important to use a model in conjunction with mathematical equations to understand simple harmonic motion.

Glossary of Key Terms

• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction.
• Displacement (x): The distance of an object from its equilibrium position. In SHM, it varies sinusoidally with time.
• Maximum Displacement (x₀): The greatest distance an object in SHM moves from its equilibrium position, also known as amplitude.
• Angular Frequency (ω): A measure of the rate of oscillation, measured in radians per second (rad/s). It is related to the period (T) by the formula ω = 2π/T.
• Time (t): A measure of the duration of an event or the point in time in a cycle. In the case of SHM, time helps track an object's position as it oscillates.
• Period (T): The time it takes for one complete cycle of oscillation.
• Amplitude: The maximum displacement from the equilibrium point.
• Sinusoidal: A curve that represents the sine function, characterized by its smooth, repetitive oscillation.
• Equilibrium Position: The rest position of an object, where no net force is acting upon it.
• Restoring Force: The force that acts to bring an object back to its equilibrium position when displaced.

 Video

https://notebooklm.google.com/notebook/d3a2f756-c0e3-4741-bf1a-bd4d5dd1d656/audio

Frequently Asked Questions

1. What is Simple Harmonic Motion (SHM) and how is it represented in the provided example? Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. In the example provided, a mass attached to a spring exhibits SHM. The motion is described mathematically by an equation of the form x = x₀ sin(ωt), where 'x' is the displacement at time 't', 'x₀' is the amplitude (maximum displacement), and 'ω' is the angular frequency. In the given example x = 0.5 sin(1.05t), indicating an amplitude of 0.5 meters and an angular frequency of 1.05 rad/s.
2. How can I determine the angular frequency (ω) from the period (T) of SHM? The angular frequency (ω) and the period (T) are related by the equation ω = 2π/T. In the provided example, the period (T) is approximately 6 seconds, which leads to an angular frequency (ω) of approximately 2π/6 ≈ 1.05 rad/s. This is used to construct the equation of motion in question 1.
3. How do I use the given SHM equation (x = 0.5 sin(1.05t)) to find the time when the body is at a specific displacement, like 0.25m? To find the time at which the body's displacement is 0.25m, you substitute x = 0.25m into the equation: 0.25 = 0.5 sin(1.05t). This simplifies to 0.5 = sin(1.05t). Solving for 't' requires taking the inverse sine (arcsin) of 0.5, which gives two solutions within one period of the sine function. These solutions represent the first time the body passes 0.25m going up and the second time the body passes 0.25m going down.
4. The solution calculates two times t1 and t2 for x=0.25m; how do we interpret the difference between t1 and t2? The two solutions t1 and t2 arise from the nature of the sine function, where each value within its range (between -1 and 1) is obtained twice within a single period. The smaller value (t1 = 0.5s) corresponds to the first time the mass reaches x = 0.25m while moving in one direction (usually considered positive displacement from zero equilibrium position), and the larger value (t2 = 2.4s) corresponds to the second time it reaches x = 0.25m when it's moving back in the opposite direction, having reached its maximum displacement and coming back to the equilibrium position. The time duration during which the body is at a displacement above 0.25m is calculated by t2 - t1 = 1.9s.
5. What is the purpose of the JavaScript HTML5 applet simulations referenced in the provided material? The JavaScript HTML5 applet simulations are interactive models designed for educational purposes. They visually demonstrate concepts in physics and math by simulating real-world scenarios. In the provided example, the simulation allows users to observe the motion of a mass-spring system exhibiting SHM, and it supports the mathematical equations by providing visual context. These simulations are accessible on various devices, including desktops, laptops, tablets and smartphones.
6. Besides SHM, what other physics concepts are explored through similar interactive simulations on this site? The website provides a variety of interactive simulations covering a broad range of physics topics. Besides SHM, these include oscillations, mechanics, collisions, electromagnetism, optics, thermodynamics, and many more. There are also simulations that tackle mathematics concepts like vectors, geometry, and calculus, and also topics in chemistry and geography, highlighting the diversity of the resources provided. There are also simulations relating to the use of physics concepts for building other devices, such as the 555 timer circuit.
7. What features do the interactive simulations offer, and how do they enhance learning? The interactive simulations typically allow users to manipulate parameters and observe the resulting changes in the simulated system. This direct manipulation helps build a more intuitive understanding of the concepts. Some simulations also provide graphs and other visuals that allow for quantitative analysis of the physical process. These features greatly enhance learning by making abstract concepts more concrete, allowing active and experiential learning by the student. The simulations are also easily embeddable, making them accessible for inclusion into other online learning resources.
8. What is WebEJS, and what role does it play in this context? WebEJS (Web Easy JavaScript Simulation) is a tool or platform for creating the interactive simulations featured on the site. It enables educators and developers to build and deploy interactive learning resources using JavaScript and HTML5. It aims to simplify the creation of interactive simulations, allowing those with minimal programming experience to develop educational content. The numerous references to "WebEJS workshop" and associated projects highlight the tool's role as a focal point for resource development by educators, and as a tool to encourage teachers to build and adapt open educational resources for their classes.