Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM08springconstantfrictionforce/SHM08springconstantfrictionforce_Simulation.xhtml

Briefing Document: Harmonic Oscillator Virtual Lab Simulation

Date: October 26, 2023 Subject: Review of the Harmonic Oscillator Virtual Lab HTML5 Applet Simulation Model Source: Open Educational Resources / Open Source Physics @ Singapore

1. Overview:

This document reviews the "Harmonic Oscillator Virtual Lab HTML5 Applet Simulation Model," an interactive tool developed by Open Educational Resources / Open Source Physics @ Singapore. The simulation aims to provide a virtual environment for exploring the principles of harmonic oscillation, particularly focusing on a spring-mass system with the inclusion of friction. The simulation is built using HTML5 and JavaScript, making it accessible on various devices including desktops, laptops, and mobile devices (Android/iOS).

2. Key Themes and Concepts:

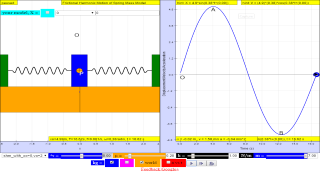
• Harmonic Oscillation: The simulation is designed to model the behavior of a mass attached to a spring, which undergoes harmonic motion. The core concept is that the spring exerts a restoring force proportional to the displacement from its equilibrium position, causing the mass to oscillate back and forth.
• Equilibrium Position: The simulation allows users to adjust the equilibrium position, which is "varied in this simulation." This is a key aspect as it changes the reference point for displacement and thereby the oscillation itself. "The spring will try to move back to its equilibrium position."
• Spring Constant (k): Although not explicitly mentioned as a variable to manipulate in the text, the formulas provided imply the simulation allows exploration of the effects of different spring constants.
• Friction: A significant feature of this simulation is the inclusion of a friction force between the block and the floor. The theory section states "here is a friction force between block and the floor, Fr= -mumg". This addition allows learners to explore damped harmonic motion, which is more realistic.
• Differential Equations: The simulation's underlying physics is governed by the following differential equations:
• dx/dt = v (velocity as the rate of change of position)
• dv/dt = a = (kx/m) - (μg/m) (acceleration determined by the spring force and frictional force)
• x is displacement from equilibrium
• v is velocity
• a is acceleration
• k is the spring constant
• m is mass
• μ is the coefficient of friction
• g is acceleration due to gravity
• Accessibility: The simulation's accessibility across different platforms is a deliberate choice to ensure a wider user base can engage with it. Its use of HTML5 ensures this can be achieved on modern devices.

3. Most Important Ideas and Facts:

• Simulation as a Learning Tool: The simulation serves as an interactive learning tool for understanding the concepts of harmonic oscillation, spring force, and friction. The interactive nature makes it ideal for students in junior college and beyond.
• Mathematical Representation: The explicit presentation of the differential equations allows the user to connect the underlying math with the observed behavior of the simulation. This bridges the gap between abstract theory and practical demonstration.
• Open Educational Resource: The simulation is part of a larger collection of open educational resources. This indicates an intention to promote accessible educational material. The materials are also shared under a Creative Commons license.
• Integration of Theory and Practical Observation: The simulation provides a real-time representation of the theoretical concepts being explored. This visual representation can aid in student understanding.
• Friction as Damping Force: The simulation models a critical aspect of real-world oscillatory systems - the damping effect introduced by friction. It shows how friction gradually decreases the amplitude of oscillations.
• Multi-Platform Compatibility: The fact that it works on desktops, laptops, and mobile devices highlights its emphasis on accessibility for varied student use.

4. Quotes from the Source:

• "The equilibrium position can be varied in this simulation."
• "The spring will try to move back to its equilibrium position."
• "here is a friction force between block and the floor, Fr= -mumg;"

5. Related Simulations and Resources: The provided source lists many other simulations on the site, suggesting that the Harmonic Oscillator applet is part of a large and comprehensive collection of interactive resources. Examples include: * Simulations for Kinematics and Projectile Motion. * Simulations related to Energy, Forces, Fields and Circular motion. * Simulations related to wave phenomena and optics. * Simulations related to atomic and nuclear physics. * Simulations that can be used as support for learning in other subjects, such as mathematics and chemistry.

6. Potential Use Cases:

• Classroom Demonstrations: Teachers can use the simulation as a visual aid during physics classes to explain harmonic motion and the effects of friction.
• Student Exploration: Students can use it as a virtual lab to conduct experiments and explore different parameters.
• Remote Learning: The online nature of the simulation makes it ideal for remote learning environments.
• Conceptual Understanding: The visual nature aids students in creating a more concrete mental image of the concepts.

7. Technical Details and Credits:

• The simulation was created using the Easy JavaScript Simulation (EJS) framework and is embedded using an iframe.
• Credits are given to the developers of EJS and links to relevant blogs are given.
• The resource is part of the Open Educational Resources / Open Source Physics @ Singapore project.
• The licensing information is also provided, allowing others to use and share the simulation under specific terms.

8. Conclusion:

The Harmonic Oscillator Virtual Lab simulation offers a valuable, interactive, and accessible learning tool for students studying the physics of oscillatory motion. Its inclusion of friction as a damping force, along with its multi-platform compatibility, makes it a strong educational resource for both classroom and individual study. The emphasis on open educational resources is also significant, making this resource widely available.

 

Harmonic Oscillator Simulation Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the primary function of the virtual lab simulation described in the text?
2. What is meant by the term "equilibrium position" in the context of the simulation?
3. According to the provided theory, what two forces affect the block’s acceleration?
4. What do the differential equations shown in the text represent?
5. What does the variable k represent in the differential equation provided?
6. What does the variable μ represent in the provided differential equation?
7. What platforms are compatible with the simulation, as stated in the document?
8. What is the nature of the friction force in the model and how is it calculated?
9. How does the simulation allow users to vary the equilibrium position of the system?
10. What is the general topic area of most of the resources linked at the bottom of the page?

Quiz Answer Key

1. The primary function of the virtual lab simulation is to model the behavior of a harmonic oscillator, allowing users to observe and understand how a spring system behaves with applied forces. The simulation allows variation in spring constant, friction, and initial conditions.
2. In this context, "equilibrium position" refers to the location where the spring exerts no net force on the block, representing the resting point of the system when no outside forces are acting other than the spring and gravity. The position can be varied in the simulation.
3. The two forces that affect the block’s acceleration are the spring force, which acts to restore the block to the equilibrium position, and the frictional force between the block and the floor.
4. The differential equations ( \frac{dx}{dt} = v ) and ( \frac{dv}{dt} = a = \frac{k x}{m} - \frac{\mu g }{m} ) describe the motion of the block where dx/dt is velocity, and dv/dt is the acceleration of the mass. The second equation also factors in the spring constant, mass, friction coefficient, and gravity.
5. The variable k represents the spring constant in the equation, which quantifies the stiffness of the spring; a higher value of k means a stiffer spring.
6. The variable μ represents the coefficient of friction in the equation, which quantifies the amount of friction between the block and the floor.
7. The simulation is compatible with a variety of platforms including Android, iOS devices, Windows, MacOSX, Linux, and Chromebooks.
8. The friction force is a force that opposes the motion of the block. It is calculated as Fr= -mumg, where mu is the coefficient of friction, m is the mass, and g is gravity.
9. The simulation allows users to vary the equilibrium position by adjusting a setting or input parameter within the simulation’s interface; however, the document does not describe how to do this.
10. Most of the resources linked at the bottom of the page focus on physics and mathematics modeling, often utilizing simulations and interactive tools to help visualize complex principles.

Essay Questions

Instructions: Answer each of the following questions in a well-organized essay format. You should include an introduction paragraph, a body with supporting information, and a conclusion.

1. Explain how the spring constant, k, affects the behavior of the harmonic oscillator and how this can be observed in the simulation.
2. Discuss the role of friction, represented by μ, in the harmonic oscillator model and how it affects the long-term motion of the system.
3. Describe the relationship between the differential equations provided in the simulation's theory and how they relate to the graphical output of the system's motion.
4. Compare and contrast the various platforms supported by the simulation and the benefits these platforms bring to different user groups.
5. Evaluate the educational value of this type of virtual lab simulation compared to traditional methods of learning about harmonic oscillators.

Glossary

Equilibrium Position: The point where the spring is at rest and exerts no net force on the block, or the resting position of the harmonic oscillator, which can be varied in the simulation.

Harmonic Oscillator: A system that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement. Examples include a mass on a spring or a pendulum.

Spring Constant (k): A measure of the stiffness of a spring; the higher the constant, the stiffer the spring and the more force required to stretch or compress it.

Coefficient of Friction (μ): A dimensionless scalar value that represents the ratio of the force of friction between two surfaces.

Differential Equations: Equations that describe the relationship between a function and its derivatives; used to model systems that change over time, including the movement of an oscillating object.

Virtual Lab: A simulated environment that allows users to perform experiments or explore concepts using a computer or other devices, often without needing physical equipment.

Frictional Force (Fr): A force that opposes the motion between two surfaces in contact. In the model it is calculated as Fr= -mumg where m is mass and g is gravity.

HTML5 Applet: An interactive program, written using web standard technologies (HTML5, CSS and JavaScript) that runs inside a web browser, often used to create educational simulations.

Kinematics: The study of motion without considering the causes of that motion.

Restoring Force: The force that acts to return a displaced system to its equilibrium position, like the force exerted by a spring or gravity on a pendulum.

 Theory

The equilibrium position can be varied in this simulation.  
The spring will try to move back to it's equilibrium position.

The differential equations are: 

\( \frac{dx}{dt} = v \)

\( \frac{dv}{dt} = a = \frac{k x}{m} - \frac{\mu g }{m} \)

here is a friction force between block and the floor, Fr= -mu*m*g;

Reference:

1. http://weelookang.blogspot.sg/2016/04/harmonic-oscillator-virtual-lab.html
2. http://weelookang.blogspot.sg/2015/01/shm-chapter-08.html
3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1084.0 Java Simulation by Fu-Kwun Hwang

 

FAQ: Harmonic Oscillator Simulation

• What is a harmonic oscillator, and how is it represented in this simulation?
• A harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement. This simulation models a mass attached to a spring, where the spring's force attempts to pull the mass back to its equilibrium point. The simulation allows you to change the equilibrium position. The restoring force and its impact on position and motion are the key focus.
• What are the main physical factors affecting the harmonic motion in this simulation?
• The main factors are the spring constant (k), which determines the strength of the restoring force; the mass (m), which influences the inertia of the system; and friction (represented by µg). The spring constant and mass are part of the equation ( \frac{dv}{dt} = a = \frac{k x}{m} ) and the friction is represented in the equation (- \frac{\mu g }{m} ). These factors directly determine the frequency, amplitude and damping of the oscillator's motion.
• How does friction impact the oscillations in this model?
• The simulation includes a frictional force between the mass and the surface it moves on. This force, denoted as Fr = - µmg, acts opposite to the direction of motion and dissipates energy. It causes the oscillations to gradually decrease in amplitude, eventually bringing the system to rest at the equilibrium position. The coefficient of friction (µ) determines the strength of this damping.
• What equations govern the motion of the mass in this simulation?
• The motion is governed by the following differential equations:
• ( \frac{dx}{dt} = v ), which relates the rate of change of position (x) to the velocity (v).
• ( \frac{dv}{dt} = a = \frac{k x}{m} - \frac{\mu g }{m} ), which relates the rate of change of velocity (v) (i.e. acceleration, a) to the restoring force of the spring ((\frac{k x}{m})) and the friction force ((\frac{\mu g }{m})).
• These equations mathematically define how the mass's position and velocity evolve over time.
• Can this simulation be used on various devices and operating systems?
• Yes, this simulation is developed using HTML5 and EasyJavaScriptSimulation and is designed to be compatible with a wide range of devices. It works on Android/iOS devices (including phones and tablets), Windows/MacOSX/Linux computers (including laptops and desktops), and Chromebook laptops, ensuring accessibility for various users.
• Are there other types of physics simulations available through this platform? Yes, there are a wide array of physics simulations available through this platform, including those that model kinematics, projectile motion, collisions, circular motion, energy, gravity, electromagnetism, wave phenomena, optics, quantum physics and much more. These simulations vary in topic, complexity, and focus to support the learning of many concepts in physics.
• Is there a community or way to learn more about creating these types of simulations? Yes, there is a community around the creation and use of these simulations. The platform includes information regarding workshops and lectures (specifically referencing Douglas Brown, Wolfgang Christian, Francisco Esquembre and Fu-Kwun Hwang), which suggest a dedicated community engaged in developing and teaching with these tools. Further, resources such as the Easy JavaScript/Java Simulation Authoring and Modeling Tool indicate that people can learn to create their own simulations.
• Is the material open source and available for use?
• Yes, the resources on this site are primarily open educational resources licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License. This means the educational content is available for others to use and adapt freely, as long as proper attribution is given and the modified works are shared under the same license. However, commercial use of the EasyJavaScriptSimulations library requires separate licensing and contact with the indicated email and url.