About

Topics

Description

Sample Learning Goals

Activities

Version:

1. http://weelookang.blogspot.sg/2013/12/sliding-block-and-spring-model-by.html

http://weelookang.blogspot.sg/2013/12/sliding-block-and-spring-model-by.html

Frictional, spring, and gravitational forces act on as block as it slides on an inclined plane.

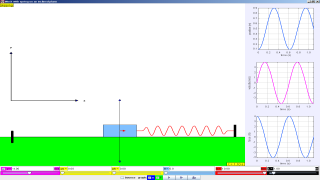
Block and Spring on an Inclined Plane

The Block and Spring on an Inclined Plane model displays the dynamics of a mass-spring system sliding on an inclined plane with static and kinetic friction.  The model shows the asymmetry caused by the change in direction of the frictional force when sliding up and down the incline and the importance of friction in establishing equilibrium.  When the block is sliding, Newton's law for motion for a mass m moving along the incline of length L can be written as

 

where k is the spring constant in N/m, μ_k is the kinetic (sliding) coefficient of friction, θ is the angle of the incline, and g is the acceleration of gravity in m/s^2.  We use the + sign when the block is moving to the right and - sign when the block is moving to the left.  Note that the model uses a unit mass block and a natural spring length of L/2 in order to limit the number of input parameters.

 

The static friction force prevents motion until some limit where motion occurs.  It is characterized by a static coefficient of friction  μ_s and is equal and opposite to the net applied force less than a maximum value

where the normal force N is that component of the gravitational force that presses the block into the plane.  The static coefficient of friction is harder to quantify than the kinetic coefficient but is generally larger than the kinetic coefficient and may arise from surface irregularities and surface contaminants.

 

The Block and Spring on an Inclined Plane model displays the numerical solution to this equation and shows how the forces change as the mass slides.  The scale of the force vectors is arbitrary and that the image is rescaled as the incline plane length is varied from 0.1 to 10 m or the incline angle is changed.  Users can set the coefficients of friction and the spring constant. The model plots the position, velocity, and net force on the mass as a function of time as the system evolves.

 

References:

• "Damped oscillations and equilibrium of a mass-spring system subjected to sliding friction forces: integrating experimental and theoretical analysis," P. Onorato, D. Mascoli, and A. DeAmbrosis, American Journal of Physics, (in press).

Credits:

The Block and Spring on an Inclined Plane model was created by Wolfgang Christian using the Easy Java Simulations (EJS) version 4.3 authoring and modeling tool. 

 

You can examine and modify a compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu.  You must, of course, have EJS installed on your computer.  Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

 

Translations

Code	Language		Translator	Run

Credits

Wolfgang Christian, remixed by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.) for simple harmonic motion; lookang

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_BlockAndSpringOnInclinedPlanewee/BlockAndSpringOnInclinedPlanewee_Simulation.xhtml

Briefing Doc: Block and Spring on an Inclined Plane

Source: "Block and Spring on an Inclined Plane JavaScript HTML5 Applet Simulation Model by Wolfgang Christian - Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore"

Main Themes:

• Dynamics of a mass-spring system on an inclined plane: This resource focuses on explaining the motion of a block attached to a spring while sliding on an inclined plane under the influence of gravity, friction (both static and kinetic), and the spring force.
• Impact of Friction: The document highlights the crucial role friction plays in the system's equilibrium and the differences between static and kinetic friction. It emphasizes the asymmetry caused by the changing direction of the frictional force as the block moves up and down the incline.
• Mathematical Modeling: The resource presents Newton's second law applied to the block's motion on the inclined plane. It details the equations governing the forces involved and discusses parameters like the spring constant, coefficients of friction, angle of incline, and acceleration due to gravity.
• Interactive Simulation: The resource describes an interactive JavaScript simulation model that visually demonstrates the concepts explained. It allows users to adjust parameters like friction coefficients and spring constant and observe the resulting changes in the block's motion, forces, position, velocity, and net force over time.

Most Important Ideas/Facts:

• Newton's law for the block's motion: "When the block is sliding, Newton's law for motion for a mass m moving along the incline of length L can be written as [equation]" This equation highlights the interplay of the spring force, gravitational force, and frictional force in determining the block's acceleration.
• Static Friction: "The static friction force prevents motion until some limit where motion occurs. It is characterized by a static coefficient of friction μs and is equal and opposite to the net applied force less than a maximum value [equation]." This explains how static friction acts as a threshold force that needs to be overcome for the block to start moving.
• Kinetic Friction: " μk is the kinetic (sliding) coefficient of friction" This introduces the concept of kinetic friction, which acts opposite to the direction of motion once the block starts sliding.
• Importance of the simulation: "The Block and Spring on an Inclined Plane model displays the numerical solution to this equation and shows how the forces change as the mass slides. The scale of the force vectors is arbitrary and that the image is rescaled as the incline plane length is varied from 0.1 to 10 m or the incline angle is changed." The simulation provides a visual and interactive way to understand the complex interplay of forces and their effect on the block's motion, making it easier to grasp the theoretical concepts.

Quotes:

• Equation of motion: "...Newton's law for motion for a mass m moving along the incline of length L can be written as [equation]"
• Static friction: "The static friction force prevents motion until some limit where motion occurs..."

Overall, this resource provides a comprehensive overview of the dynamics of a block-spring system on an inclined plane. It combines theoretical explanations, mathematical equations, and an interactive simulation to help users understand the interplay of forces and their effects on the system's motion.

 

Block and Spring on an Inclined Plane Study Guide

Glossary of Key Terms

TermDefinitionInclined PlaneA flat surface set at an angle, other than a right angle, to the horizontal.Spring Constant (k)A measure of a spring's stiffness, represented in N/m.Static Friction (μs)The force that opposes the initiation of motion between two surfaces in contact.Kinetic Friction (μk)The force that opposes the continued motion between two surfaces in contact.Normal Force (N)The force exerted by a surface that supports the weight of an object resting on it. This force acts perpendicular to the surface.Gravitational ForceThe force of attraction between any two objects with mass.EquilibriumA state where the forces acting on an object are balanced, resulting in no net acceleration.OscillationRepetitive back and forth motion around a central point or equilibrium position.AmplitudeThe maximum displacement from the equilibrium position during an oscillation.PeriodThe time taken for one complete cycle of oscillation.Short Answer Quiz

1. Explain how the angle of an inclined plane affects the forces acting on a block placed upon it.
2. Differentiate between static and kinetic friction. Which is generally greater?
3. Describe the role of the spring constant in the equation of motion for the block and spring system on an inclined plane.
4. What condition must be met for the block to begin moving up the incline?
5. How does the direction of the frictional force change when the block slides up and down the inclined plane?
6. Explain the concept of equilibrium in the context of the block and spring system.
7. What factors influence the period of oscillation for the block and spring system?
8. How would increasing the mass of the block affect the system's behavior?
9. Why is it important to consider friction when analyzing the motion of the block on the inclined plane?
10. Briefly describe how the "Block and Spring on an Inclined Plane" model contributes to understanding this physical system.

Short Answer Quiz Answer Key

1. The angle of the incline affects the components of the gravitational force acting on the block. A larger angle increases the component of gravity pulling the block down the incline and decreases the normal force.
2. Static friction is the force that prevents an object from moving initially, while kinetic friction acts once the object is in motion. Static friction is generally greater than kinetic friction.
3. The spring constant (k) represents the spring's stiffness. A larger spring constant means a stiffer spring that exerts a greater force for a given displacement. In the equation of motion, the spring force is proportional to the spring constant and the displacement from equilibrium.
4. For the block to move up the incline, the force provided by the spring must exceed the sum of the static friction force and the component of gravity acting down the incline.
5. The frictional force always acts opposite to the direction of motion. When the block slides up the incline, friction acts down the incline, and when the block slides down, friction acts up the incline.
6. Equilibrium in this system is reached when the net force on the block is zero. This can occur when the block is at rest or when the forces from the spring, gravity, and friction balance each other out, resulting in constant velocity motion.
7. The period of oscillation is primarily influenced by the mass of the block and the spring constant. A larger mass or smaller spring constant will lead to a longer period.
8. Increasing the block's mass would make the system more resistant to changes in motion. It would require a greater force to start and stop the block, and the period of oscillation would increase.
9. Friction plays a crucial role in dissipating energy in the system. Without friction, the block would oscillate indefinitely. Considering friction allows for a more realistic model that accounts for energy loss and the eventual damping of oscillations.
10. The model provides a visual representation of the system's dynamics, allowing users to manipulate variables and observe their effects on motion. It helps to visualize the forces at play, the resulting motion, and the interplay between factors like friction, gravity, and spring force.

Essay Questions

1. Derive the equation of motion for the block and spring system on an inclined plane, considering both static and kinetic friction. Explain each term in the equation and discuss its significance.
2. Analyze the energy transformations that occur as the block oscillates on the inclined plane. Discuss the roles of potential energy (gravitational and elastic), kinetic energy, and energy dissipation due to friction.
3. Compare and contrast the motion of the block and spring system on an inclined plane with the motion of a simple pendulum. Discuss the similarities and differences in their equations of motion, periods, and energy transformations.
4. Investigate the conditions under which the block and spring system on an inclined plane exhibits damped oscillations, underdamped oscillations, and overdamped oscillations. Explain how the values of the system parameters affect the type of oscillation.
5. Design an experiment to determine the coefficient of kinetic friction between the block and the inclined plane. Outline the procedure, the data you would collect, and the calculations necessary to arrive at the coefficient of friction.

Other Resources

1. https://www.geogebra.org/m/MQpSdK2A Inclined Plane with Two Masses and a Pulley by ukukuku

Block and Spring on an Inclined Plane FAQ

1. What is the purpose of the Block and Spring on an Inclined Plane model?

This model demonstrates the physics of a mass-spring system on an inclined plane, including the impact of static and kinetic friction. It visually illustrates the force changes as the mass moves and helps users understand the concept of equilibrium.

2. What physical principles are involved in this model?

The model is based on Newton's laws of motion, specifically the second law (F=ma), applied to motion on an incline. It incorporates the forces of gravity, spring force, static and kinetic friction, and the normal force.

3. How does friction affect the motion of the block?

Friction plays a crucial role in this system. Static friction prevents the block from moving until the applied force overcomes a certain threshold. Once the block starts moving, kinetic friction opposes the motion, leading to energy dissipation and eventual stopping of the block.

4. What are the key parameters that can be adjusted in the model?

The model allows users to modify the coefficients of friction (both static and kinetic) and the spring constant. These adjustments demonstrate how changing these parameters affects the block's motion and the forces acting on it.

5. What types of graphs are provided by the model?

The model generates graphs depicting the position, velocity, and net force acting on the block as a function of time. These visualizations help users understand the dynamic behavior of the system.

6. What is the significance of the asymmetry observed in the block's motion?

The asymmetry arises from the change in the direction of the frictional force when the block slides up and down the incline. Friction always acts opposite to the direction of motion, resulting in different force magnitudes and motion characteristics.

7. How does the model handle the varying scale of forces?

The model uses an arbitrary scale for the force vectors, and the image is automatically rescaled when the incline plane length or angle changes. This ensures clear visualization regardless of the parameter settings.

8. Where can I find more information or resources related to this model?

Additional details, including the underlying equations and references, are available in the "About" section of the model webpage. The site also provides links to related resources and the source code for further exploration.