Here are the document brief, study guide, and FAQ for the Tracker Modeling of Two Pendulums Swinging in Anti-Phase.

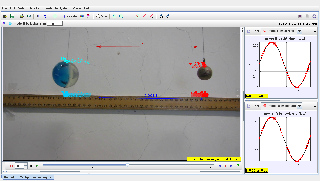
Document Brief: Modeling Two Pendulums Swinging in Anti-Phase Using Tracker

This document explores the motion of two pendulums swinging in anti-phase, using Tracker software for motion analysis and modeling. Anti-phase motion occurs when one pendulum reaches its maximum displacement in one direction while the other reaches its maximum displacement in the opposite direction. The motion is analyzed in Cartesian coordinates with position functions describing the synchronized but opposite oscillations.

Purpose:

To analyze and model the dynamics of two pendulums swinging in anti-phase, investigating their displacement, velocity, and synchronization using Tracker.

Key Features:

• Motion tracking of two pendulums with opposite oscillatory motion.
• Position functions describing anti-phase motion:
  • $x=A\sin (\omega t+\varphi )$ and $x=-A\sin (\omega t+\varphi )$.
• Graphical analysis of displacement ($x,y$) vs. time ($t$).

Study Guide: Modeling Two Pendulums in Anti-Phase

Learning Objectives:

1. Understand the concept of anti-phase motion in pendulums.
2. Analyze displacement vs. time graphs to validate the periodic motion in anti-phase.
3. Explore the relationship between theoretical position functions and experimental tracking data.

Step-by-Step Guide:

1. Setup and Calibration:

   • Import the video of the two pendulums swinging in anti-phase into Tracker.
   • Calibrate the scale using the ruler visible in the video.

2. Tracking Motion:

   • Track the position of both pendulums frame by frame.
   • Record displacement data along the $x$-axis for each pendulum.

3. Define Position Functions:

   • Open Tracker’s Model Builder.
   • For each pendulum, define the position functions:
     • For Pendulum 1: x1=Asin⁡(ωt+ϕ)x_1 = A \sin(\omega t + \phi)x1​=Asin(ωt+ϕ),
     • For Pendulum 2: x2=−Asin⁡(ωt+ϕ)x_2 = -A \sin(\omega t + \phi)x2​=−Asin(ωt+ϕ),
     • where:
       • $A$ is the amplitude,
       • $\omega$ is the angular frequency,
       • $\varphi$ is the phase offset.
     • $y=0$ (motion is along the horizontal axis).

4. Graphical Analysis:

   • Plot $x$-displacement vs. $t$:
     • Verify that the pendulums oscillate with the same frequency but in opposite directions.
     • Observe how their motions are synchronized but 180° out of phase.
   • Compare experimental data with theoretical position functions to validate the model.

5. Applications:

   • Study coupled oscillatory systems with opposite-phase synchronization.
   • Explore real-world scenarios such as balancing oscillatory systems or anti-phase synchronization in machinery.

Tips for Success:

• Ensure accurate tracking of both pendulums for reliable data and analysis.
• Cross-check the amplitude and angular frequency values between theoretical and experimental models.

FAQ: Modeling Two Pendulums Swinging in Anti-Phase

1. What does anti-phase motion mean?

In anti-phase motion, the two pendulums oscillate with the same frequency but in opposite directions. When one pendulum reaches its maximum displacement in one direction, the other reaches its maximum displacement in the opposite direction.

2. How are the position functions defined?

• Pendulum 1: x1=Asin⁡(ωt+ϕ)x_1 = A \sin(\omega t + \phi)x1​=Asin(ωt+ϕ),
• Pendulum 2: x2=−Asin⁡(ωt+ϕ)x_2 = -A \sin(\omega t + \phi)x2​=−Asin(ωt+ϕ), where $A$ is the amplitude, $\omega$ is the angular frequency, and $\varphi$ is the phase offset.

3. What do the displacement graphs show?

The displacement graphs show periodic motion, with the two pendulums oscillating in synchrony but 180° out of phase.

4. Why do the pendulums oscillate with opposite phases?

Anti-phase motion can result from initial conditions where one pendulum is displaced in one direction and the other in the opposite direction.

5. How can this analysis be applied?

• Understanding coupled oscillatory systems.
• Designing mechanical systems with anti-phase synchronization to reduce vibrations.
• Exploring natural systems, such as alternating movements in biological systems.

6. Can this model include damping or external forces?

Not directly. The current model assumes ideal conditions without damping. Damping or external forces can be added as additional terms in the equations.

7. What are the practical applications of this model?

• Studying oscillatory systems in engineering, such as engines or pendulum-based machines.
• Exploring synchronization and phase relationships in coupled systems.