About

7.3.8.6 Example of Application of potential ϕ

7.3.8.6.1 Revision:

  The total ϕ at a point in a field due to two or more source masses is the scalar addition of the individual ϕ due to each mass at that point, i.e.  .
ϕ_total = ∑ϕ

Similarly, since PE = U = mϕ

PE _total = $m\sum \varphi$

Showing how the gravitational potential varies between the surface of the Moon and the surface of the Earth along the line joining the centres.

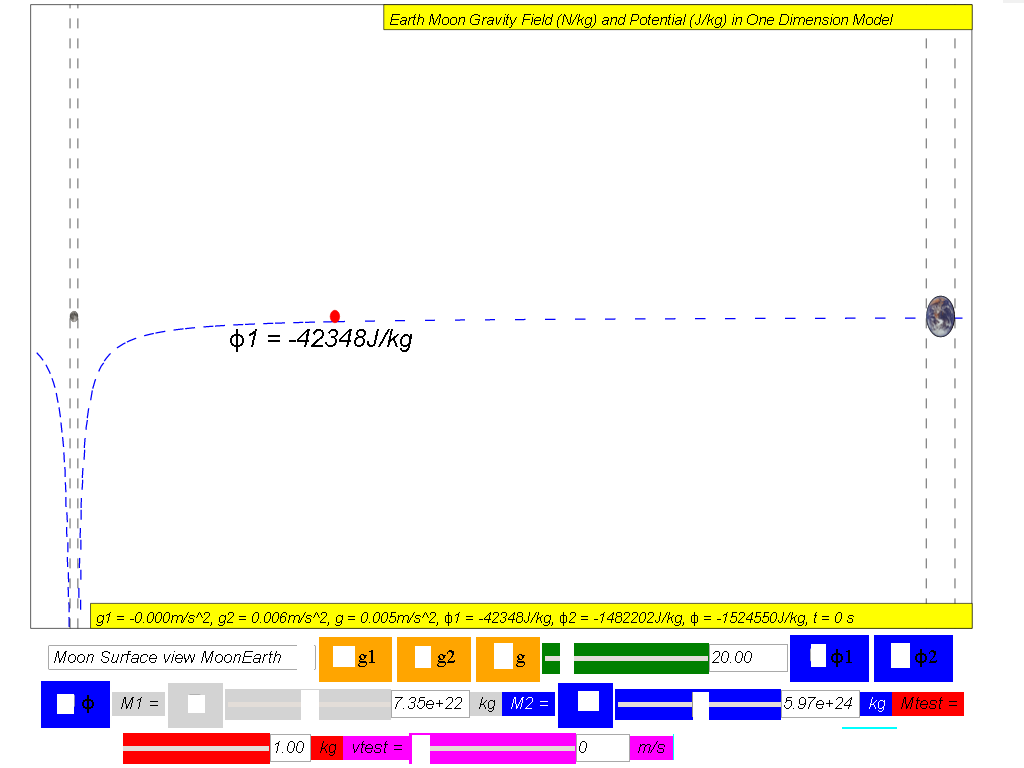
ϕ₁ = Gravitational potential due to Moon

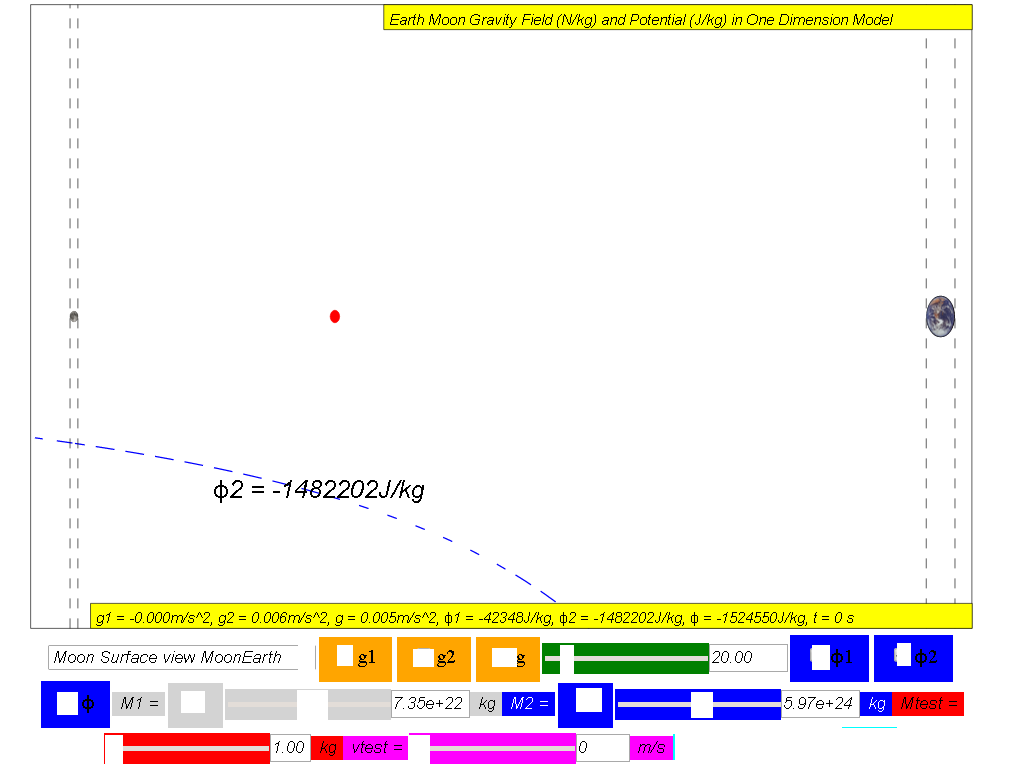ϕ₂ = Gravitational potential due to Earth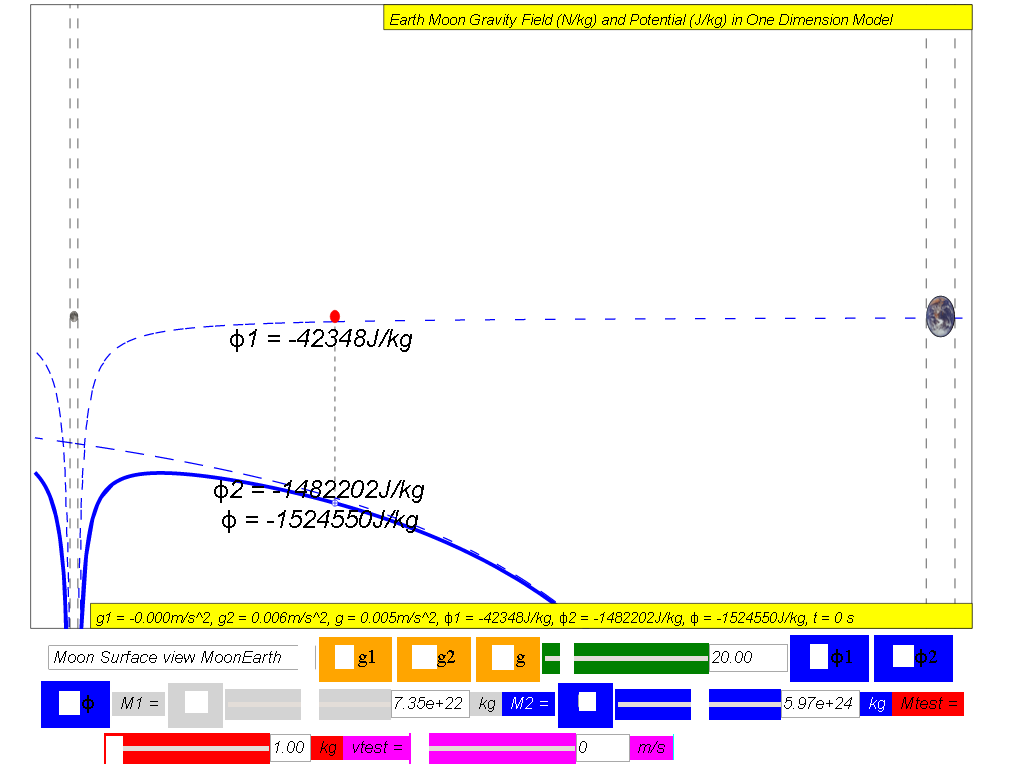



ϕ_total = ϕ₁ +ϕ₂ = Net gravitational potential along the line of centres is equal to the sum of the gravitational potentials due to the Earth and Moon

7.3.8.6.2 Escape Speed Is it true that 'what goes up must come down'? 

It is only accurate to say that 'what goes up may come down'.  There is a critical speed at which an object can be launched such that it can escape the Earth permanently.  Such a critical speed is termed as the escape speed.

7.3.8.6.2.1 Example Determine an expression for the escape speed, v, of a rocket of mass m launched from the surface of Earth of mass M and radius R.

By conservation of energy, assuming at r = ∞, the minimum speed is 0.

KE_{earth surface} + PE_{earth surface} = KE_∞ + PE_∞

$\genfrac{}{}{0.1ex}{}{1}{2}m{v}^2+\left(\genfrac{}{}{0.1ex}{}{-GmM}{r_{earth}}\right)=0+0$

$\genfrac{}{}{0.1ex}{}{1}{2}{v}^2+\left(\genfrac{}{}{0.1ex}{}{-\left(6.67x10^{-11}\right)\left(6.0x10^{24}\right)}{6.37x10^6}\right)=0+0$

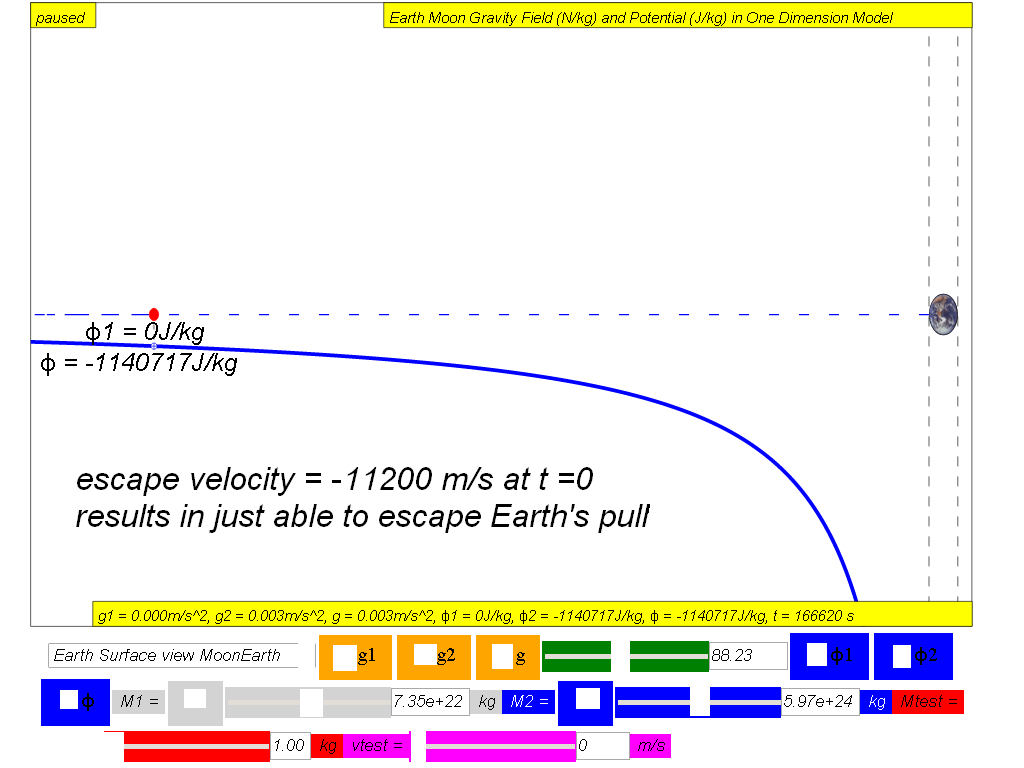
v = 1.12x10⁴ m/s

Therefore, to escape from Earth, it implies that the projectile must have a minimum launch velocity of v = 1.12x10⁴ m/s .





To understand the escape velocity concept, the following steps could be used as an inquiry approach to experience escape velocity in the context of the simulation.

1. Un-check the M1 moon to remove the effects of the Moon
2. Select from the drop-box menu the option Earth Surface view MoonEarth (Left to Right), and notice the test mass (red) is placed on the surface of the Earth on the right side.
3. Key in on the vtest, velocity of the test mass (magenta) say -10000 m/s (negative as the velocity points to the left of the Cartesian coordinate system)), and click play to observe the effects of launching a projectile at this speed. You could record your observation as "unable to escape from Earth's gravity pull.

Similarly, design an experiment to discover the minimum theoretical speed to escape from Earth's pull.

Can you conclude that any velocity lesser than v = 1.12x10⁴ m/s cannot allow the projectile to escape from Earth's pull?

Can you conclude that any velocity greater than v_{escape Earth} = 1.12x10⁴ m/s allow the projectile to escape from Earth's pull?


Similarly,  you can derive the theoretical escape velocity from Earth's Moon surface and test it on the simulation.
Answer: v_{escape Moon}=2400 m/s


Given that root-mean-square speed is the measure of the speed of particles in a gas that is most convenient for problem solving within the kinetic theory of gases,  is given by $v_{rms}=\sqrt{(}\genfrac{}{}{0.1ex}{}{3RT}{Mm})$

Given molar gas constant R = 8.31 J K⁻¹ mol⁻¹, molar mass of water is Mm H₂0 = 18x10^-3 kg/mol , T is temperature in Kelvin, using the minimum theoretical speed from Moon, suggest the surface temperature of Moon at some point in its history which resulted in the Moon's surface not having water now.

T = 4.2x10³ K

With this limited information, this data seems to suggest at some point of Moon's history, it could have been very hot (T = 4.2x10³ K) which causes water molecules to escape then. As the Moon cools, not enough water molecules was able to form on the Moon's surface to form oceans like what we have on Earth.

7.3.8.6.3 Model ϕ

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/63

 

Translations

Code	Language		Translator	Run

Credits

lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); andrew duffy

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity11/gravity11_Simulation.xhtml 

 

Briefing Document: 🚀Earth-Moon Escape Velocity Simulation

1. Overview:

This document analyzes a resource focusing on a JavaScript HTML5 applet simulation model designed to illustrate the concepts of gravitational potential and escape velocity, specifically in the context of the Earth-Moon system. The resource is part of the Open Educational Resources / Open Source Physics @ Singapore initiative. It aims to provide an interactive and inquiry-based learning experience for students.

2. Main Themes:

• Gravitational Potential: The simulation emphasizes the concept of gravitational potential (ϕ) as a scalar quantity and how the total potential at a point is the sum of individual potentials due to multiple masses.
• Quote: "The total ϕ at a point in a field due to two or more source masses is the scalar addition of the individual ϕ due to each mass at that point, i.e. . ϕtotal = ∑ϕ"
• Escape Velocity: A core focus of the resource is understanding the escape velocity – the minimum speed required for an object to permanently escape a gravitational field.
• Quote: "There is a critical speed at which an object can be launched such that it can escape the Earth permanently. Such a critical speed is termed as the escape speed."
• Conservation of Energy: The simulation uses the principle of conservation of energy to derive the escape velocity. It assumes that at an infinite distance from the Earth, both kinetic and potential energy are zero.
• Interactive Learning: The resource advocates for active, learner-centered inquiry through simulation, allowing students to "experience" escape velocity by manipulating parameters.
• Application of Concepts: The document covers applications, including calculating escape velocities for both Earth and the Moon, as well as connecting to root-mean-square speed of gases to deduce the likely temperature of the Moon in the past.

3. Key Ideas and Facts:

• Gravitational Potential Summation: The total gravitational potential at any point in space is the scalar sum of all individual gravitational potentials at that point created by the masses generating those fields. The document clarifies that potential energy follows suit.
• Escape Velocity Defined: The escape velocity is the minimum speed an object must attain to overcome a gravitational pull. An object launched at this speed will not return to Earth. The resource emphasizes the point that “what goes up may come down,” not must come down, contingent upon velocity.
• Earth Escape Velocity: The escape velocity from the Earth's surface is calculated to be 1.12 x 104 m/s (or 11.2 km/s).
• Quote: "Therefore, to escape from Earth, it implies that the projectile must have a minimum launch velocity of v = 1.12x104 m/s ."
• Moon Escape Velocity: The escape velocity from the Moon's surface is calculated to be 2400 m/s.
• Quote: "Answer: vescape Moon=2400 m/s"
• Simulation-Based Inquiry: The resource provides instructions on using the simulation to explore escape velocity, encouraging students to:
• Remove the effects of the moon
• Observe the test mass starting from the Earth's surface
• Experiment with different launch velocities to determine the minimum speed for escape.
• Historical Temperature of the Moon: Using the derived escape velocity for the moon, and the root-mean-square speed of gases, an estimation for the historical surface temperature of the Moon is calculated at 4.2 x 103 K which would explain the lack of water on the moon. This illustrates application of multiple concepts in concert.
• Quote: "With this limited information, this data seems to suggest at some point of Moon's history, it could have been very hot (T = 4.2x103 K) which causes water molecules to escape then. As the Moon cools, not enough water molecules was able to form on the Moon's surface to form oceans like what we have on Earth."
• Educational Application: The applet is designed for Junior College (high school) physics students, utilizing a technology-enhanced inquiry-based approach. It focuses on developing students' abilities to apply physics principles, collect and analyze data, and synthesize their understanding.
• Quote: "The lesson was tested & carried out with JC1 as a research on physics by inquiry using simulations."
• Teacher's Role: The role of the teacher is to be a "technology, content, pedagogy and knowledge expert" who facilitates the students' exploration and understanding of the scientific concepts.
• Quote: "Strategies Teacher as technology, content, pedagogy and knowledge expert (TPCK), facilitating the inquiry learning process, with teacher to facilitate at suitable times."

4. Intended Use and Pedagogy:

The simulation is intended to be used in a virtual laboratory environment. The teaching methodology is focused on active learner-centered learning with a heavy emphasis on inquiry. Teachers are positioned to help students achieve the intended learning outcomes in these active learning scenarios. It’s an open resource where the students are provided with computers.

5. Technical Details:

• Platform: The applet is a JavaScript HTML5 application, compatible with various devices.
• Quote: "Android/iOS including handphones/Tablets/iPads", "Windows/MacOSX/Linux including Laptops/Desktops", "ChromeBook Laptops"
• Accessibility: The applet is accessible via a provided URL and can be embedded in web pages.
• Development: The simulation was created using Easy JavaScript Simulation (EJS), a tool designed for building interactive physics simulations.

6. Additional Resources:

The document also provides links to related resources, including:

• A Java version of the simulation
• Geogebra resources created by other educators
• Various other interactive simulations developed by the same initiative

7. Conclusion:

This resource offers a valuable tool for teaching complex physics concepts in an engaging and interactive way. By using simulation and inquiry-based learning, it promotes a deeper understanding of gravitational potential, escape velocity, and their implications for the Earth-Moon system. The provided applet and approach are well-suited for use in a high school physics classroom, particularly in a 1-to-1 computing environment.

 

Versions:

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar by Todd TimberLake and lookang Java version

Video

https://notebooklm.google.com/notebook/be355cf6-d4fa-429b-aff1-344340f038c3/audio

Other resources

https://www.geogebra.org/m/va3dbqyd by Seng kwang

Writeup ICT

Virtual Laboratory Gravitational Field & Potential of Earth and Moon

Resources

  https://www.geogebra.org/m/va3dbqyd by Tan Seng Kwang

Earth-Moon Escape Velocity Study Guide

Quiz

Answer the following questions in 2-3 sentences each:

1. What does the term "escape speed" refer to in the context of launching an object from a celestial body?
2. How is the total gravitational potential at a point calculated when considering multiple source masses, like the Earth and Moon?
3. In the provided simulation, what are the initial conditions for testing the escape velocity of a projectile from Earth?
4. What is the theoretical escape velocity of an object launched from the Earth's surface, according to the text?
5. What is the theoretical escape velocity of an object launched from the Moon's surface?
6. Briefly describe the relationship between root-mean-square speed of gas particles and temperature, and how that relates to the Moon's history.
7. How can the provided simulation be used to explore the concept of escape velocity?
8. According to the text, what are some of the ICT tools used in conjunction with the study of gravitational fields?
9. How does the text advocate for a technology-enhanced, active learning approach to physics?
10. How does the text connect escape velocity to the historical lack of water on the moon?

Quiz Answer Key

1. Escape speed refers to the critical speed at which an object must be launched to overcome a celestial body's gravitational pull and escape permanently, never returning to the surface. This speed is such that the object’s kinetic energy and potential energy sum to zero.
2. The total gravitational potential at a point due to multiple masses is found by scalar addition of the individual gravitational potentials due to each mass at that point. This implies that the net potential is simply the sum of each individual contribution.
3. In the simulation, the initial conditions for testing Earth’s escape velocity involve placing a test mass on the Earth's surface, setting its initial velocity, and then observing its trajectory. The default Earth Surface view places the test mass on the right side.
4. The text states that the theoretical escape velocity for an object launched from the Earth's surface is 1.12 x 10^4 m/s, or 11,200 m/s.
5. The theoretical escape velocity for an object launched from the Moon's surface is 2400 m/s, or 2.4 x 10^3 m/s.
6. The root-mean-square speed of gas particles is directly related to the temperature; as temperature increases, so does the speed of the particles. The text indicates that, at some point, the Moon's surface was so hot that the root-mean-square speed of water molecules exceeded the moon's escape velocity, preventing the accumulation of water.
7. The simulation can be used to explore escape velocity by setting the initial velocity of a test mass and observing whether it is able to escape the gravitational pull of a celestial body; the user is prompted to find the minimum velocity for escape by experimentation.
8. The text uses computers with Java Runtime installed, along with Ejs Open Source Gravitational Field & Potential Java Applet for the study of gravitational fields. The simulations were intended for use with desktop or laptop computers, as well as mobile devices.
9. The text advocates for active, learner-centered learning by using technology, particularly simulations, to enable students to explore and discover scientific concepts, with the teacher acting as a facilitator. This includes student-led planning, data collection, analysis, evaluation, and synthesis of information.
10. The text suggests that the Moon may have been extremely hot in its early history. The high temperature gave the water molecules sufficient kinetic energy to surpass the escape velocity, thus preventing the formation of oceans.

Essay Questions

Answer these questions in a well-developed essay format:

1. Discuss the concept of gravitational potential and how it relates to the total potential energy of a system, using the Earth-Moon system as an example.
2. Explain the concept of escape velocity, and how it is calculated, emphasizing the role of conservation of energy. Analyze how the simulation model described in the text helps in visualizing this concept.
3. The text provides a scenario about the Moon's surface temperature and its implications for the presence of water. Using root-mean-square velocity and escape velocity, evaluate the role of kinetic theory in explaining the moon's current state.
4. The text suggests an inquiry-based approach to teaching physics using simulations. Evaluate the benefits and challenges of using such an approach in a classroom setting.
5. Analyze the connection between the development of educational simulations and technological progress in learning, using examples from the provided text.

Glossary of Key Terms

• Gravitational Potential (ϕ): A measure of the potential energy per unit mass at a specific location in a gravitational field. The total potential at any given location due to multiple source masses is the scalar sum of the potentials due to each mass separately.
• Escape Speed/Velocity: The minimum speed required for an object to overcome the gravitational pull of a celestial body and move infinitely far away, without any additional thrust.
• Kinetic Energy (KE): The energy an object possesses due to its motion.
• Potential Energy (PE): The energy stored in an object due to its position or configuration. In the context of gravity, this refers to the energy an object has due to its location within a gravitational field.
• Conservation of Energy: The principle that the total energy of an isolated system remains constant; energy can neither be created nor destroyed, but it can be transformed from one form to another.
• Root-mean-square Speed (vrms): A measure of the average speed of particles in a gas, taking into account their different velocities. It is calculated as the square root of the average of the squares of the particles' speeds.
• Molar Gas Constant (R): A fundamental physical constant that is used in thermodynamics.
• Molar Mass (Mm): The mass of one mole of a substance.
• Scalar Addition: A method of adding quantities that have magnitude but no direction; numbers can be directly added.
• Inquiry Approach: An educational method where students learn by asking questions and performing experiments rather than memorizing facts. In this context, students use the simulation to discover the physics principle at work.
• ICT (Information and Communication Technology): Technologies used to transmit, manipulate, and store data, often used to enhance education.

FAQ

• What is gravitational potential and how does it relate to potential energy?
• Gravitational potential (ϕ) at a point is a scalar value representing the amount of potential energy per unit mass an object would have at that point due to gravity. The total gravitational potential at a location due to multiple masses is the scalar sum of the individual potentials from each mass. The potential energy (PE or U) of an object is then the mass (m) of that object multiplied by the total gravitational potential at its location, i.e., PE = mϕ.
• How is the total gravitational potential calculated when considering multiple bodies like the Earth and Moon?
• The total gravitational potential at any point is calculated by summing the individual gravitational potentials caused by each body. For example, if you are considering the Earth and Moon, the total potential (ϕtotal) at a given location is the sum of the gravitational potential due to the Earth (ϕ2) and the gravitational potential due to the Moon (ϕ1): ϕtotal = ϕ1 + ϕ2. This is a scalar addition.
• What is escape velocity and what does it mean for an object to reach it?
• Escape velocity is the minimum speed an object must achieve to escape a celestial body's gravitational pull permanently. If an object is launched at a speed equal to or greater than the escape velocity, it will never return to the surface, assuming no other forces act on it. The minimum speed of 0 is assumed at infinite distance away. For Earth, this speed is approximately 1.12 x 10^4 m/s, and for the Moon, it's around 2400 m/s.
• How is the escape velocity determined from the principle of energy conservation?
• Escape velocity is derived by equating the kinetic energy and potential energy of an object on the surface of a celestial body to zero kinetic and potential energy at infinite distance. Using the principle of conservation of energy, and assuming the minimum speed is 0 at infinite distance, we have the object's initial kinetic energy (1/2mv^2) plus its initial potential energy (-GMm/r) equaling zero. This allows us to solve for the escape velocity 'v'.
• How can I investigate escape velocity using the simulation provided?
• The simulation allows you to manipulate parameters to test the escape velocity. First, remove the effects of the Moon. You can place a test mass on the surface of the Earth and key in a velocity for the test mass. Then press "play". By adjusting the velocity you can observe if the mass escapes or fails to escape the Earth's gravitational pull. By running multiple trials you can find the minimum theoretical speed to escape Earth's pull by iteration. Similarly, you can test escape velocities for the Moon using the simulation.
• Why does the Moon not have significant surface water like Earth?
• Based on the escape velocity of the Moon and kinetic theory of gases, it's theorized that the Moon may have once had a surface temperature as high as 4.2x10^3 K. At these high temperatures, water molecules would have possessed root-mean-square speeds exceeding the Moon's escape velocity. Consequently, they escaped into space, preventing the formation of oceans. As the Moon cooled, not enough water molecules formed to form oceans.
• What learning objectives are covered using this simulation and its related materials?
• The lesson plan using the simulation focuses on a learner-centered, inquiry-based approach to learning. The learning objectives include:

1. Students will be able to apply the equation g = GM/r^2 for the gravitational field strength of a point mass to new situations and solve related problems.
2. Students will be able to solve problems using the equation φ = -GM/r for the potential in the field of a point mass. The activities include students designing their own experiment, making observations, collecting data, and proposing and verifying their hypothesis of the physics principle.

• What is the pedagogical approach that is promoted by the simulation?

The pedagogical approach is active learner-centered learning, with a teacher facilitating the inquiry learning process. This promotes TPCK (technology, pedagogy, content and knowledge) skills, which include self-directed planning, data collection, analysis, and synthesis of scientific knowledge. Teachers are encouraged to serve as facilitators, guiding students in their exploration of the physics concepts. The simulation encourages a hands-on approach to understanding complex phenomena.