About

7.3.8.4 Example 9 (J89/II/2)

7.3.8.4.1 Values for the gravitational potential due to the Earth are given in the table below.

Distance from Earth’s surface / m	Distance from Earth’s centre / m	Gravitational potential / MJ kg-1	Gravitational Field Strength g / ms-2	Rate of change of potential with distance  $\genfrac{}{}{0.1ex}{}{d\varphi }{dr}$/ ms-2
0	6 370 000 = 6.37x106= 0.637x107	-62.72
	10 000 000 = 1.0x107	-40.10
1.363x107	2.0x107	-20.00
	3.0x107	-13.34	-0.44	0.44
	4.0x107	-10.01
	5.0x107	-8.01	-0.16	0.16
	Infinity	0

(i) given that radius of Earth = 6370 km, fill in the missing values in the column of Distance from Earth’s surface / m.

(ii)    Calculate the change in potential if an object travels from r = 5.0x10⁷ m to r = 2.0x10⁷ m

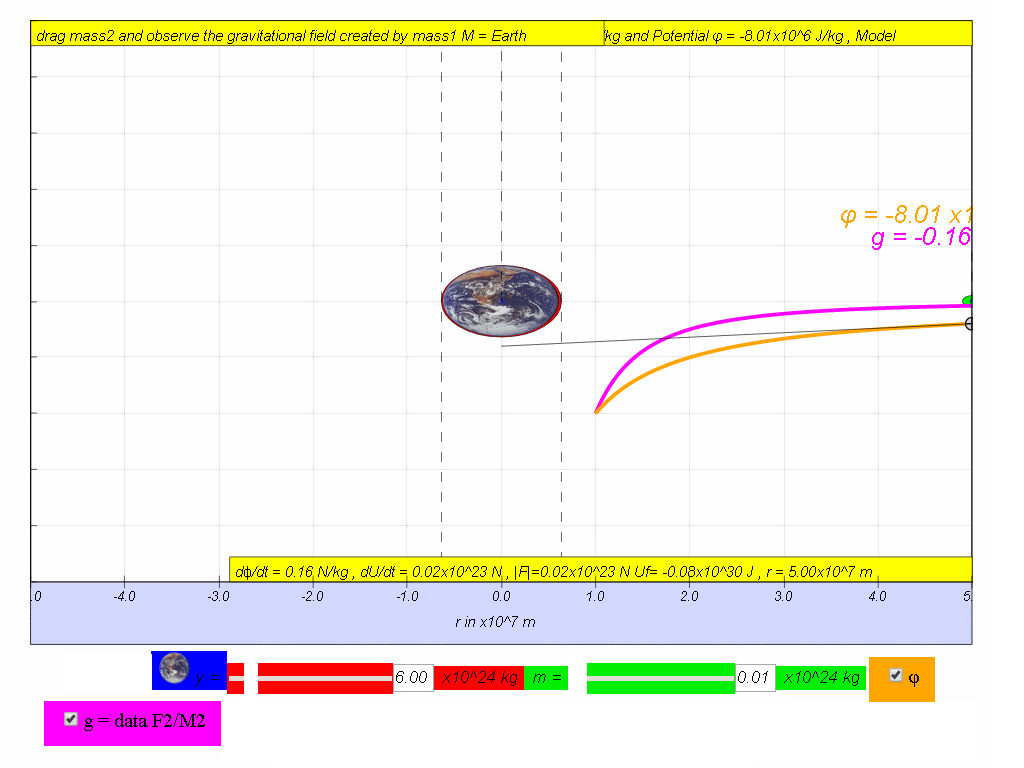
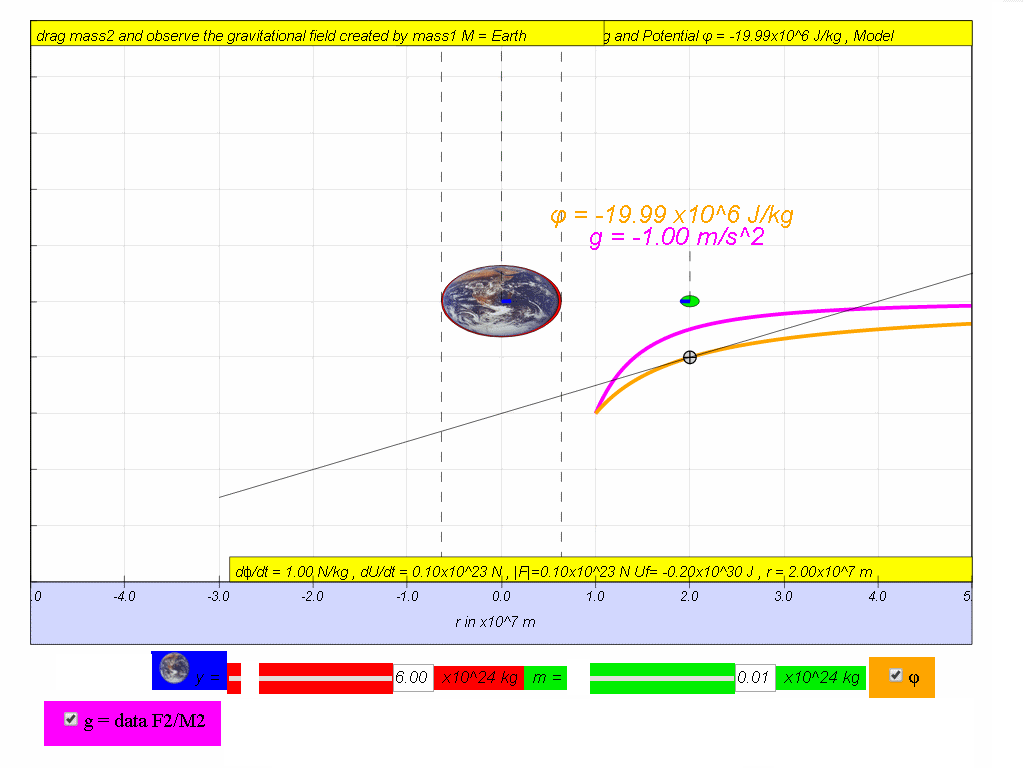
Answer: Δϕ = ϕfinal - ϕinitial = -20.00x10⁶ - (-8.01x10⁶) = -11.95x10⁶ J/kg

(iii) Hence or otherwise, calculate the change in potential energy if the object-satellite has a mass 0.01x10²⁴ kg.

Answer:  ΔPE = ΔU = m(Δϕ) = 0.01x10²⁴(-11.95x10⁶) = -1.196x10²⁹ J = -0.20x10³⁰ J

(iv) Determine the potential energy lost by object-satellite of 0.07x10²⁴ kg from a height of 13 630 000 to the Earth's surface.

Answer: ΔPE = m(Δϕ) = 0.07x10²⁴ (-6.67x10-11)(6.0x10²⁴)($\frac{1}{\left(6.37x10^6\right)}-\frac{1}{(13630000+6.37x10^6)}$ ) = (0.07x10²⁴ )(-6.27x10⁷ -(-20.00x10⁷))= (0.07x10²⁴ )(-4.28x10⁷ ) = 2.996x10³⁰ = 3.00x10³⁰ J

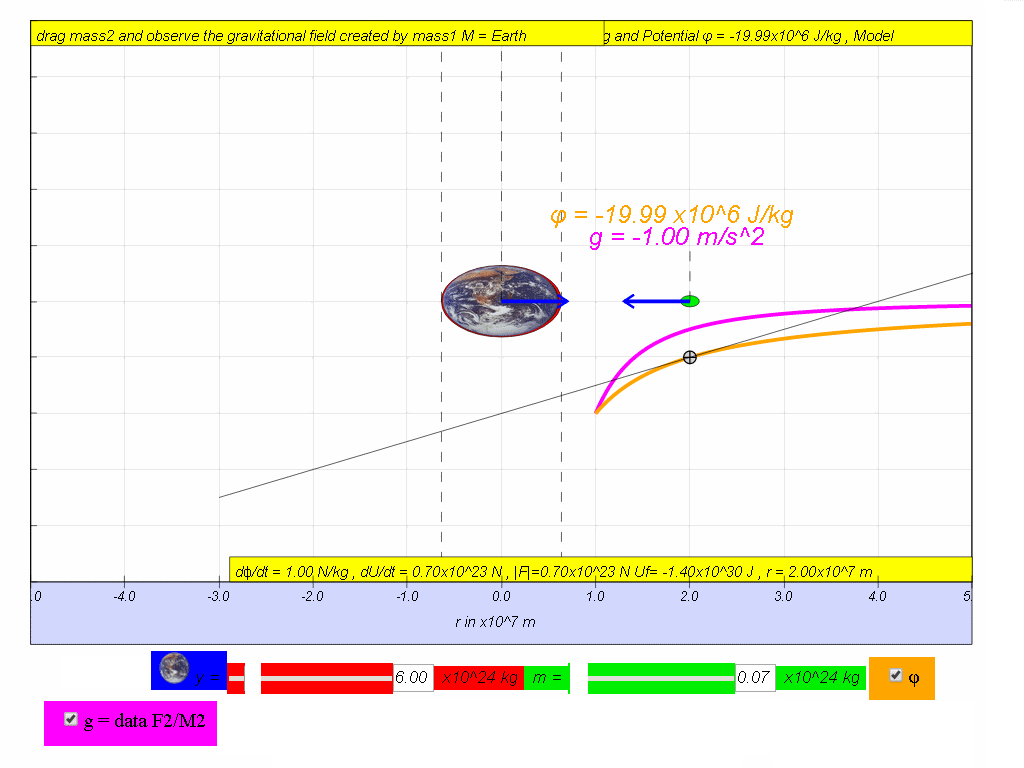
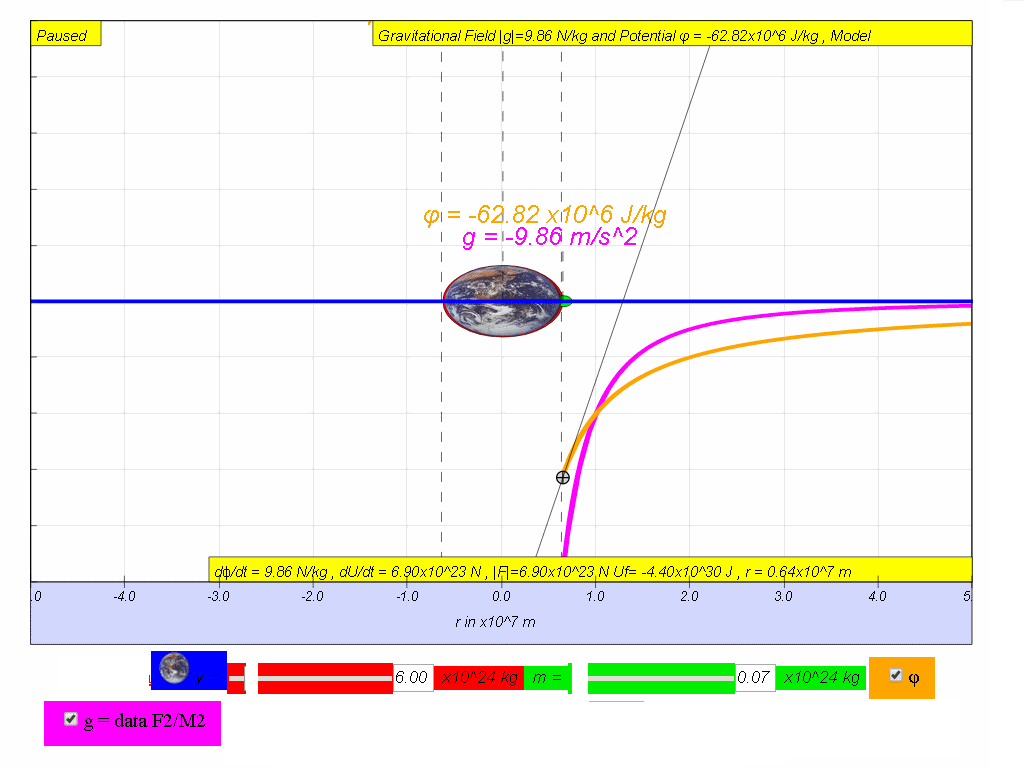
v) by means of using the simulation, move the mass and record down and fill in the last 2 missing columns for Gravitational Field Strength and  rate of change of potential with distance. 

vi) Hence, suggest a relationship between g, ϕ and r.

vii) Explain why the accuracy of determining g at r = 3x10⁷ is poor when using the following values at r = 2x10⁷ and 4x10⁷ m where $\genfrac{}{}{0.1ex}{}{d\varphi }{dr}=-\frac{-10.01-\left(20.00\right)}{4x10^7-2x10^7}$

7.3.8.4.2 Model

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/60

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity07_1/gravity07_1_Simulation.xhtml 

Briefing Document: 🍎Gravitational Field and Potential Earth Simulation Model

1. Introduction

This document provides a review of the "7.3.8.4 Gravitational Field and Potential Earth JavaScript HTML5 Applet Simulation Model" resource found on the Open Educational Resources / Open Source Physics @ Singapore website. The resource is designed as an interactive tool to help users understand concepts related to gravitational fields, potential, and their relationships. It is an example of an EasyJavaScriptSimulation (EJS) applet, which is designed to run on a variety of devices.

2. Key Themes and Concepts

• Gravitational Potential: The resource centers around the concept of gravitational potential, denoted by ϕ, which represents the potential energy per unit mass at a given point in a gravitational field. The simulation and included table provide values of gravitational potential at various distances from the Earth's center.
• Gravitational Field Strength: The model also explores the gravitational field strength, denoted by 'g', which is the force per unit mass exerted on an object by a gravitational field. The simulation allows users to observe and measure the value of 'g' at different distances.
• Relationship between Potential and Field Strength: A key learning objective is to help users understand how the gravitational potential and the field strength are related. The simulation and questions implicitly guide users toward understanding that the gravitational field strength is related to the rate of change of potential with distance.
• Potential Energy: The model enables calculation of the change in potential energy of an object as it moves within the Earth's gravitational field. This helps reinforce the concepts of energy conservation and work done by gravity.
• Interactive Simulation: The resource is an interactive HTML5 applet, encouraging users to directly explore the concepts by manipulating parameters and observing the outcomes.

3. Key Facts and Ideas

• Data Table: The resource includes a data table that provides pre-calculated values for gravitational potential (ϕ) and distances from the Earth's surface and center. This table is used as the foundation for various calculations and questions. For example, the table begins with the radius of the earth and then gives potential values at increasing distances out from the earth's center.
• Calculations: The resource presents several exercises involving the calculations of changes in potential and potential energy. Here are some examples of such calculations, with original source quotes:
• (ii) Calculation of change in potential: "Calculate the change in potential if an object travels from r = 5.0x107 m to r = 2.0x107 m Answer: Δϕ = ϕfinal - ϕinitial = -20.00x106 - (-8.01x106) = -11.95x106 J/kg"
• (iii) Calculation of change in potential energy: "Hence or otherwise, calculate the change in potential energy if the object-satellite has a mass 0.01x1024 kg. Answer: ΔPE = ΔU = m(Δϕ) = 0.01x1024(-11.95x106) = -1.196x1029 J = -0.20x1030 J"
• (iv) Calculation of potential energy lost: "Determine the potential energy lost by object-satellite of 0.07x1024 kg from a height of 13 630 000 to the Earth's surface. Answer: ΔPE = m(Δϕ) = 0.07x1024 (-6.67x10-11)(6.0x1024)( 1 ( 6.37 x 1 0 6 ) - 1 ( 13630000 + 6.37 x 1 0 6 ) ) = (0.07x1024 )(-6.27x107 -(-20.00x107))= (0.07x1024 )(-4.28x107 ) = 2.996x1030 = 3.00x1030 J"
• Simulation Interaction: Users are prompted to "move the mass and record down and fill in the last 2 missing columns for Gravitational Field Strength and rate of change of potential with distance," using the simulation directly. This implies an interactive component to the applet, allowing users to see these values dynamically.
• Relating g, ϕ and r: The questions implicitly encourage students to understand that gravitational field strength (g) is the negative gradient of gravitational potential ( dϕ/dr ) as well as that g is related to distance (r).

4. Learning Objectives

Based on the content, the primary learning objectives of this resource are:

• To define and understand gravitational potential (ϕ) and gravitational field strength (g).
• To calculate changes in gravitational potential as an object moves within a gravitational field.
• To relate changes in gravitational potential to changes in potential energy.
• To understand the relationship between gravitational potential, field strength, and distance from the center of a gravitational source.
• To use an interactive simulation to visualize and explore these concepts.

5. Target Audience

The resource is explicitly labeled for "Junior College," placing the target audience at the pre-university level. The inclusion of calculations and the request to "suggest a relationship between g, ϕ and r" indicate that users are expected to have some prior knowledge of physics principles, but still need to consolidate their understanding through interactive engagement.

6. Technical Aspects

• HTML5 Applet: The resource is delivered as an HTML5 applet, making it accessible on a wide range of devices (including desktop, laptops, and mobile devices).
• EasyJavaScriptSimulation (EJS): The simulation is created with EJS, which is described as a framework for creating interactive simulations. EJS is open-source, implying that teachers and users might be able to modify or extend the existing simulations or make their own simulations with the framework.
• Accessibility: The resource is intended to be accessible on various operating systems (Windows/MacOSX/Linux) and devices, including "handphones/Tablets/iPads". The inclusion of specific browsers ("ChromeBook Laptops") indicate a focus on wider reach.

7. Additional Notes

• The site uses the term "object-satellite" throughout the text, which is a bit unusual. While any object in a gravitational field can be considered a satellite, the term is most often used for objects orbiting a planet or star.
• The resource is provided by Open Educational Resources / Open Source Physics @ Singapore. The text provides an email address for further inquiries and also directs those seeking commercial use of the underlying EJS library to a separate website and contact. The creative commons license for the content is explicitly noted as Creative Commons Attribution-Share Alike 4.0 Singapore License.

8. Conclusion

The "Gravitational Field and Potential Earth JavaScript HTML5 Applet Simulation Model" provides a valuable interactive tool for students to explore the fundamental concepts of gravitational potential and field strength. The resource, through its interactive simulation, data, and calculation questions, facilitates a deeper understanding of these important physics concepts and how they are related, targeting a pre-university audience.

Gravitational Fields and Potential Study Guide

Quiz

Answer the following questions in 2-3 sentences each:

1. What does the term "gravitational potential" refer to?
2. Explain how gravitational potential changes as you move further away from the Earth.
3. What is the relationship between gravitational potential energy and gravitational potential?
4. According to the data table, what is the gravitational potential at the surface of the Earth?
5. How is gravitational field strength related to the rate of change of potential with distance?
6. If an object moves from a location with a higher potential to one with a lower potential, what happens to its potential energy?
7. Why is calculating gravitational field strength using values from distant points less accurate?
8. What does the simulation provided in the source allow you to explore and visualize?
9. What are the units of gravitational potential in the provided data table?
10. What is the significance of the negative sign in the values of gravitational potential and potential energy?

Quiz Answer Key

1. Gravitational potential is the amount of work required to move a unit mass from an infinite distance to a specific point in a gravitational field. It is a scalar quantity and a property of the gravitational field itself.
2. As you move further away from the Earth, the gravitational potential increases. This indicates that less work is required to move a mass from infinity to that point.
3. Gravitational potential energy is the product of the mass of an object and the gravitational potential at its location. Thus, potential energy is the mass-dependent expression of the field's potential.
4. According to the data table, the gravitational potential at the surface of the Earth is -62.72 MJ/kg. This indicates the lowest potential value in the table.
5. Gravitational field strength is equal to the negative rate of change of gravitational potential with respect to distance, therefore it's represented by the slope of the potential-distance graph.
6. If an object moves from a higher potential to a lower potential, its potential energy decreases. This energy is typically converted into kinetic energy, causing the object to move towards the source of gravity.
7. Calculating gravitational field strength using values from distant points is less accurate because the rate of change of potential can vary significantly over larger distances, reducing the approximation of the slope.
8. The simulation allows users to visually explore the relationship between gravitational potential, distance from Earth, and the effect of changing the position of a mass in the field.
9. The units of gravitational potential in the provided table are MJ/kg, which stands for megajoules per kilogram.
10. The negative sign indicates that the gravitational potential and potential energy are defined as zero at infinity. Since the field strength does work in moving the mass towards the Earth, energy must be removed from the system.

Essay Questions

1. Discuss the relationship between gravitational potential, gravitational potential energy, and gravitational field strength. How are these concepts interconnected, and how do they vary with distance from a celestial body like Earth?
2. Using the data provided in the table, analyze the changes in gravitational potential as you move away from Earth’s surface. What inferences can you make about the nature of the gravitational field based on these changes?
3. Explain how the simulation tool can be used to enhance understanding of gravitational concepts. How does visualizing these phenomena aid in comprehending abstract physics ideas?
4. Consider the implications of using a finite difference method to calculate the field strength. What are the limitations when you measure changes in potential over greater distances?
5. Imagine you are designing a satellite mission. How would you use your understanding of gravitational potential to manage the satellite’s energy and orbital path?

Glossary of Key Terms

• Gravitational Potential: The work done per unit mass to move an object from infinity to a specific point in a gravitational field. It is a scalar quantity, measured in Joules per kilogram (J/kg).
• Gravitational Potential Energy: The energy an object possesses due to its position in a gravitational field. It is the product of an object's mass and the gravitational potential at its location, measured in Joules (J).
• Gravitational Field Strength: The force experienced by a unit mass placed in a gravitational field, equivalent to the acceleration due to gravity. It is a vector quantity, measured in meters per second squared (m/s²).
• Rate of Change of Potential with Distance: The change in gravitational potential per unit change in distance. It is related to the gravitational field strength, as the negative gradient of the potential.
• Finite Difference Method: An approach to approximating the derivative (rate of change) of a function using values from two nearby points instead of infinitesimal points.
• Simulation Model: A computer program that represents a physical system or process. Used in this context to visualize the gravitational field and how it impacts the movement of a mass.
• Scalar Quantity: A physical quantity that has magnitude but no direction, such as gravitational potential.
• Vector Quantity: A physical quantity that has both magnitude and direction, such as gravitational field strength.

 

Video

https://notebooklm.google.com/notebook/7f55f128-3649-4b95-b40f-df06a5cd9dc9/audio

Versions

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar

 

Cast of Characters

• Loo Kang Wee (lookang): This is likely the main curator or a key contributor to the Open Educational Resources / Open Source Physics @ Singapore platform, as his username is associated with site user info. He appears to be involved in developing and promoting various simulations and educational resources.

Frequently Asked Questions on Gravitational Fields and Potential

1. What is gravitational potential, and how is it measured in the context of this simulation? Gravitational potential is the amount of work required to move a unit mass from an infinite distance to a specific point in a gravitational field. In this simulation, it's given in units of MegaJoules per kilogram (MJ/kg) and is measured at various distances from the Earth's center. A higher (less negative) value indicates a weaker gravitational potential at that point, where less energy is required to move an object there from infinity. It decreases (becomes more negative) closer to the Earth.
2. How does gravitational potential relate to potential energy? The change in potential energy (ΔPE) of an object is directly proportional to the change in gravitational potential (Δϕ). It's calculated using the formula ΔPE = m * Δϕ, where 'm' is the mass of the object. In essence, a change in gravitational potential as an object moves within a gravitational field translates to a corresponding change in the object’s potential energy.
3. How do you calculate the change in gravitational potential when an object moves between two points in a gravitational field? The change in potential (Δϕ) is calculated by subtracting the initial gravitational potential (ϕinitial) from the final gravitational potential (ϕfinal): Δϕ = ϕfinal - ϕinitial. For example, if an object moves from a location with a potential of -8.01 MJ/kg to a location with a potential of -20.00 MJ/kg, the change in potential would be -11.99 MJ/kg. This negative change indicates the potential decreases in the direction closer to the planet.
4. What is the relationship between gravitational field strength (g) and gravitational potential (ϕ)? The gravitational field strength (g) is the rate of change of gravitational potential with respect to distance. In other words, g is the negative gradient of gravitational potential. Mathematically this means g = - dϕ/dr, where dϕ/dr is the rate of change of potential with respect to radial distance. A steeper gradient in potential indicates a stronger gravitational field, so higher absolute g values are near the planet and lower values are far away.
5. How can I determine the gravitational field strength (g) using the provided data on gravitational potential? The gravitational field strength (g) can be determined by finding the rate of change of gravitational potential with distance using the simulation. To calculate this, find the change in gravitational potential (Δϕ) between two points and divide it by the change in distance (Δr) between those two points. This gives an approximate value for 'g' in ms-2. Note that this calculation is less accurate when using values very far apart due to the gradient not being linear.
6. Why might the accuracy of calculating ‘g’ be poor when using potential values at large distance intervals? The accuracy of calculating ‘g’ is poor when using values at large intervals because the rate of change of potential with distance is not constant. The relationship is nonlinear. Using points further apart gives an average field strength over that distance, not the instantaneous field strength at a single point. Therefore, using smaller intervals and using the simulation tools will result in more precise value of gravitational field strength at a point.
7. How does this simulation help visualize and understand the relationship between gravitational potential, field strength, and distance? The simulation allows you to move a mass within the gravitational field of the earth and dynamically observe the changes in gravitational potential, field strength and distance of the mass. Through this movement and visual feedback, the non-linear relationship between them can be observed and studied, enhancing understanding of the nature of the concepts.
8. What are some practical applications or uses of understanding gravitational potential and field strength beyond theoretical physics? Understanding gravitational potential and field strength is crucial for various applications, including:

• Satellite Launches and Orbits: Calculating the energy needed to put satellites into orbit and maintaining those orbits.
• Spacecraft Navigation: Planning trajectories for spacecraft and understanding gravitational influences of planets.
• Geophysics: Studying the Earth’s gravitational field to learn about the density of the Earth's crust and mantle and other features.
• Global Positioning Systems (GPS): Compensating for variations in the gravitational field to ensure accurate location data.
• Energy Calculations: Determining energy changes associated with moving objects within a gravitational field.