About

7.3 Gravitational Potential Energy (symbol: U and units: J)

7.3.1 in Work, Energy & Power topic

In the topic of Work, Energy & Power, the calculation of gravitational potential energy (GPE) is determined using the expression, mgh, which assumes that the gravitational field strength g is roughly constant, but a more robust formula is required for varying field strength, say when sending rockets which travel into outer space from the surface of the Earth.

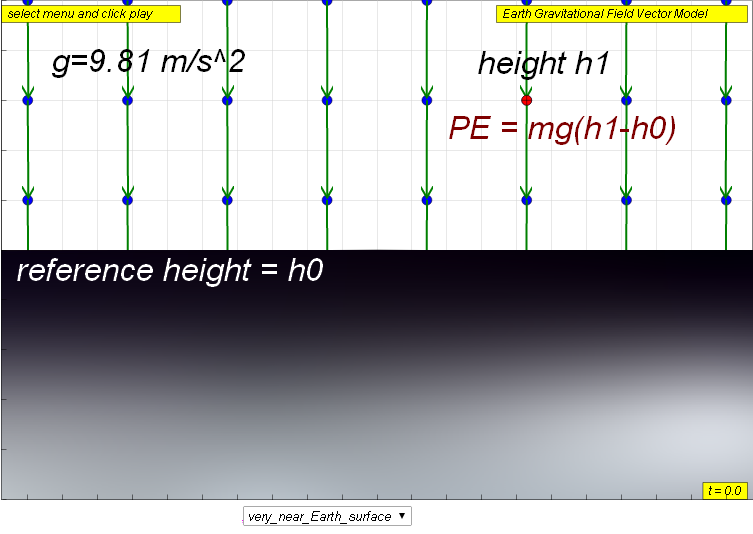
ΔU = ΔPE = mgh or mgΔh

where ΔPE or ΔU is the gravitational potential energy possessed by mass m measured from the reference height h₀ , g is the gravitational field strength created by source mass M.

h or Δh is the change in the height (h₁ - h₀ ) of the mass m.

7.3.2 more universal formula for Potential energy

This formula PE = mgh or mgΔh was appropriate when the magnitude of gravitational field strength, g of Earth was assumed to be constant (9.81 m s^-2) over this height. When the assumption of constant gravitational field strength is not valid, a more robust PE formula is given by the calculation of potential energy 

$U=-m\frac{GM}{r}$

where

U is the gravitational potential energy possessed by mass m measured from the reference position of infinity,

G is the gravitational constant, approximately 6.673×10⁻¹¹ N·(m/kg)²,

M is the source mass that sets up the gravitational field,

m is the test mass experiencing the gravitational field set up by M, and

r is the distance away from the centre of the gravitational field source mass M

$$

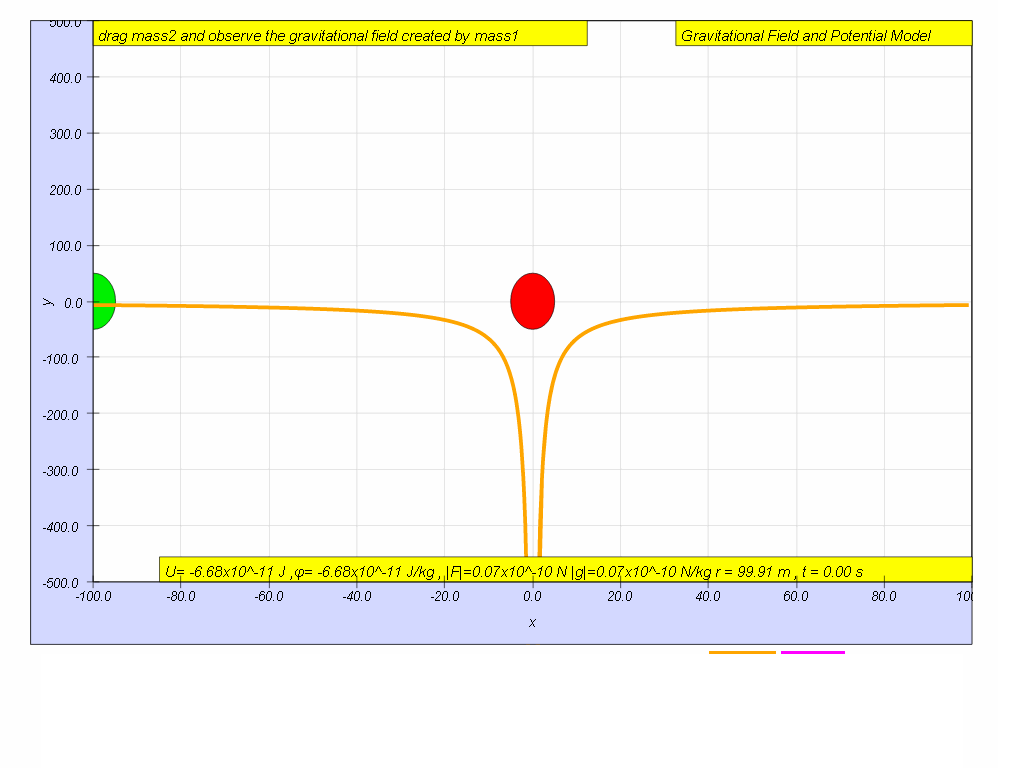
In this particular case, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}=-(1)\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(100\right)}{100}=-6.67x10^{-11}J$

Calculate for the case when r = 50 m.

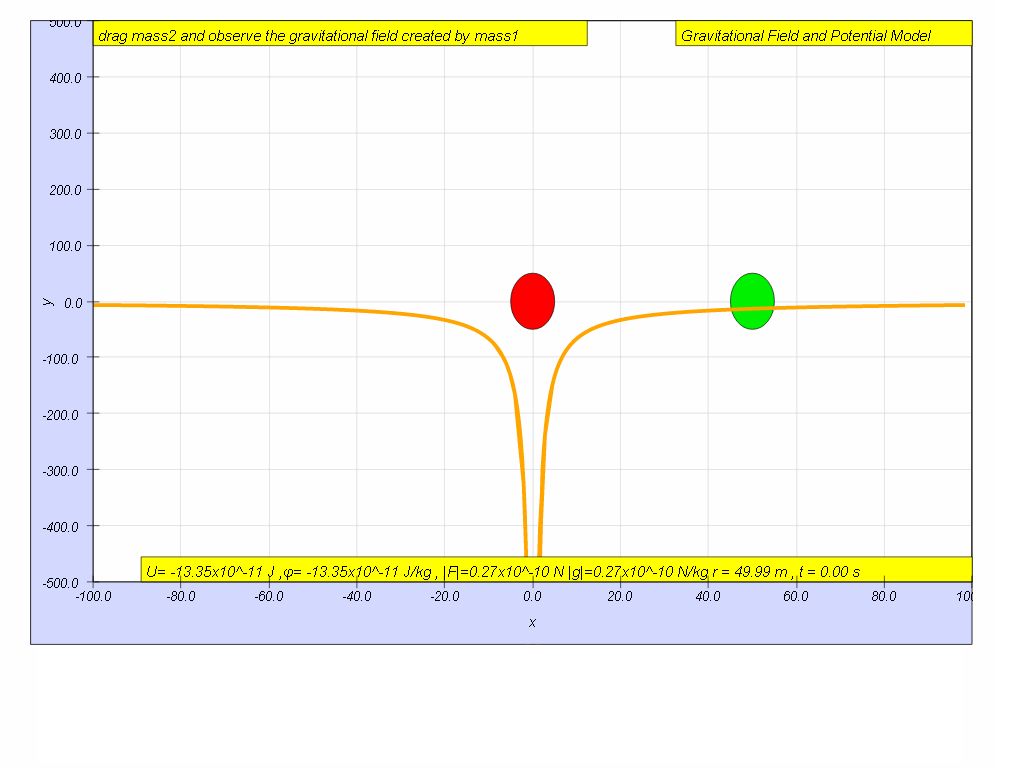
Similarly, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}=-(1)\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(100\right)}{50}=-13.35x10^{-11}J$

7.3.3 Characteristics of Gravitational potential energy

equation is given by $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$

a scalar quantity (i.e. it has no direction only magnitude )

has only negative value due to the reference potential equal zero U = 0, position is defined at position r = infinity,  ∞, and gravity is attractive which means the lowest potential position is at the centre of the source mass M.

U = -infinity, at r = 0, lowest potential energy

U = 0, at r = infinity, highest potential energy   

Now, this leads to the need to define gravitational potential energy.

7.3.4 Definition of gravitational potential energy, U

The gravitational potential energy (U) of a mass m at a point (due to the gravitational field set up by mass M ) is defined as the work done by an external agent in bringing the mass from infinity to that point r distance away from source mass M.

To further understand the meaning of this definition, let's start with the definition for work done on external agent, where WD = WD _{by external agent}.

$WD=\underset{\infty }{\overset{r}{\int }}Fdx$
$$Substituting the formula for force F and working out the integration, it can be shown.

$WD=\underset{\infty }{\overset{r}{\int }}Fdr=\underset{\infty }{\overset{r}{\int }}\genfrac{}{}{0.1ex}{}{GMm}{r^2}$ $dr={\left[\frac{-GmM}{r}\right]}_r^{\infty }=[\genfrac{}{}{0.1ex}{}{-GmM}{r}-\genfrac{}{}{0.1ex}{}{-GmM}{\infty }]=-\genfrac{}{}{0.1ex}{}{GmM}{r}$

Notice the formula for this work done by external agent is equal to the U.

$WD=U=-\frac{GmM}{r}$

To understand this definition, we can use the simulation with some imagination.
Imagine the test mass, m is at a distance r = ∞, U_∞ = 0 (the simulation does not allow r = ∞, but let's assume r = 100 is somewhat far enough)

Let imagine a force pointing towards infinity away from source mass M, acting on this test mass m, the potential energy of m at this point would be therefore the work done by this external force.

WD= U_final-U_initial=U_r-U_∞

which means that the work done by external force is equal to the gravitational potential energy (U_r) since U_∞ = 0.

7.3.5 Suggested activity

The intent of these activities is to allow students be like a student-scientists and collect their own data to form an understanding of potential energy.

The test mass (green) is at r = 100 m, observe and record the value for U _r=100 = -6.67 x10^-11 J

Click play and pause the model when r = 90 m, record the value of U _r=90 = ____________ J

Click play and pause the model when r = 80 m, record the value of U _r=80 = ____________ J

Click play and pause the model when r = 70 m, record the value of U _r=70 = ____________ J

Click play and pause the model when r = 60 m, record the value of U _r=60 = ____________ J

Click play and pause the model when r = 50 m, record the value of U _r=50 = ____________ J

Click play and pause the model when r = 40 m, record the value of U _r=40 = ____________ J

Click play and pause the model when r = 30 m, record the value of U _r=30 = ____________ J

Click play and pause the model when r = 20 m, record the value of U _r=20 = ____________ J

Calculate the change in U from r = 100 to r = 50.

Answer is about $\mathrm{\Delta U}=-[\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(100\right)}{50}-\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(100\right)}{100}]=-6.67x10^{-9}J$

Check the "your model" checkbox and a teal color line appear. For example if the model is , $U=-\genfrac{}{}{0.1ex}{}{GmM}{r}$, key in -6.67*1*100/abs(r) and observe the closeness of fit of the orange color line (data collected) versus the teal color line (model proposed).

Suggest with reason why you think the model -6.67*1*100/abs(r) is accurate.

Note that the model already has a multiple of x10^-11 so there is no need to key it.

7.3.6 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/57

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity05/gravity05_Simulation.xhtml

 

Briefing Document: 🍎Gravitational Potential Energy Simulation Model

Date: October 26, 2024 Subject: Analysis of "7.3 Gravitational Potential Energy JavaScript HTML5 Applet Simulation Model" Source: Open Educational Resources / Open Source Physics @ Singapore Document URL: https://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity05/gravity05_Simulation.xhtml

1. Introduction

This document analyzes a web-based interactive simulation designed to help students understand gravitational potential energy (GPE). The simulation, built using Easy JavaScript Simulation (EJS), focuses on both the simplified (mgh) and more universal (-GMm/r) formulas for GPE, highlighting their applicability under different conditions. The resource aims to allow learners to gather data and explore GPE concepts like scientists.

2. Key Concepts and Themes

• Gravitational Potential Energy (GPE): The simulation explores the concept of gravitational potential energy, which is the energy an object possesses due to its position within a gravitational field.
• Two Formulas for GPE: The document presents and contrasts two key formulas for GPE:
• Simplified Formula (mgh or mgΔh): This formula is used when the gravitational field strength (g) is considered roughly constant, such as near the Earth's surface. As the text states, “the calculation of gravitational potential energy (GPE) is determined using the expression, mgh, which assumes that the gravitational field strength g is roughly constant.” The formula applies the change in height.
• Universal Formula (-GMm/r): This formula is more robust and accurate, especially when the gravitational field strength varies significantly, like when considering rockets traveling into space. The document notes, "a more robust formula is required for varying field strength, say when sending rockets which travel into outer space from the surface of the Earth."
• Reference Point: The document emphasizes the concept of a reference point for GPE. The simplified formula considers a reference height h0 while the universal formula uses infinity as its reference.
• "The gravitational potential energy (U) of a mass m at a point (due to the gravitational field set up by mass M ) is defined as the work done by an external agent in bringing the mass from infinity to that point r distance away from source mass M.”
• Work Done by External Agent: The document connects GPE to the work done by an external force in moving an object within the gravitational field, emphasizing that this work done by an external agent is equal to the potential energy (U).
• "WD= Ufinal-Uinitial=Ur-U∞ which means that the work done by external force is equal to the gravitational potential energy (Ur) since U∞ = 0."
• Negative GPE: The universal formula yields a negative value for potential energy as the simulation defines the potential to be zero at infinity. This negative sign reflects the attractive nature of gravity and indicates that the lowest potential is at the center of the source mass M, while zero is at infinity.
• "has only negative value due to the reference potential equal zero U = 0, position is defined at position r = infinity, ∞, and gravity is attractive which means the lowest potential position is at the centre of the source mass M."
• Scalar Quantity: It's noted that GPE is a scalar quantity, meaning it has magnitude but no direction.
• "a scalar quantity (i.e. it has no direction only magnitude )"
• Interactive Learning: The simulation encourages students to actively collect data and observe the relationship between distance and GPE by moving a test mass and observing the changing values for U, with suggested activities.
• Model Building: The user can check the "your model" box and propose a model to fit with the data collected. The students are also instructed to suggest with reason why you think the model -6.671100/abs(r) is accurate.

3. Key Formulas and Equations

• Simplified GPE: ΔU = ΔPE = mgh or mgΔh
• Where:
• ΔU or ΔPE is the change in gravitational potential energy.
• m is the mass of the object.
• g is the gravitational field strength (approximately 9.81 m/s² near Earth's surface).
• h or Δh is the change in height.
• Universal GPE: U = -GMm/r
• Where:
• U is the gravitational potential energy.
• G is the gravitational constant (approximately 6.673 × 10⁻¹¹ N⋅(m/kg)²).
• M is the source mass creating the gravitational field.
• m is the test mass experiencing the field
• r is the distance between the center of the source mass (M) and the test mass (m).
• Work Done by External Agent (and GPE): WD = U = ∫∞r F dr = -GMm/r. This is the mathematical explanation of the definition that GPE is the work done to bring the mass m from infinity to position r.

4. Simulation Activities and Examples

• The document includes a suggested activity for students to explore the simulation:
• Students are instructed to start the simulation, and record U at various distances (r),
• Students are then asked to calculate the change in U when the test mass moves from r=100 to r=50
• Students are also asked to propose their own model to fit with the data they collected.
• A suggested model is U = -6.67 * 1 * 100 / abs(r).
• The document also demonstrates sample calculations with given values for G, M, m and r:
• When r = 100 m, U = -6.67 x 10^-11 J
• When r = 50 m, U = -13.35 x 10^-11 J

5. Key Takeaways

• The simulation provides a visual and interactive way to explore GPE, its relation to work and its dependence on distance, especially in situations where the gravitational field strength is not constant.
• It helps students understand the limitations of the simplified mgh formula and the need for the more universal -GMm/r formula.
• The simulation encourages active learning by asking students to collect data, observe patterns, and connect the data with theoretical models.
• The activity allows students to have a "student-scientist" experience.

6. Additional Information

• The simulation is available as an embeddable model using iframe.
• The simulation is available as an app for Android devices.
• The webpage includes links to related physics topics as well as other simulations and tools.
• The webpage provides information about licensing and credits to the authors.

7. Conclusion

This interactive simulation is a valuable educational tool for teaching gravitational potential energy. It effectively demonstrates the concepts, formulas, and relationships involved, and it supports a hands-on approach to learning.

Gravitational Potential Energy Study Guide

Quiz

1. What is the standard formula for calculating gravitational potential energy (GPE) when assuming a constant gravitational field strength, and when is it appropriate to use? This is calculated using mgh, where m is the mass, g is the gravitational field strength (approximately 9.81 m/s² near the Earth's surface), and h is the height. It's appropriate when the gravitational field strength can be considered constant over the height difference.
2. Why is the formula U = -GMm/r considered more universal than mgh? The formula U = -GMm/r is more universal because it accounts for variations in gravitational field strength. This is necessary when the gravitational field strength is not constant, like when dealing with large changes in distance from a source mass, such as a rocket traveling far from Earth.
3. What do the variables represent in the formula U = -GMm/r? In the formula, U represents gravitational potential energy, G is the gravitational constant, M is the source mass creating the gravitational field, m is the test mass experiencing the field, and r is the distance between the center of mass M and the center of mass m.
4. Why is gravitational potential energy considered a scalar quantity? Gravitational potential energy is a scalar quantity because it only has a magnitude and no direction. It is a measure of the energy an object possesses due to its position in a gravitational field, not a vector quantity representing a force in a specific direction.
5. Why does gravitational potential energy have negative values, according to the provided source? Gravitational potential energy has negative values because the reference point where U=0 is defined at infinity. Since gravity is an attractive force, work must be done to move mass against the field to reach infinity. The lowest potential energy is at the center of mass M, as is represented by negative infinity.
6. How is gravitational potential energy defined in terms of work done by an external agent? Gravitational potential energy is defined as the work done by an external agent to move mass m from a point at infinity to a given distance r from source mass M against the gravitational force.
7. According to the source material, what happens to the potential energy as the test mass is moved closer to source mass M? As the test mass is moved closer to the source mass M, its potential energy decreases, becoming more negative. This is because work is done by the gravitational field on the mass as it moves closer.
8. In the simulation described, what does the test mass (green) represent? In the described simulation, the test mass (green) represents the mass m that is experiencing the gravitational field and whose gravitational potential energy is being evaluated.
9. What is the "your model" checkbox used for in the simulation activity, and what does the teal colored line represent? The "your model" checkbox is used to compare the user's proposed mathematical model for gravitational potential energy with the data collected from the simulation. The teal colored line represents the user's proposed model.
10. How does the described simulation help students understand gravitational potential energy? The simulation helps students understand gravitational potential energy by allowing them to collect and observe data points at various distances. This encourages students to become like student-scientists by actively working with the concept to form their own understanding of potential energy.

Quiz Answer Key

1. This is calculated using mgh, where m is the mass, g is the gravitational field strength (approximately 9.81 m/s² near the Earth's surface), and h is the height. It's appropriate when the gravitational field strength can be considered constant over the height difference.
2. The formula U = -GMm/r is more universal because it accounts for variations in gravitational field strength. This is necessary when the gravitational field strength is not constant, like when dealing with large changes in distance from a source mass, such as a rocket traveling far from Earth.
3. In the formula, U represents gravitational potential energy, G is the gravitational constant, M is the source mass creating the gravitational field, m is the test mass experiencing the field, and r is the distance between the center of mass M and the center of mass m.
4. Gravitational potential energy is a scalar quantity because it only has a magnitude and no direction. It is a measure of the energy an object possesses due to its position in a gravitational field, not a vector quantity representing a force in a specific direction.
5. Gravitational potential energy has negative values because the reference point where U=0 is defined at infinity. Since gravity is an attractive force, work must be done to move mass against the field to reach infinity. The lowest potential energy is at the center of mass M, as is represented by negative infinity.
6. Gravitational potential energy is defined as the work done by an external agent to move mass m from a point at infinity to a given distance r from source mass M against the gravitational force.
7. As the test mass is moved closer to the source mass M, its potential energy decreases, becoming more negative. This is because work is done by the gravitational field on the mass as it moves closer.
8. In the described simulation, the test mass (green) represents the mass m that is experiencing the gravitational field and whose gravitational potential energy is being evaluated.
9. The "your model" checkbox is used to compare the user's proposed mathematical model for gravitational potential energy with the data collected from the simulation. The teal colored line represents the user's proposed model.
10. The simulation helps students understand gravitational potential energy by allowing them to collect and observe data points at various distances. This encourages students to become like student-scientists by actively working with the concept to form their own understanding of potential energy.

Essay Questions

1. Compare and contrast the calculation of gravitational potential energy using mgh and U = -GMm/r. Discuss the scenarios where each formula is appropriate and explain why using the wrong formula might lead to inaccurate results.
2. Explain the concept of defining gravitational potential energy in terms of work done by an external agent. Discuss the importance of setting the reference point at infinity and why this leads to negative values for gravitational potential energy near a source mass.
3. Describe the experimental approach suggested in the provided simulation activity and how this model helps students develop a deeper understanding of gravitational potential energy, considering that it is a scalar with only negative values.
4. Evaluate how the simulation aids in the understanding of the relationship between distance and gravitational potential energy. Discuss how the "your model" feature allows students to test their theoretical understanding against experimental data.
5. Discuss the concept of gravitational potential energy and how it relates to general energy conservation principles. Explain how gravitational potential energy can be transformed into other forms of energy, such as kinetic energy.

Glossary of Key Terms

• Gravitational Potential Energy (GPE): The energy an object possesses due to its position in a gravitational field. It is a scalar quantity, measured in Joules (J).
• mgh: The formula for calculating GPE assuming a constant gravitational field strength (g), where m is mass and h is height.
• U = -GMm/r: The formula for calculating GPE that accounts for varying gravitational field strength, where G is the gravitational constant, M is the source mass, m is the test mass, and r is the distance between them.
• Scalar Quantity: A quantity that has magnitude only and no direction. GPE is a scalar quantity.
• Gravitational Constant (G): A fundamental constant in physics, approximately 6.673 × 10⁻¹¹ N(m/kg)².
• Source Mass (M): The mass that creates a gravitational field around it.
• Test Mass (m): The mass experiencing the gravitational field created by the source mass.
• Reference Point: The point where the gravitational potential energy is defined as zero, typically at an infinite distance from the source mass.
• Work Done by an External Agent: The amount of energy transferred when a force is applied to move an object against a gravitational field.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.gravity05app896563&hl=en

Video

https://notebooklm.google.com/notebook/133441be-c731-461e-8c88-11b10d6fdba1/audio

Timeline of Main Events

• Conceptual Introduction of Gravitational Potential Energy: The document begins by introducing the concept of gravitational potential energy (GPE), initially using the simplified formula mgh, which assumes a constant gravitational field.
• Need for a More Robust Formula: It's explained that the simple mgh formula is inadequate for scenarios where the gravitational field strength varies significantly, such as with rockets traveling far from Earth.
• Introduction of the Universal Formula: The more universal formula for GPE is introduced: U = -GmM/r. This formula takes into account varying field strength.
• Explanation of Terms: The components of the formula are defined, including U (gravitational potential energy), G (gravitational constant), M (source mass), m (test mass), and r (distance from the source mass).
• Negative Value of GPE: The document highlights that GPE is a scalar quantity with only negative values, with the reference point of zero potential at infinity.
• Definition of GPE: GPE is formally defined as the work done by an external agent to bring a mass from infinity to a point a distance 'r' from the source mass.
• Mathematical Derivation The work done equation is shown to be equivalent to the Gravitational Potential Energy equation via calculus.
• Simulation Based Learning: The document suggests using a simulation to help learners understand this definition, suggesting recording values of U at different values of r within the simulation.
• Activity for Students: A series of activities are suggested for students, having them observe and record changes in potential energy values as the test mass moves closer to the source mass within the simulation.
• Model Verification: Students are asked to verify that the model -6.671100/abs(r) is accurate.
• Use of the Simulation Users are directed to the simulation for use.
• Availability of Resources: The document provides links to access the simulation online and through a mobile app.
• Credit Acknowledgements: Credits are provided to the creators of the simulation and the related open source physics tools.

Cast of Characters

• Anne Cox: Contributed to the development or creation of the open educational resources.
• Wolfgang Christian: A contributor to the open educational resources, likely involved in the development of the simulation or its physics content.
• Francisco Esquembre: A contributor to the open educational resources, likely involved in the development of the simulation or its underlying code.
• Loo Kang WEE (lookang): User who has uploaded and created the content. 

Frequently Asked Questions About Gravitational Potential Energy

1. What is gravitational potential energy (GPE), and how is it typically calculated in introductory physics?
2. Gravitational potential energy (GPE), often symbolized as U or PE, represents the energy an object possesses due to its position within a gravitational field. In introductory physics, when we assume the gravitational field strength (g) is constant, the GPE is calculated using the formula mgh or mgΔh. Here, 'm' is the mass of the object, 'g' is the acceleration due to gravity (approximately 9.81 m/s² on Earth), and 'h' or 'Δh' is the object's height (or change in height) relative to a reference point.
3. Why is the simple mgh formula not always sufficient for calculating gravitational potential energy?
4. The formula mgh assumes that the gravitational field strength 'g' remains constant, which is a reasonable approximation when dealing with objects near the Earth's surface. However, when considering situations like rockets traveling into space, where the distance from the Earth's center significantly changes, the gravitational field strength varies considerably. Therefore, a more universal and robust formula is required.
5. What is the more universal formula for gravitational potential energy, and how does it differ from the simple mgh formula?
6. The more universal formula for gravitational potential energy is given by: U = -GmM/r, where:

• U is the gravitational potential energy.
• G is the gravitational constant (approximately 6.673 × 10⁻¹¹ N·(m/kg)²).
• M is the mass of the source creating the gravitational field (e.g., Earth).
• m is the mass of the object experiencing the field.
• r is the distance between the center of the source mass M and the object m. This formula accounts for the changing gravitational field strength as the distance from the source mass varies, making it more accurate for larger distances and for objects not near the surface of a planet. It's important to note that unlike mgh, where you pick a zero point of potential energy, the U = -GmM/r equation sets gravitational potential to zero when r is infinite.

1. Why is gravitational potential energy always negative in the universal formula?
2. In the universal formula (U = -GmM/r), gravitational potential energy is always negative because we define the zero potential energy point as being infinitely far away from the source mass (r = ∞). Since gravity is an attractive force, as an object is brought closer to the source of gravity, work is done by gravity and the potential energy is converted to kinetic energy, reducing the initial energy. Therefore, the potential energy decreases from zero to a negative value as r decreases. The closer an object gets to the source of gravity (as r gets smaller), the more negative the gravitational potential energy becomes, with its lowest possible potential being at the center of the source mass M (when r=0)
3. How is gravitational potential energy defined in terms of work done by an external agent?
4. Gravitational potential energy is defined as the work done by an external agent to move an object from an infinite distance away to a distance r from the source mass against the gravitational force. This work is equivalent to the gravitational potential energy of the object at that point. Because gravitational force is attractive, external work is required to pull an object away from a source of gravity, which results in the potential energy increasing to zero at infinity. The equation given by this definition matches the negative of the universal potential energy equation. This work definition also accounts for the negative value of potential energy in the U = -GmM/r equation as the work done by gravity is the opposite of the work done by the external agent.
5. What are some key characteristics of gravitational potential energy as defined by the universal formula?

• Scalar Quantity: Gravitational potential energy is a scalar quantity, meaning it has magnitude but no direction.
• Negative Value: The universal formula results in a negative value, which stems from the definition that potential energy is zero at infinity.
• Reference Point: The reference position for zero potential energy is defined at an infinite distance away from the source mass. The potential energy becomes increasingly negative as the object moves closer to the source.
• Lowest at Center: The gravitational potential energy is lowest (negative infinity) at the center of the source mass.

1. How can the provided simulation model be used to understand gravitational potential energy?
2. The provided simulation can be used to visualize the concept of gravitational potential energy, with a test mass shown as a green circle moving towards a gravitational source. You can interact with the simulation to record potential energy values at various distances (r) from the source mass. By recording and calculating changes in U at different distances, students can gain an understanding of how potential energy changes with distance. Additionally, students can test the proposed model U = -GmM/r against the data gathered from the model using the provided checkbox feature.
3. What are the intended activities for students using this simulation model and what key concept should they learn?
4. The suggested activities are designed for students to act as scientists. They are encouraged to gather their own data of GPE at different distances from a source mass. By doing so, they can formulate a deeper understanding of how potential energy changes as objects are moved in the gravitational field, and confirm the accuracy of the universal equation for gravitational potential energy. The main focus is to move students from a superficial understanding of the equation, to an understanding of the physics behind gravitational potential energy.