About

7.1.5 Example (N09/I/16) Binary Stars 

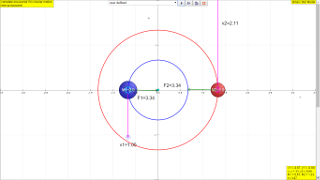
Two stars of mass M and 2M, at a distance 3x apart, rotate in circles about their common centre of mass O.
The gravitational force acting on the stars can be written as $\genfrac{}{}{0.1ex}{}{kG{M}^2}{x^2}$ .
What is the value of k?
A  0.22             B  0.50                C  0.67             D  2.0

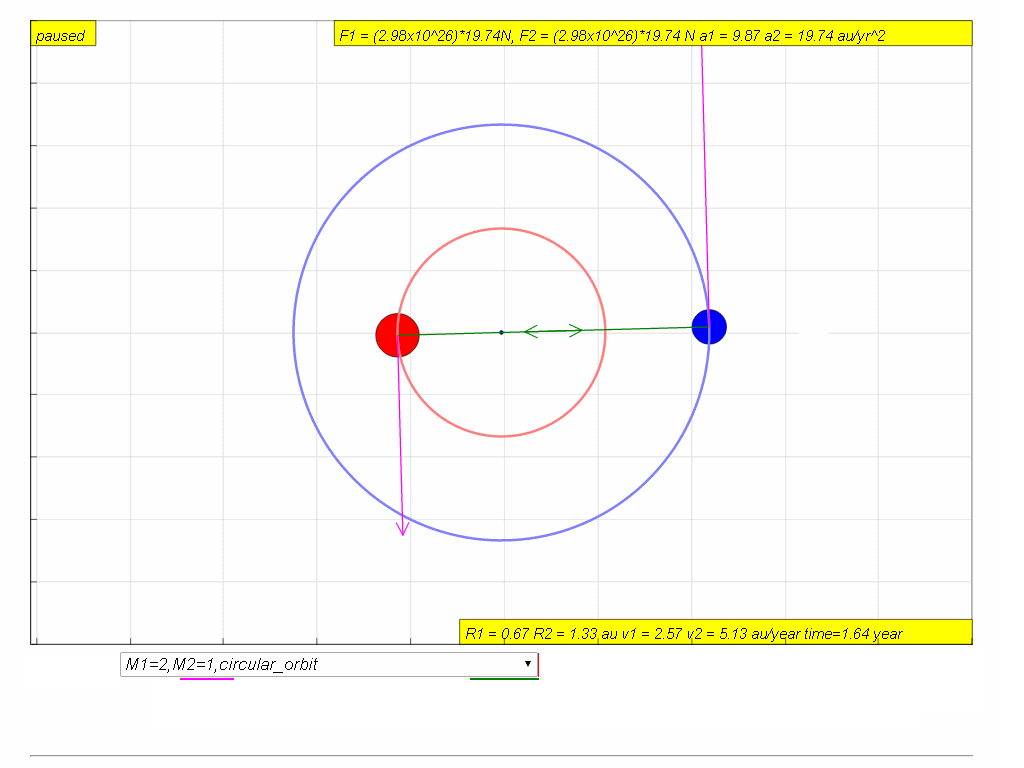
7.1.5.1 Model: You may view the movement of the two stars using the EJSS below link (require internet) or just below:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/53

Answer is $\left|F\right|=G\genfrac{}{}{0.1ex}{}{M_1{M}_2}{r^2}=G\genfrac{}{}{0.1ex}{}{2MM}{{\left(3x\right)}^2}=\genfrac{}{}{0.1ex}{}{2}{9}G\genfrac{}{}{0.1ex}{}{M^2}{{\left(x\right)}^2}$

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang - Dept. of Physics,National Taiwan normal Univ.; Loo Kang Wee; Wolfgang Christian

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity02_1/gravity02_1_Simulation.xhtml

 

Briefing Document: 💫Binary Star Simulation & Educational Resources

Subject: Review of "7.1.5 (N09/I/16) Binary StarsJavaScript HTML5 Applet Simulation Model" and related Open Educational Resources.

Date: October 29, 2024

1. Overview:

This document analyzes a webpage focused on a JavaScript HTML5 applet simulation model for binary stars. It is hosted on Open Educational Resources / Open Source Physics @ Singapore. This source is part of a broader collection of interactive simulations and educational resources, primarily for physics, but also touching on math, chemistry and other fields. The document will outline the specifics of the binary star model, and also the context of the project within the larger collection of resources.

2. Key Themes and Concepts

• Interactive Simulation for Learning: The core of this resource is an interactive simulation of a binary star system. This approach aligns with the trend of using technology to improve learning by providing hands-on experience rather than passive lectures or reading.
• Binary Stars as a Physics Problem: The simulation is framed by a specific physics question involving two stars with masses M and 2M, separated by a distance of 3x, rotating about their common center of mass. The core problem revolves around calculating the value of k in the gravitational force equation. The given answer uses a calculation of the general form of:
• | F | = G M 1 M 2 r 2 = G 2 M M ( 3 x ) 2 = 2 9 G M 2 ( x ) 2
• Open Educational Resources (OER): The source material is part of a larger OER initiative aiming to provide freely available, accessible educational tools. The site openly encourages embedding of the models in other webpages, emphasizing its open nature.
• "Embed this model in a webpage:
• "
• Accessibility Across Platforms: The models, built with Easy JavaScript Simulations (EJS), are designed to function across various platforms (Windows, MacOS, Linux, Chromebooks, Android/iOS), making them accessible on a wide range of devices. "Android/iOS including handphones/Tablets/iPads" "Windows/MacOSX/Linux including Laptops/Desktops" "ChromeBook Laptops"
• Focus on Inquiry-Based Learning: Many of the simulation tools, including the binary star one, are designed to allow students to investigate scientific concepts themselves, rather than simply receiving answers.
• Collaboration & Attribution: The projects are attributed to several authors, highlighting collaborative work in developing these materials. Credits for the binary star simulation are given to "Fu-Kwun Hwang - Dept. of Physics,National Taiwan normal Univ.; Loo Kang Wee; Wolfgang Christian".
• Emphasis on Interactive and Visual Learning: Many resources mentioned use JavaScript simulations and HTML5 to create highly visual, interactive experiences, making complex scientific concepts more accessible.

3. Key Facts and Ideas

• Binary Star Simulation Details:
• Two stars with masses M and 2M.
• Initial distance of 3x between the stars.
• Stars rotate in circles about their center of mass.
• The gravitational force is stated as: k G M 2 / x 2
• The answer and working is provided as:
• | F | = G M 1 M 2 r 2 = G 2 M M ( 3 x ) 2 = 2 9 G M 2 ( x ) 2
• Easy JavaScript Simulations (EJS): This is a software used to develop the simulations. A link is included to the EJS License which is necessary for "commercial use of EasyJavaScriptSimulations Library".
• Variety of Simulation Topics: The page showcases an extensive range of simulations beyond just binary stars, including topics such as:
• Energy and Motion (Pendulums, collisions, projectile motion)
• Waves and Optics (Diffraction, interference)
• Electricity and Magnetism (Electromagnetism, capacitors)
• Thermodynamics (Heat transfer, rates of reaction)
• Mathematics (Geometry, trigonometry)
• And several others.
• Examples of listed simulation titles: "Energy Pendulum Model for Primary", "Newton Cradle (3D) JavaScript HTML5 Applet Simulation Model", "Projectile Motion Energy Model", "Oscilloscope Model JavaScript HTML5 Applet Simulation Model", "Earth and Bar Magnet JavaScript HTML5 Applet Simulation Model", and many, many more.
• Links to Additional Resources: The page links to the PhET Interactive Simulations website from the University of Colorado, indicating a network of available resources.

4. Implications and Potential Uses

• Enhanced Physics Education: The simulations offer an engaging and interactive method for teaching complex physics concepts. The binary star simulation, in particular, allows students to experiment with the relationship between mass, distance, and gravitational force.
• Support for Teachers: These free, ready-made simulations could save teachers time in creating learning materials. The resources are already developed and can be implemented in a number of classroom settings.
• Improved Student Engagement: The interactive nature of simulations helps boost student engagement, especially for students who may learn better visually and with active interaction.
• Broader Applications: The range of simulations offered across different subjects makes the OER collection a valuable resource for teachers of physics, mathematics, chemistry and other subjects.

5. Conclusion

The "7.1.5 (N09/I/16) Binary StarsJavaScript HTML5 Applet Simulation Model" is a specific example of the high-quality, open-source, interactive educational resources available on this website. These resources are a powerful tool for engaging students in scientific and mathematical learning. The use of EJS for cross-platform compatibility, the emphasis on open access, and the wide variety of simulation topics make this resource a valuable contribution to online education.

 

Binary Stars Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What are binary stars?
2. In the context of the provided resource, how are the masses of the two stars related?
3. What is the significance of the "common center of mass O" in this system?
4. According to the text, what is the distance between the two stars?
5. The gravitational force is written as a constant (k) multiplied by the formula given in the resource; what is that formula?
6. What is the numerical value for "k" in the example provided?
7. What does the simulation allow you to visualize in regards to the two stars?
8. What does the resource identify as the full formula for gravitational force?
9. What is the relationship between the distance between the two stars (r) and the separation distance used in the problem?
10. List three other simulation topics/models that are found on the site.

Quiz Answer Key

1. Binary stars are systems consisting of two stars that are gravitationally bound and orbit around a common center of mass. They are not just two stars that are near each other; they are in orbit around one another.
2. In this specific example, the masses are related by a factor of two, where one star has a mass of M and the other has a mass of 2M. This means the more massive star is twice the mass of the less massive star.
3. The common center of mass (O) is the point around which both stars orbit. It is the balance point of the system and is not necessarily located halfway between the two stars when their masses differ.
4. According to the text, the distance between the two stars is 3x, where x is an arbitrary unit of distance. This means that there is a fixed distance of 3x between the two stars at all times.
5. The formula is G * M * 2 / x^2. This is the formula for the gravitational force between the two stars using the values given in the question and its example.
6. The numerical value for "k" is stated in the resource as 2/9, which as a decimal is approximately 0.22.
7. The simulation allows you to visualize the movement of the two stars as they orbit around their common center of mass, and you may observe how the stars' orbital paths change.
8. The full formula for gravitational force is | F | = G * M1 * M2 / r^2, where G is the gravitational constant, M1 and M2 are the masses of the two objects, and r is the distance between their centers.
9. The distance "r" in the gravitational force formula corresponds to 3x in the example provided; this means the variable "r" in the formula is equal to "3x" in the model.
10. Three other topics include "Moon Phases with Sea Tides," "Energy Pendulum Model," and "Ferris Vertical Circular Wheel."

Essay Questions

Instructions: Answer the following essay questions thoroughly. Support your claims with evidence from the source material and a well-organized response.

1. Explain the relationship between the masses of the stars, their distance apart, and the force of gravity that governs their interaction, and explain how the center of mass affects the system's motion.
2. Discuss the significance of the simulation as a tool for understanding the dynamics of binary star systems. What are its advantages and limitations for learning about celestial mechanics?
3. Describe the process used to derive the value of "k," given the provided information and equations, and how this demonstrates an understanding of the force of gravity between two objects.
4. How does the provided example demonstrate the application of Newton's Law of Universal Gravitation?
5. Considering the wide range of simulations and topics covered on the website, discuss how these models can be used in education to make various scientific and mathematical topics more accessible and engaging.

Glossary of Key Terms

• Binary Star: A system of two stars that are gravitationally bound to each other and orbit around a common center of mass.
• Gravitational Force: The attractive force that exists between any two objects with mass.
• Center of Mass: The point around which the total mass of a system is evenly distributed; in a binary system, this is the point around which both stars orbit.
• G (Gravitational Constant): The proportionality constant in Newton's law of universal gravitation; it is a fundamental constant of physics.
• M (Mass): A measure of the amount of matter in an object, a property of matter that determines its gravitational force.
• r (Distance): The separation between the centers of two objects in space; in this context, this the distance between the two stars.
• Simulation Model: A virtual representation of a system or phenomenon used to study its behavior, such as the example of orbiting stars.
• EJSS: An abbreviation for Easy JavaScript Simulations, which is a tool used to create interactive simulations.
• Orbit: The curved path of a celestial object around a star, planet, or moon; in a binary system, each star orbits the center of mass of the system.

 App

• gravity02_1.apk

Video

https://notebooklm.google.com/notebook/b4cec6c8-2a72-429b-8865-82bd29bc4320/audio

Versions

1. http://weelookang.blogspot.sg/2016/07/binary-stars-javascript-model-by-fu.html

Other resources

1. https://phet.colorado.edu/sims/my-solar-system/my-solar-system_en.html

 

Timeline of Main Events and Concepts

• Undated (Conceptual): The concept of binary stars is introduced, described as two stars (one with mass M, the other with mass 2M) orbiting a common center of mass. Their separation is defined as 3x. The gravitational force acting between them is discussed and calculated.
• Undated (Conceptual/Model): The simulation model gravity02_1 is developed, a Javascript HTML5 Applet Simulation model created to visualize the movement of binary stars. This model can be embedded in webpages.
• Undated (Ongoing): Various educational resources, simulations, and interactive tools are developed using Easy JavaScript Simulation (EJS) and WebEJS platforms. These cover a wide range of topics across physics, mathematics, chemistry, and other disciplines, often designed for primary and secondary school levels.
• 2016/07: The blog post about the binary stars JavaScript model by Fu-Kwun Hwang appears. This is the earliest publication date we have for the binary star model.
• 2019-2024: A period of intense activity and development around EJS and WebEJS, resulting in numerous workshops, presentations, and projects focused on using these tools for creating interactive educational content. This includes both teacher training and student engagement.
• 2019-2024 (ongoing): Numerous new educational resources, simulations, and interactive tools are developed, encompassing a range of subjects beyond binary stars. These include topics like:
• Mechanics (e.g. projectile motion, collisions, pendulums, vector addition, free fall)
• Electromagnetism (e.g. magnetic fields, induction)
• Optics (e.g. diffraction, interference, resolution)
• Thermodynamics (e.g. rates of reaction)
• Math (e.g. geometry, coordinates, games, telling time)
• Chemistry (e.g. electrolysis, ionic bonding, molecular models)
• Geography and other subjects.
• New simulations for learning tools using Javascript, HTML5, and EJS/WebEJS.
• Various Dates (2021-2024): Specific workshops and events focusing on the use of EJS/WebEJS for education, including:
• Teacher training workshops (e.g., 20230327, 20240718-24)
• Presentations and sharing sessions on the use of interactive simulations in teaching (e.g., 20230302, 20230511)
• Project team meetings (e.g., 20230727)
• Dialogue sessions on Math apps and customisable apps (e.g., 20230802)
• Brown bag sessions (e.g., 20230728, 20240815)
• Conferences such as MPTL26 (20230907-09)
• 2024 Ongoing: Development and application of these tools continue, with a focus on accessibility, customization, and integration with platforms like the Student Learning Space (SLS).

Cast of Characters

• Fu-Kwun Hwang: A professor in the Department of Physics at the National Taiwan Normal University. He is a key figure in the development of educational simulations using EJS and is credited with the creation of the binary stars JavaScript model.
• Loo Kang Wee aka lookang: A collaborator in the project, based in Singapore, and heavily involved in the creation and promotion of Open Source Physics educational resources. Also involved in workshops, presentations, and dialogues. The administrator of the website and the main user of the account
• Wolfgang Christian: Another collaborator in the project, co-creator of the 3D Wave Machine JavaScript Model.
• Francisco Esquembre: Contributed to the Web EJS beta Workshop
• Félix J. García Clemente: Contributed to the Web EJS beta Workshop
• Douglas Brown: Developed the Tracker Toss Out Projectile Model.

Key Themes and Observations

• Open Educational Resources: The project emphasizes the use of open-source tools and resources, making simulations accessible to educators and learners.
• Interactive Learning: The focus is on creating interactive simulations that actively engage students and facilitate a deeper understanding of concepts.
• EJS/WebEJS as a Core Tool: The Easy JavaScript Simulation toolkit and its web-based counterpart WebEJS are central to the creation of these resources.
• Collaboration and Community: The development process involves a community of educators, researchers, and developers, fostering collaborative learning and resource sharing.
• Multidisciplinary Approach: The scope of simulations covers a wide range of subjects, demonstrating the versatility of the tools.
• Continuous Development: The project is an ongoing effort, with continuous updates, new simulations, and workshops being developed and added over time.

FAQ: Binary Star Systems and Interactive Physics Simulations

• What is a binary star system, and how does it relate to the simulation mentioned in the source? A binary star system consists of two stars orbiting around a common center of mass due to their mutual gravitational attraction. The simulation in the source, specifically the "7.1.5 (N09/I/16) Binary Stars JavaScript HTML5 Applet Simulation Model," allows users to visualize the motion of two stars of different masses (M and 2M) orbiting their center of mass, demonstrating the principles of gravitational forces and orbital mechanics.
• What is the main physics concept demonstrated in the binary star simulation? The simulation primarily demonstrates the gravitational force between two masses and how it causes them to orbit around their common center of mass. It also illustrates how the masses and separation distance of the stars influence the gravitational force and their respective orbital paths. Furthermore, it implicitly shows Newton's Law of Universal Gravitation and can be used to determine the constant k within the provided equation relating force to mass and distance.
• How is the gravitational force between the two stars calculated in the simulation's model? The gravitational force between two stars is calculated based on Newton's Law of Universal Gravitation, which is expressed as |F| = G * M1 * M2 / r^2, where F is the gravitational force, G is the gravitational constant, M1 and M2 are the masses of the two stars, and r is the distance between their centers. In the specific binary star example provided, the equation is given as |F| = G * 2M * M / (3x)^2 = 2/9 * G * M^2 / x^2. This example calculates the gravitational force when one star has mass M, the other has mass 2M, and their distance is 3x, highlighting how the total separation distance affects the gravitational interaction. This also solves for the constant k as 2/9.
• What is Easy JavaScript Simulation (EJS), and how is it used in the context of these interactive resources? Easy JavaScript Simulation (EJS) is an open-source tool used to create interactive simulations, often focusing on physics concepts. EJS is used to develop and embed these models into webpages, making them accessible across different platforms (desktops, laptops, tablets, smartphones) using HTML5. These interactive simulations facilitate learning by allowing users to visualize and manipulate physical parameters. The source mentions webEJS as a modern platform for interactive simulations, suggesting an evolution or variation on EJS.
• What other types of interactive simulations are available within this resource besides the binary star model? This resource offers a wide range of interactive simulations, not just limited to gravitational mechanics. The list includes models for topics like simple harmonic motion (Energy Pendulum, Ferris Wheel, Newton's Cradle), collisions (Collision Carts), projectile motion, electromagnetism (Earth and Bar Magnet, 2 Magnetic Bars, Magnet Falling in a Coil, Electromagnet Strength), optics (Michelson Interferometer, Double Slit Diffraction), thermodynamics, and even chemistry and math concepts (Rates of Reactions, Electrolysis, Multiple Slit Diffraction, Digital Time). There are also simulations for areas outside STEM such as games and quizzes that support literacy and digital literacy.
• How can teachers or educators use these simulations in a classroom or learning environment? Teachers and educators can integrate these simulations to enhance student engagement by providing visual and interactive representations of abstract concepts. These simulations can be used for demonstrations, exploration, and even as part of assignments. They can use the models to let students see the effects of parameter changes first hand. For example, adjusting the masses of the binary stars and observing the resulting effect can improve conceptual understanding in physics. The resource itself describes ways educators can learn to use the tools to make their own simulations and also provides examples on how this is being incorporated into the Student Learning Space (SLS), a national educational platform. There is an emphasis on using these simulation to support literacy and numerical literacy using different interactive formats.
• Are these simulations accessible on various devices and platforms? Yes, these simulations are designed to be accessible across multiple platforms and devices, including Windows, MacOSX, Linux, Chromebook laptops, and Android/iOS devices (including handphones/tablets/iPads). They are designed using HTML5, ensuring broad compatibility. This means that they can be easily integrated into web-based learning environments and can be used regardless of the type of computer or mobile device that a student or teacher is using.
• Is the use of these interactive simulations free and open for educational purposes? The source indicates that the content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License, meaning that it is free to use, share, and adapt for non-commercial purposes with proper attribution. However, for commercial use of the EasyJavaScriptSimulations library, there may be a different license and the user must directly contact This email address is being protected from spambots. You need JavaScript enabled to view it. and read the linked license.