About

7.2 Gravitational Field Strength (symbol: g and units: N kg^-1 or m s^-2)

As seen in earlier section, the gravitational field strength acting at a point in the field (previously depicted as M₂ = 1kg) decreases (illustrated by an increase in the field line spacing) as the point moves further away from Earth. This means that field strength varies with distance from the source mass (in this case, the Earth).

The gravitational field strength, g at a particular point in free space is defined as the gravitational force per unit mass acting on a point mass placed at that point.

7.2.1 Why point mass assumption:

Why must it be a 'point mass'?
To simplify analysis, point mass are used as they are physically very small so that the point mass itself does not distort the gravity field of its surrounding. Another reason could be that the forces acting on different parts of the point mass are generally the same.

7.2.2 g LO(C)

7.2.2.1 Equation

Based on Newton’s law of gravitation, the gravitational force acting on the point mass, m by the source mass, M, (notice M₁ is denoted by M and M₂ is denoted by m respectively)$$

$F=\frac{G{M}_1{M}_2}{r^2}$   

$F=\genfrac{}{}{0.1ex}{}{GMm}{r^2}$ ---------------------------------------------------------- (1)

and gravitational field strength, g is the gravitational force, F per unit mass acting on the point mass, m, we may derive the gravitational field strength.

Since we know the force on object as a result of the gravitational field created by Earth is 

F = mg  --------------------------------------------------------- (2)

putting the equations (1) and (2) together, we get  
$$    

$F=mg=m\genfrac{}{}{0.1ex}{}{GM}{r^2}$

giving us the expression for gravitational field field g

$g=\genfrac{}{}{0.1ex}{}{GM}{r^2}$

7.2.2.2 Graphical representation

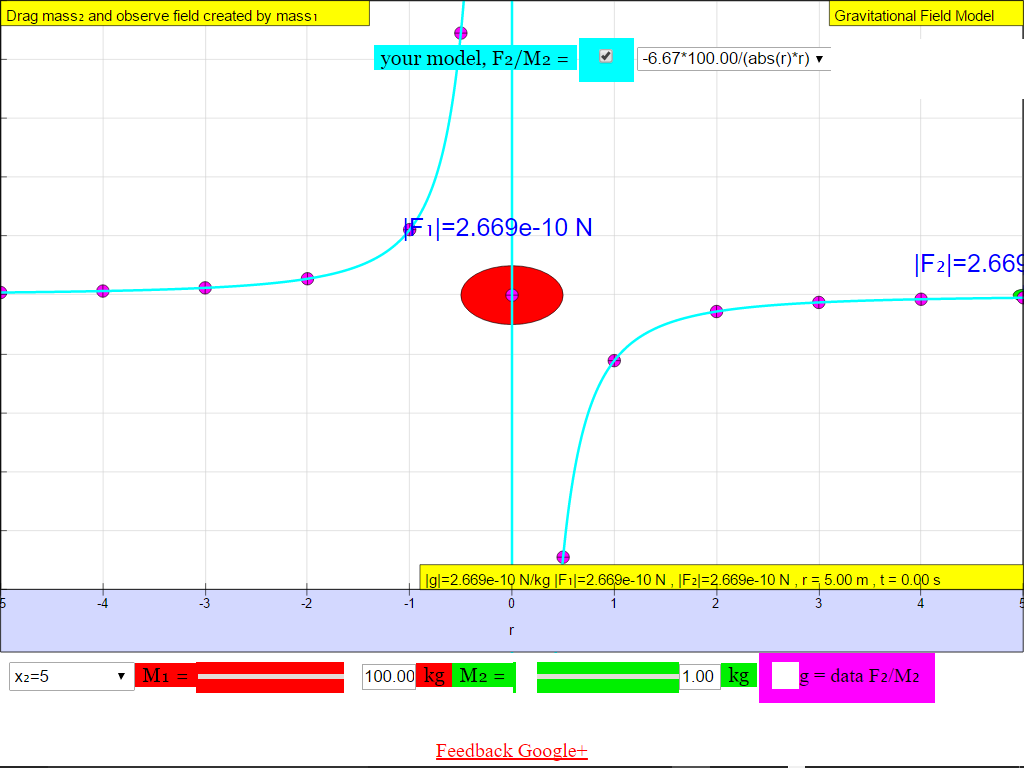
The following shows the different g field strength at different positions away from the mass M creating the gravitational field.
From left to right, for the case when M = 100 kg.

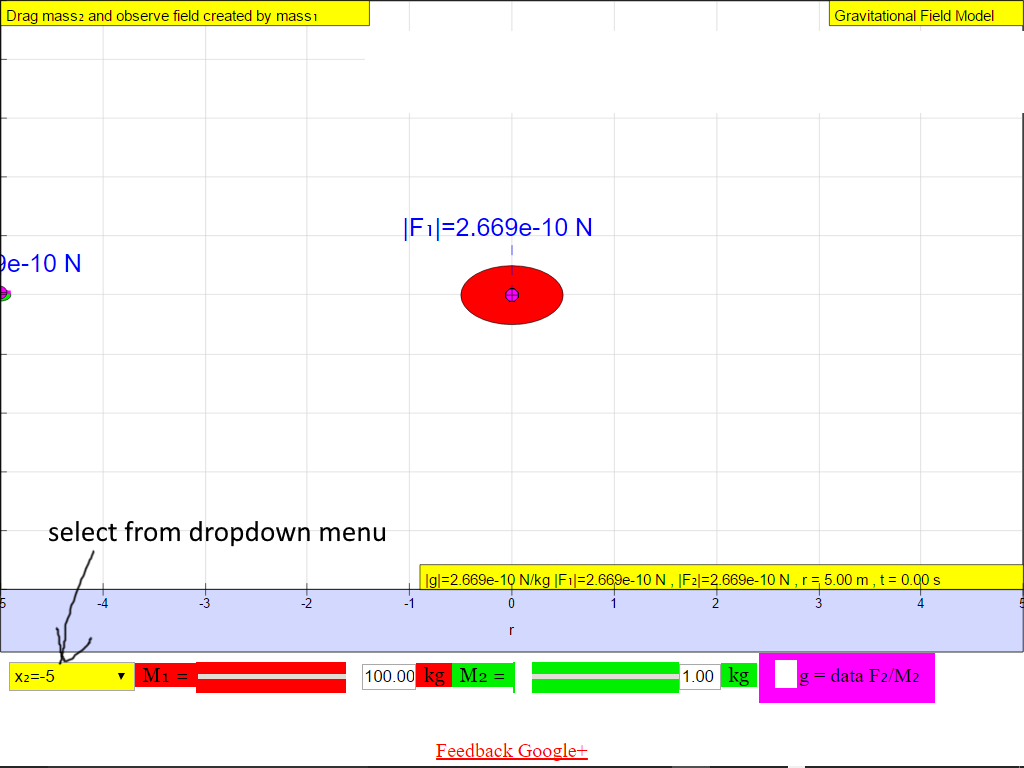
When r = -5.0 m, |g| = 2.669x10^-10 N/kg towards M

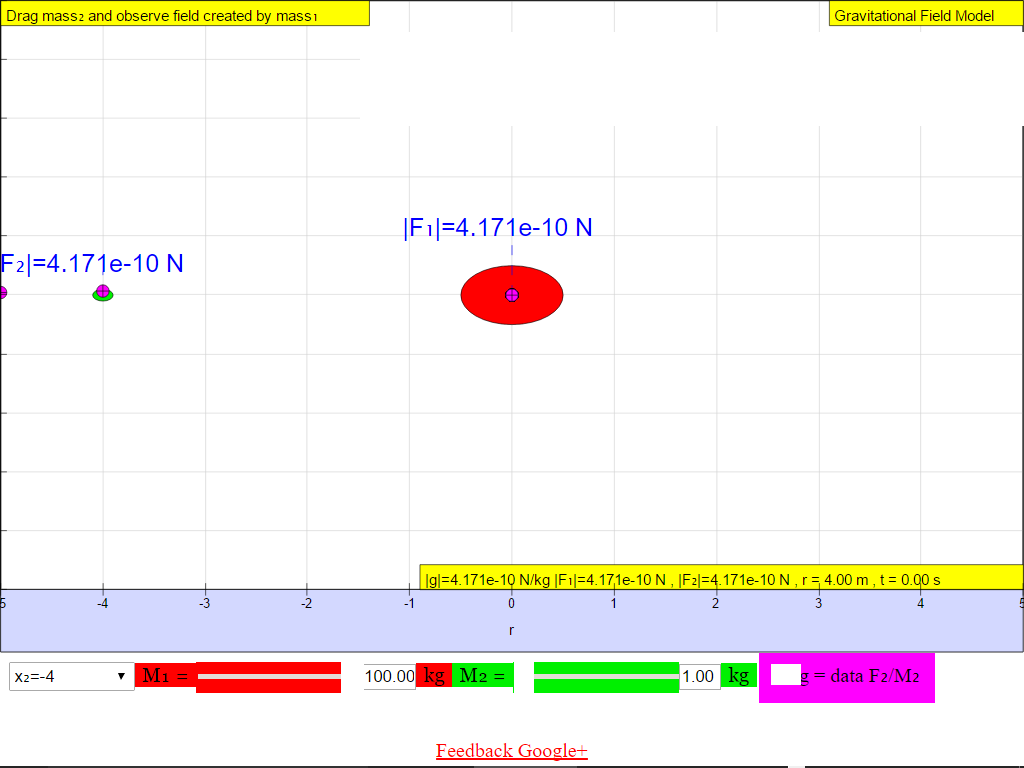
When r = -4.0 m, |g| = 4.171x10^-10 N/kg towards M

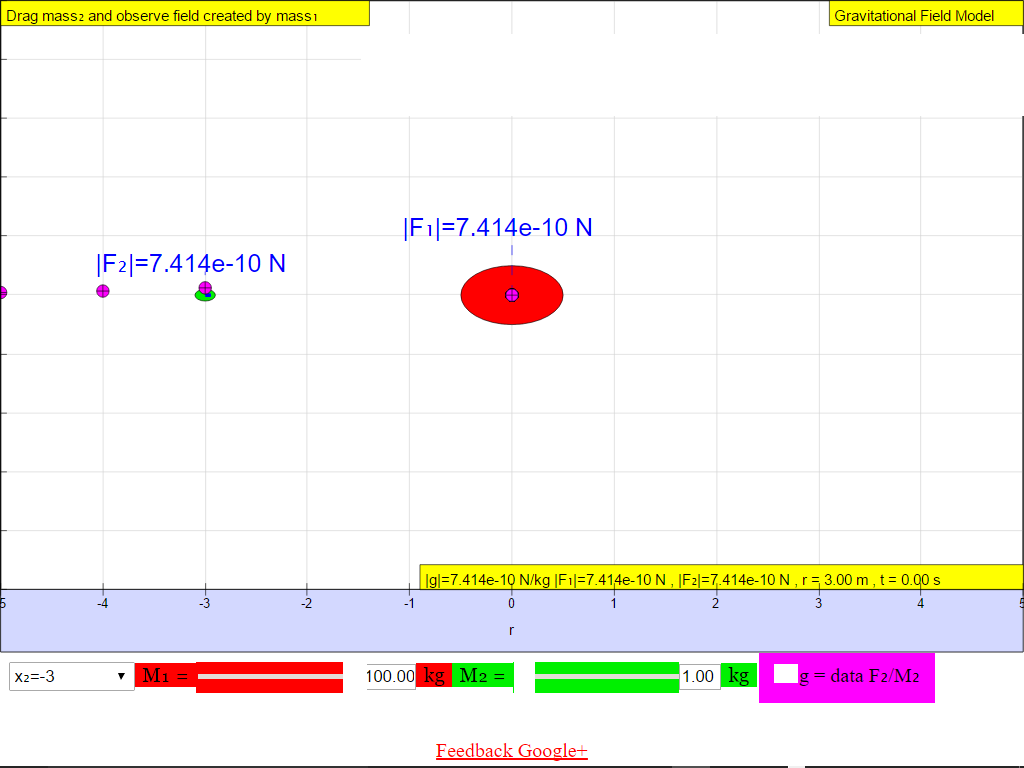
When r = -3.0 m, |g| = 7.414x10^-10 N/kg towards M

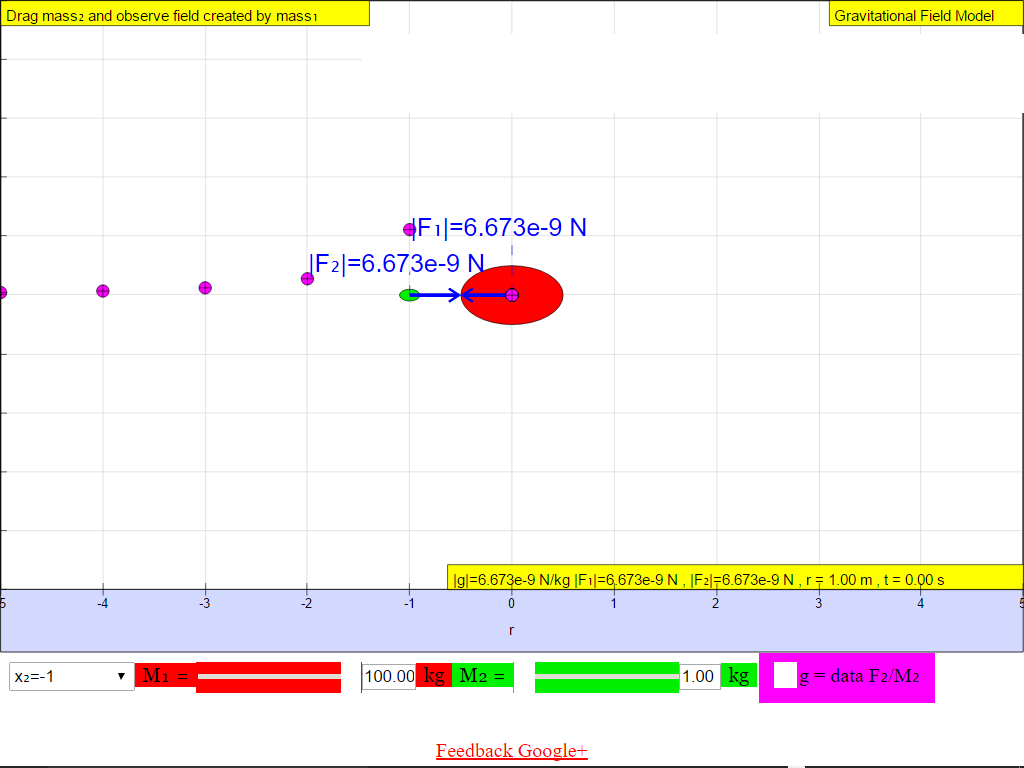
When r = -2.0 m, |g| = 1.672x10^-10 N/kg towards M

When r = -1.0 m, |g| = 6.673x10^-9 N/kg towards M






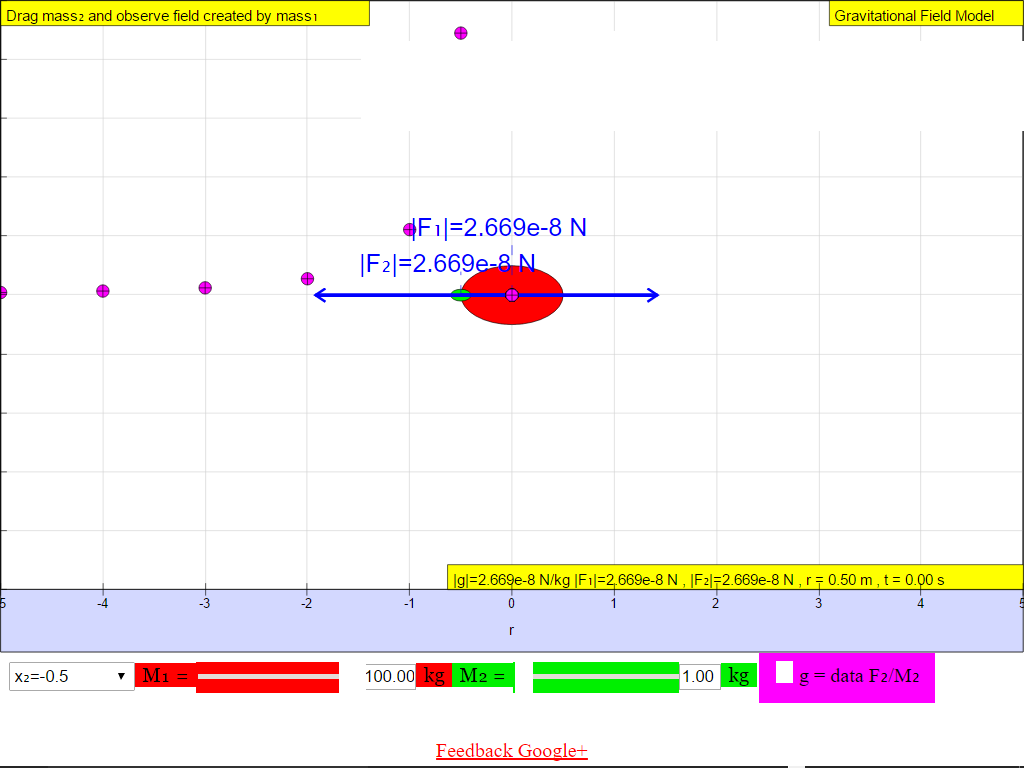
When r = -0.5 m, |g| = 2.669x10^-8 N/kg towards M




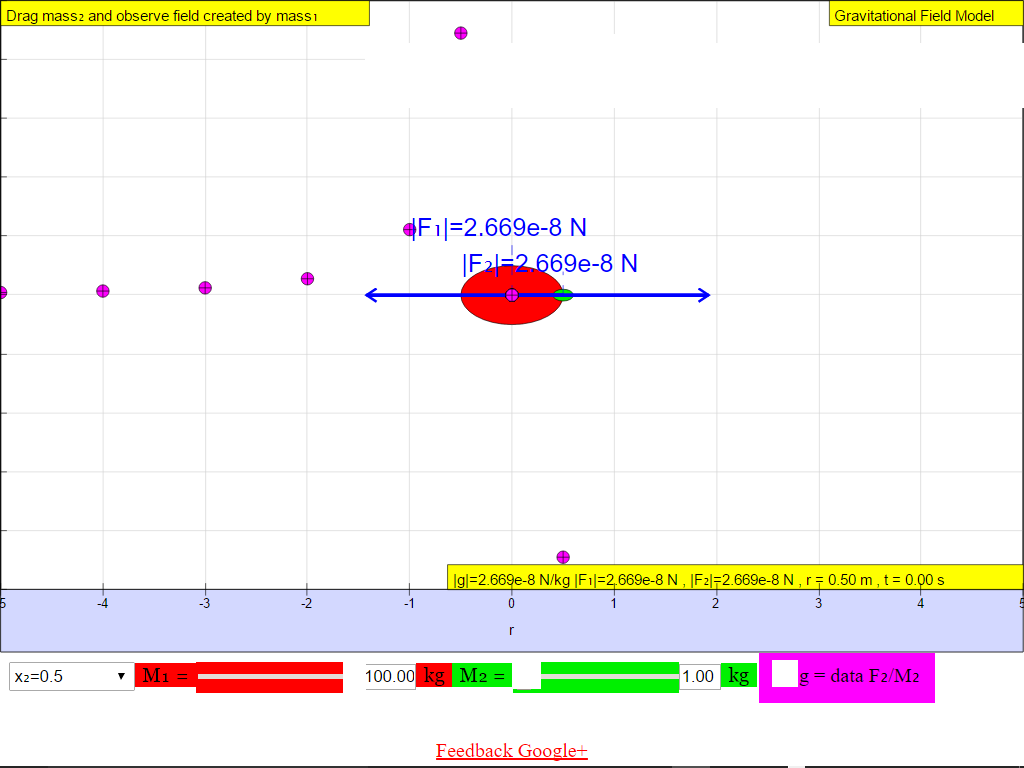
When r = +0.5 m, |g| = 2.669x10^-8 N/kg towards M


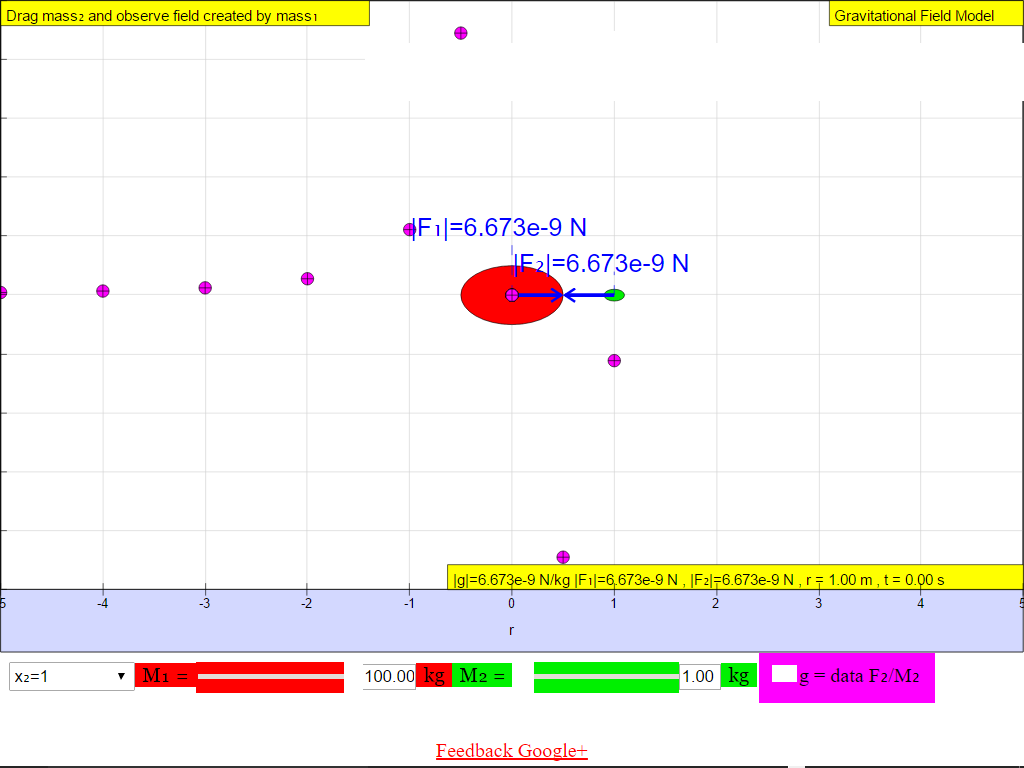
When r = 1.0 m, |g| = 6.673x10^-9 N/kg towards M


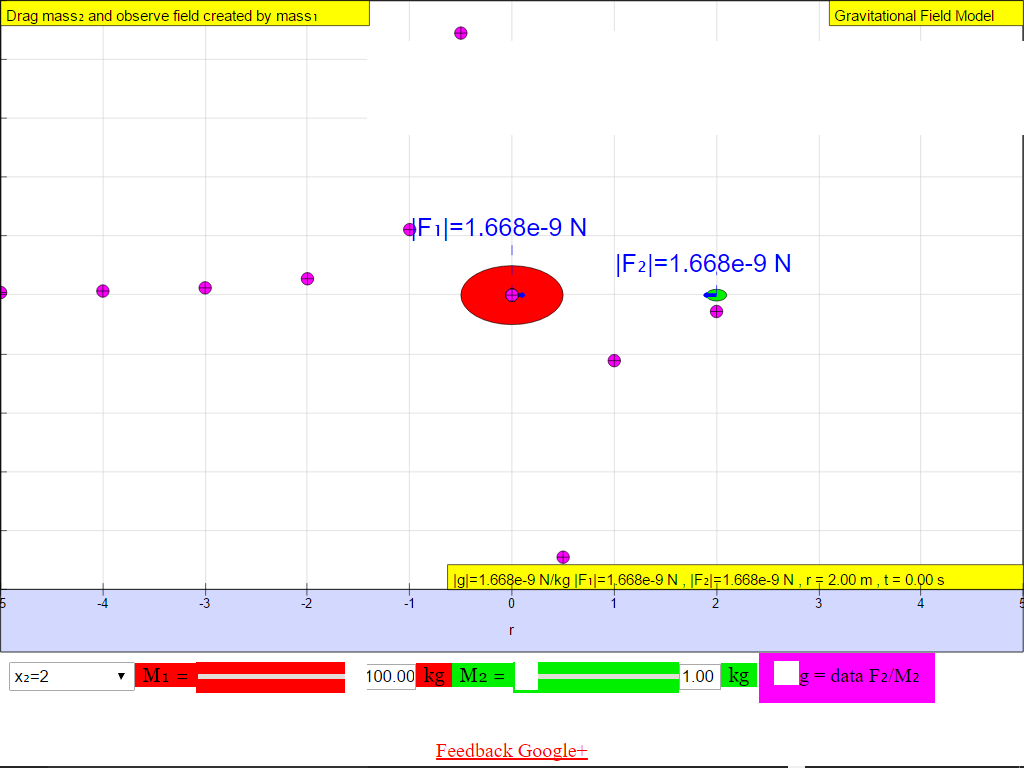
When r = 2.0 m, |g| = 1.668x10^-9 N/kg towards M

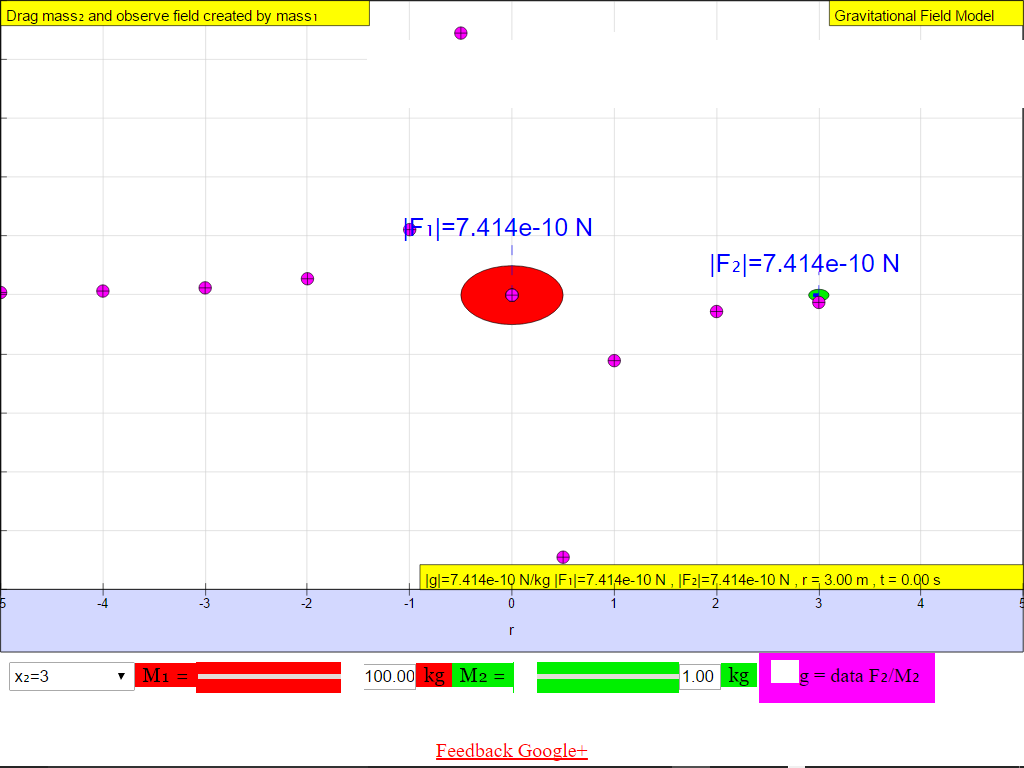
When r = +3.0 m, |g| = 7.414x10^-10 N/kg towards M


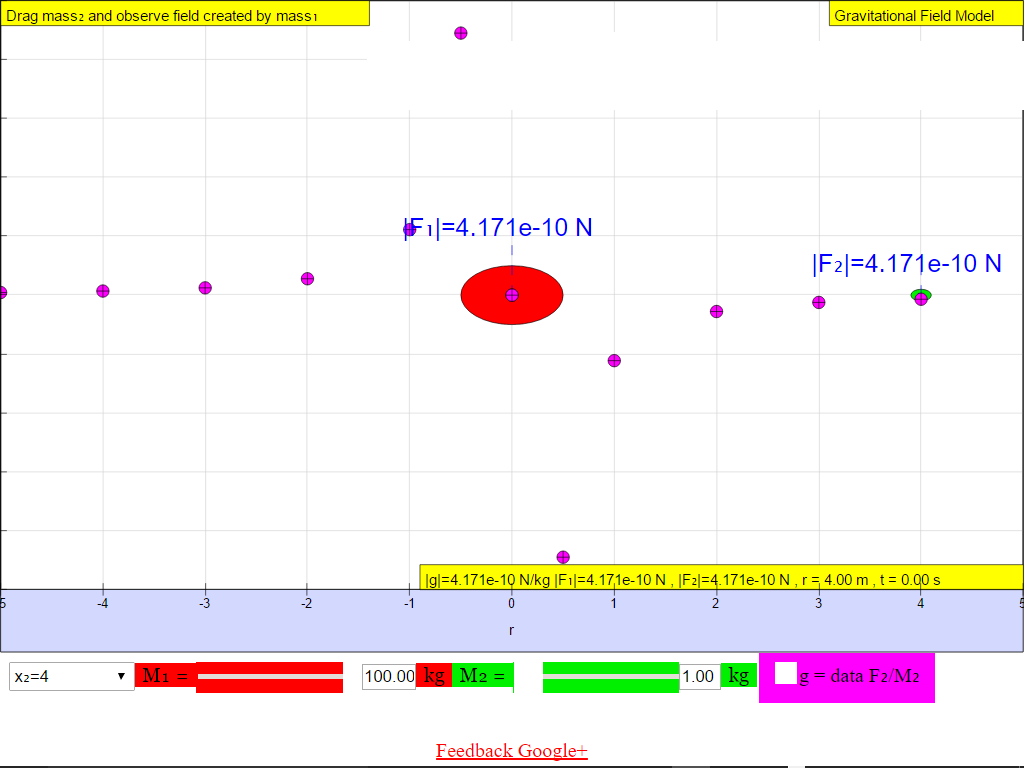
When r = +4.0 m, |g| = 4.171x10^-10 N/kg towards M


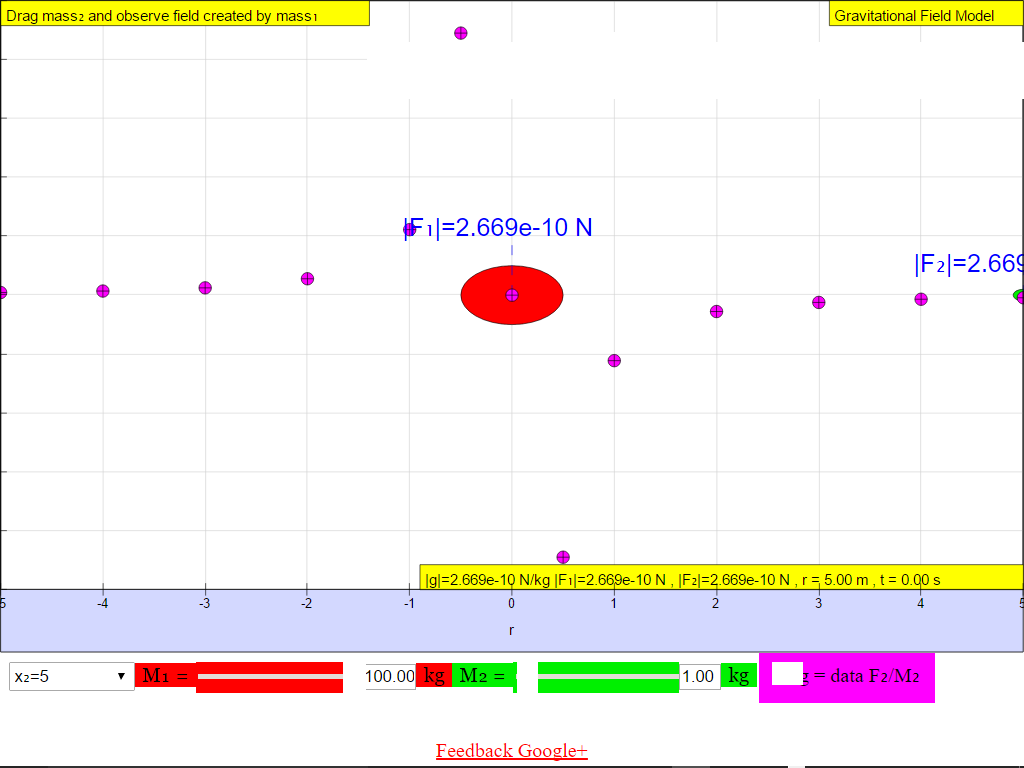
When r = 5.0 m, |g| = 2.669x10^-10 N/kg towards M.

7.2.2.3 Vector Quantity

Suggest whether g field is a vector (possessing both magnitude and direction) or scalar (possessing only magnitude, no direction) quantity.

1)    Gravitational field strength, g (depicted as a magenta color curve) is a vector quantity, and it has a direction which is always towards the mass M.

7.2.2.4 Independent of test mass m

Try varying the values of the green test mass m, does it change the value of g due to mass M alone?

  As shown in  $g=\genfrac{}{}{0.1ex}{}{GM}{r^2}$, the gravitational field strength of source mass M , g is independent of the mass at that point, m. 

7.2.2.5 Modeling activity with Simulation.

From the pictures above, how do the values of g changes with r?
Is the relationship linear, quadratic, inverse square etc?
Try your own model by keying an expression to test  linear = "r", quadratic = "r^2", inverse square = "1/r^2".
Which model seems to "fit" the g well?
The suggested activities is on 7.2.6 Model can you think of a mathematically valid equation to represent the gravitational field strength, g ?

7.2.2.5.1 gravitational field inverse square law field

  The magnitude of the field strength , g varies according to the inverse square law  $gproportional\frac{1}{r^2}$ .Hence gravitational field is also known as an inverse square law field. In other words as r increases, magnitude of g decreases according the formula $g=\frac{GM}{r^2}$

7.2.2.5.2 gravitational field points towards source mass M

•    On the left side of the M =100-kg mass, the gravitational field strength points to the right are positive values.
•    On the right side of the M =100-kg mass, the gravitational field strength points to the left are negative values.
The reason is because of the adoption of the Cartesian coordinate system with positive x direction to the right.

Activity to do

Complete section (A) & (B) in ICT inquiry worksheet 1 using the EJS below to build your conceptual understanding on gravitational field strength. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.

7.2.3 YouTube

https://youtu.be/nZSHpQmlddk video tutorial to explain how to use the simulations for learning the concepts

7.2.4 Inquiry:

An astronaut feels that he is ‘floating’ in a spacecraft in outer space as the spacecraft rotates around the Earth at a distance of 4 x 10⁷ m from the centre of Earth. He concludes that he is ‘floating’ because he is not experiencing any gravitational field of the Earth. Suggest whether his conclusion is right.

7.2.5 YouTube 

https://youtu.be/_ikouWcXhd0 Resource Running in Space! by ReelNASA

7.2.6 Model:

The following suggested activity is recommended to allow students to use mathematical equations or use the model field to propose a mathematically valid equation to represent the gravitational field strength, g.
Hint: try typing in expression like  6.67*100/r^2 (left)  and - 6.67*100/r^2 (right) separately.
Note that students do not need to key in x10^-11.
Note that the model field assumes G = 6.67 instead of 6.67x10^-11,M = 100 kg, r is the distance away from M (red gravitational field source mass)

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/52

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity04/gravity04_Simulation.xhtml

 

Briefing Document: 🍎Gravitational Field Simulation Model

1. Introduction

This document reviews the key concepts and functionalities of the "7.2 Gravitational Field JavaScript HTML5 Applet Simulation Model," a resource from Open Educational Resources / Open Source Physics @ Singapore. The simulation is designed to help students understand gravitational field strength (g) using a visual and interactive approach. This document will cover the definition of gravitational field strength, its properties (vector nature and independence from test mass), and its relationship to the inverse square law. We will also highlight the interactive nature of the model and its use for educational inquiry.

2. Core Concepts

• Gravitational Field Strength (g): The document defines gravitational field strength (g) as "the gravitational force per unit mass acting on a point mass placed at that point." It's measured in N/kg or m/s².
• Quote: "The gravitational field strength, g at a particular point in free space is defined as the gravitational force per unit mass acting on a point mass placed at that point."
• Point Mass Assumption: The use of a 'point mass' is crucial for simplifying analysis because:

1. A point mass does not distort the gravity field of its surrounding.
2. The forces acting on different parts of the point mass are generally the same.

• Quote: "To simplify analysis, point mass are used as they are physically very small so that the point mass itself does not distort the gravity field of its surrounding. Another reason could be that the forces acting on different parts of the point mass are generally the same."
• Relationship to Newton's Law of Gravitation: The document uses Newton's Law of Gravitation to derive the formula for gravitational field strength. Starting with:
• F = G * M * m / r^2
• and knowing that F = mg, the gravitational field strength is derived as:
• g = G * M / r^2
• Graphical Representation: The simulation displays gravitational field strength (g) at various distances (r) from a source mass (M), demonstrating the inverse square relationship between g and r. The document provides specific values for g at different r values, illustrating how the magnitude of g decreases as the distance from mass M increases.
• Vector Nature: Gravitational field strength (g) is a vector quantity. Its direction is always towards the source mass (M). The simulation uses a magenta-colored curve to depict the field, and in the simulation the direction of g is shown by direction on x axis being positive when to the right of source mass M, negative to the left of the source mass M (using the Cartesian coordinate system).
• Quote: "Gravitational field strength, g (depicted as a magenta color curve) is a vector quantity , and it has a direction which is always towards the mass M."
• Independence of Test Mass (m): The strength of the gravitational field (g) due to mass M is independent of the test mass (m) placed in that field. This is evident from the formula g = GM/r², where m does not appear.
• Quote: "As shown in g = G M / r^2, the gravitational field strength of source mass M , g is independent of the mass at that point, m."
• Inverse Square Law: The magnitude of the gravitational field strength (g) varies inversely with the square of the distance (r) from the source mass. This is described as: g ∝ 1/r^2. This principle is emphasized as the core behavior of the gravitational field.
• Quote: "The magnitude of the field strength , g varies according to the inverse square law g proportional 1 / r^2."

3. Simulation and Interactive Learning

• Simulation Model: The resource includes an embedded HTML5 simulation (iframe) allowing users to visualize and interact with a gravitational field.
• Quote: ""
• Modeling Activity: The document encourages users to explore the relationship between g and r by testing different mathematical models (linear, quadratic, inverse square) against the simulation's behavior.
• User Input: Users can input their own mathematical equations to test how well they match the behavior of the g field within the simulation. The document provides a starting point, 6.67*100/r^2 (left of M) and - 6.67*100/r^2 (right of M), and states that the model assumes G = 6.67 instead of 6.67x10^-11, M = 100 kg, and r is the distance away from M.

4. Educational Applications and Inquiry

• Inquiry-Based Learning: The simulation is designed for inquiry-based learning, promoting students to discover the inverse square relationship and vector nature of the gravitational field.
• Worksheet: The document references an ICT inquiry worksheet to accompany the use of the simulation.
• Astronaut Scenario: The document presents a scenario involving an astronaut in orbit to prompt discussions on whether a feeling of ‘weightlessness’ means there is no gravitational field. This underscores the fact that a gravitational field still exists and is responsible for the orbiting motion.
• YouTube Tutorials: The inclusion of YouTube tutorial links highlights the resource's focus on diverse learning styles.
• Quote: "https://youtu.be/nZSHpQmlddk video tutorial to explain how to use the simulations for learning the concepts"
• App Availability: The app is available on Android devices indicating the cross platform nature of the simulation.

5. Technical Details

• Technology: The simulation is a JavaScript HTML5 applet and runs on web browsers as well as mobile devices.
• Credits: The simulation is developed by Anne Cox, Wolfgang Christian, and Francisco Esquembre.
• Licensing: The content is licensed under Creative Commons Attribution-Share Alike 4.0 Singapore License, with separate terms for commercial use of the underlying EasyJavaScriptSimulations library.

6. Conclusion

The "7.2 Gravitational Field JavaScript HTML5 Applet Simulation Model" is a valuable educational tool for understanding gravitational field strength. It combines a clear definition of the concept, mathematical derivation, a visual simulation, and interactive inquiry-based learning opportunities. The resources effectively explains the core physics principles of the gravitational field, emphasizing its inverse square law behavior, vector nature, and independence from the test mass. The availability of YouTube tutorials, ICT inquiry worksheet materials and the cross platform nature of the simulations indicates a well-rounded approach to learning this physics concept.

Gravitational Fields Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. How does the gravitational field strength change as you move further away from a source mass, and what visual representation demonstrates this?
2. Define gravitational field strength and explain its units.
3. Why is the concept of a point mass important when analyzing gravitational fields?
4. Write the equation for the gravitational force between two masses and the equation for gravitational field strength derived from it.
5. Explain what an inverse square law is and why the gravitational field is considered one.
6. Describe the direction of the gravitational field vector in relation to the source mass.
7. Does changing the test mass affect the gravitational field strength? Explain.
8. According to the provided data, what happens to the value of g when the distance (r) is halved?
9. An astronaut in a spacecraft orbiting Earth feels weightless and concludes he is not experiencing Earth's gravitational field. Is this conclusion correct?
10. How can the provided simulation model be used to help students understand the concept of gravitational field strength?

Answer Key

1. The gravitational field strength decreases as you move further from a source mass, and this is illustrated by an increase in the spacing between field lines. This indicates that the force of gravity is weakening with distance.
2. Gravitational field strength is defined as the gravitational force per unit mass acting on a point mass placed at that point. Its units are Newtons per kilogram (N/kg) or meters per second squared (m/s²).
3. Point masses are used to simplify analysis because they are physically small, preventing them from distorting the gravity field of their surroundings. Additionally, the forces acting on all parts of a point mass are generally the same.
4. The gravitational force is given by F = G * M * m / r², and gravitational field strength is given by g = G * M / r², where G is the gravitational constant, M is the source mass, m is the point mass, and r is the distance between them.
5. An inverse square law means that a quantity (like gravitational field strength) is inversely proportional to the square of the distance from its source. In other words, as the distance (r) doubles, the field strength is quartered.
6. The gravitational field strength vector always points toward the source mass that is creating the field. This direction indicates the pull of the gravitational force.
7. No, changing the test mass does not affect the gravitational field strength. The field strength depends only on the source mass and the distance from it, as shown in the formula g = G * M / r².
8. Based on the provided data, when the distance (r) is halved, the magnitude of the gravitational field strength (g) increases by approximately a factor of four. This demonstrates the inverse square relationship.
9. The astronaut's conclusion is incorrect. While he feels weightless, he is still experiencing the gravitational field of the Earth, which causes him and the spacecraft to orbit. The feeling of weightlessness arises because he and the spacecraft are falling towards earth at the same rate.
10. The simulation model allows students to manipulate variables, visualize field lines, and observe how the gravitational field strength changes with distance. This provides a more intuitive and interactive way to understand the concepts.

Essay Questions

Instructions: Answer each question in a well-structured essay format.

1. Discuss the significance of the point mass assumption in the context of gravitational fields. How does this assumption simplify the analysis, and what are its limitations?
2. Explain the relationship between Newton's law of gravitation and the concept of gravitational field strength. Describe the steps in deriving the formula for gravitational field strength from Newton’s law of gravitation.
3. Analyze the inverse square law in relation to gravitational fields. Discuss how the magnitude of the gravitational field strength changes with distance from the source mass and relate this to the given data points.
4. Describe how the simulation model can enhance the teaching and learning of gravitational field strength. Provide specific examples of activities and tasks the model allows, and their contribution to understanding.
5. A common misconception is that astronauts in space are not experiencing any gravity. Explain why this is incorrect and how the concept of gravitational field strength can be used to clarify this misunderstanding.

Glossary of Key Terms

• Gravitational Field Strength (g): The gravitational force per unit mass exerted on a point mass at a specific location in a gravitational field. Its units are Newtons per kilogram (N/kg) or meters per second squared (m/s²).
• Point Mass: An idealized object with mass but no size, used to simplify gravitational calculations by avoiding the complexities of extended bodies.
• Inverse Square Law: A physical law stating that a quantity is inversely proportional to the square of the distance from the source of that physical quantity; gravity is an example.
• Test Mass: A mass used to probe the properties of a gravitational field, typically considered to be small enough so as not to affect the source.
• Source Mass: A mass creating a gravitational field that exerts a force on other objects with mass.
• Vector Quantity: A quantity that has both magnitude and direction, such as gravitational field strength.
• Scalar Quantity: A quantity that has magnitude only, without any direction.
• Newton's Law of Gravitation: A law stating that every particle attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.gravity04app388924&hl=en

Video

https://notebooklm.google.com/notebook/8109787c-d4d8-4b73-88b2-ee811437f5a1/audio

Timeline of Main Events and Concepts

• Prior to the Simulation (Implied):Newton's Law of Gravitation is established.
• The concept of gravitational field strength is developed.
• Introduction of the Simulation Model:A JavaScript HTML5 applet simulation model (gravity04) is created to visualize and explore the concept of gravitational fields.
• The simulation is made accessible on various platforms including desktops, laptops, tablets, and smartphones.
• Core Concepts Illustrated by the Simulation:The gravitational field strength (g) decreases with distance from the source mass (M).
• The field strength (g) is a vector quantity, always pointing towards the source mass.
• The field strength (g) is independent of the test mass (m).
• The relationship between field strength (g) and distance (r) follows an inverse square law (g ∝ 1/r^2).
• Simulation Activities:Users are prompted to model the gravitational field strength by inputting different mathematical expressions.
• Students are prompted to complete activities in an ICT inquiry worksheet.
• Users are prompted to adjust parameters in the simulation (e.g. the distance from source mass, the magnitude of the source mass).
• Supporting Resources:A YouTube video tutorial is provided to explain how to use the simulation.
• A ReelNASA YouTube video is provided as a resource.
• Inquiry-Based Learning:A scenario involving an astronaut in space is presented to challenge students' understanding of gravity.
• Application and Development:The simulation is mentioned as a part of a larger project to create interactive educational tools for STEM education.
• Various other simulation models are listed, suggesting an ongoing effort to create interactive teaching resources.
• Ongoing Efforts:Work is being done to convert Java worksheet customizations to HTML5.
• WebEJS workshops are being held to teach educators how to create simulations

Cast of Characters

• Isaac Newton: Although not explicitly mentioned, Newton is the originator of the law of gravitation on which the simulation is based, making him a key, though invisible, figure.
• Anne Cox: Listed as a credit, indicating involvement in the development of this simulation or the educational resources in general.
• Wolfgang Christian: Listed as a credit, indicating involvement in the development of this simulation or the educational resources in general.
• Francisco Esquembre: Listed as a credit, indicating involvement in the development of this simulation or the educational resources in general. Additionally he is mentioned as a supporter of a WebEJS workshop suggesting a role in the creation and promulgation of the simulation environment in general.
• lookang: A user on the site who has contributed significantly, with a high number of articles and views. It is likely the main coordinator and contributor to this open-source educational resource.
• Various Educators and Developers (Implicit): A number of other names appear in the listing of apps, projects, presentations, and workshops. These highlight an ongoing community that is building and testing simulations for educational use. They are responsible for developing resources based on the EJS simulation technology. They are not characters in the source but are essential in understanding the wider context of this simulation project.

Frequently Asked Questions about Gravitational Fields

1. What is gravitational field strength and how is it defined? Gravitational field strength (denoted as 'g') at a point in space is defined as the gravitational force per unit mass experienced by a point mass placed at that location. It essentially describes the strength of the gravitational pull exerted by a source mass, like a planet, at any point around it. The units for gravitational field strength are Newtons per kilogram (N/kg) or meters per second squared (m/s²).
2. Why is a 'point mass' assumption necessary when analyzing gravitational fields? The point mass assumption simplifies the analysis of gravitational fields. Point masses are treated as if their entire mass is concentrated at a single point. This assumption is used for two primary reasons: Firstly, it ensures that the point mass's own gravitational field doesn't significantly distort the gravitational field being analyzed. Secondly, assuming a point mass means that the gravitational forces acting on all parts of the object are nearly identical, allowing for easier mathematical treatment.
3. How is gravitational field strength related to Newton's Law of Gravitation? The gravitational force between two masses, M and m, is given by Newton's law of gravitation: F = G * M * m / r², where G is the gravitational constant, M is the source mass, m is the point mass, and r is the distance between their centers. Since gravitational field strength 'g' is the gravitational force F per unit mass m (g = F/m), we can combine this with Newton's law to derive the formula for gravitational field strength: g = G * M / r². This equation shows that the gravitational field strength decreases as the square of the distance from the source mass increases, and also that it is proportional to the source mass.
4. Is gravitational field strength a vector or a scalar quantity? Gravitational field strength is a vector quantity. This means it has both magnitude and direction. The magnitude represents the strength of the field (the acceleration experienced by an object), while the direction is always towards the source mass creating the field.
5. How does the distance from the source mass affect the gravitational field strength? The magnitude of the gravitational field strength is inversely proportional to the square of the distance (r) from the source mass. This is known as the inverse square law (g proportional to 1/r²). As the distance increases, the magnitude of 'g' decreases rapidly. The field lines become more spaced out, illustrating that the gravitational influence gets weaker as you move away from the source.
6. Does the test mass have an effect on gravitational field strength? The gravitational field strength (g) due to a source mass (M) is independent of the test mass (m). Although the gravitational force on the test mass is proportional to the test mass, when calculating field strength, we are dividing the force by this same test mass, leaving us with g = G * M / r². Therefore the test mass cancels out and has no impact on the gravitational field of the source mass. This also means that all objects regardless of their masses, will experience the same acceleration at the same point in a gravitational field.
7. What does it mean when we say the gravitational field is an inverse square law field? The term "inverse square law field" refers to the relationship between the magnitude of the gravitational field strength (g) and the distance (r) from the source mass. As mentioned earlier, 'g' is proportional to 1/r². This inverse square relationship means that as the distance from the source mass doubles, the field strength reduces to one-quarter of its original value. This behavior is fundamental to understanding how gravitational forces behave in space.
8. An astronaut feels 'weightless' in orbit, does this mean there is no gravitational field present? No, 'weightlessness' experienced by an astronaut in orbit doesn't mean there is no gravitational field. The astronaut is still within Earth's gravitational field. The 'weightlessness' is due to the fact that the spacecraft, astronaut, and everything else inside are all in a state of freefall, continuously falling towards Earth. However, as they travel at a very high speed, they also continue to curve around the planet, thereby falling around the earth, instead of towards the surface. Because there is no ground reaction force acting against the pull of gravity, the astronaut feels no sensation of weight. Thus the astronaut experiences the sensation of 'floating' even though they are still very much under Earth's gravity.