About

7.4 Satellite in Circular Orbits

7.4.1 Introduction

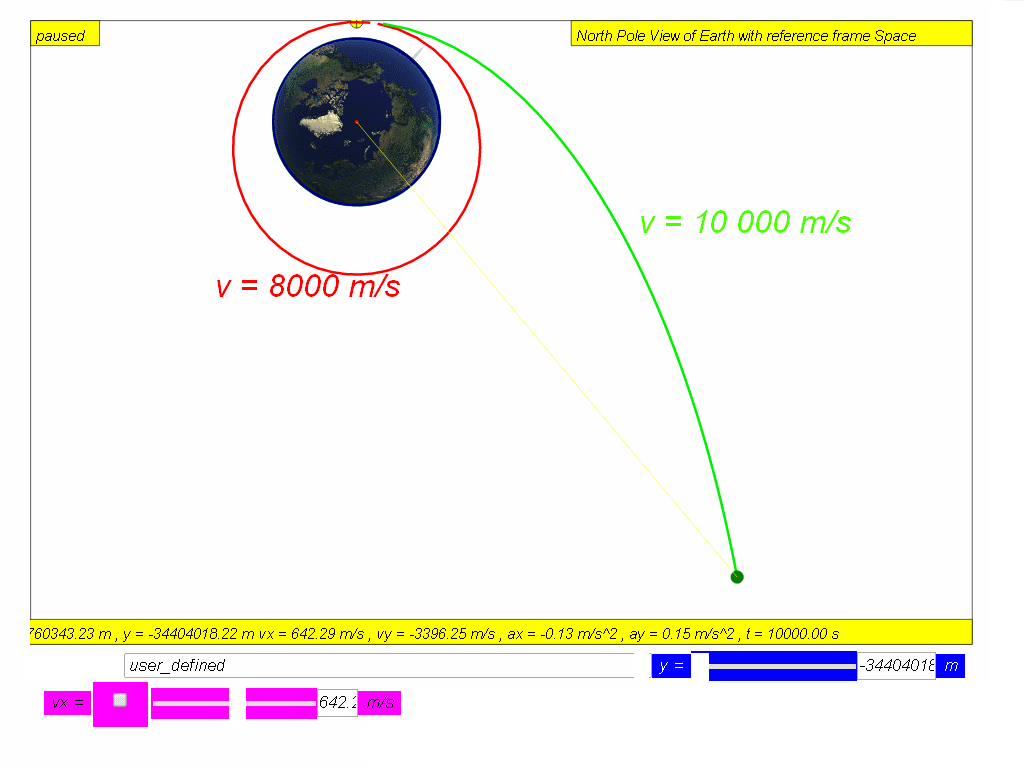
An object projected horizontally near the Earth’s surface follows parabolic trajectories as shown ( v = 0 red, v = 2000 green, v = 4000 blue, v = 6000 yellow and v = 8000 teal) .

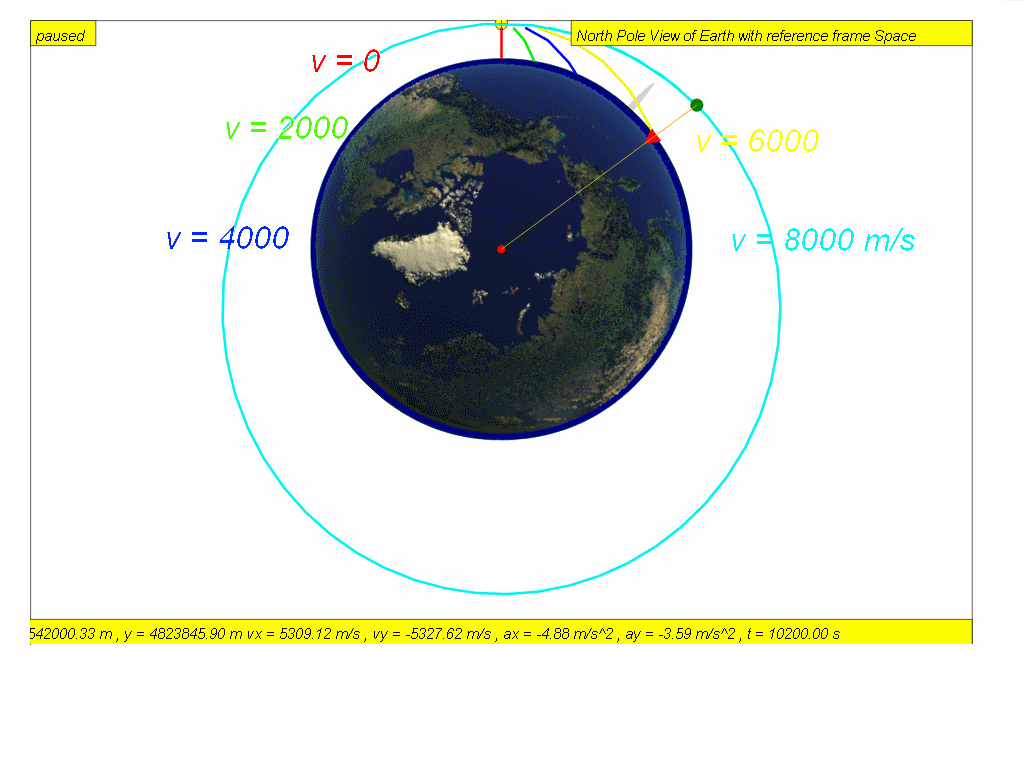
As the speed of projection v increases, the object will reach a speed approximately v = 7888 m/s where the trajectory follows the curvature of the Earth’s surface. [click this for live action now? require internet or scroll down to the model running from hard disk]

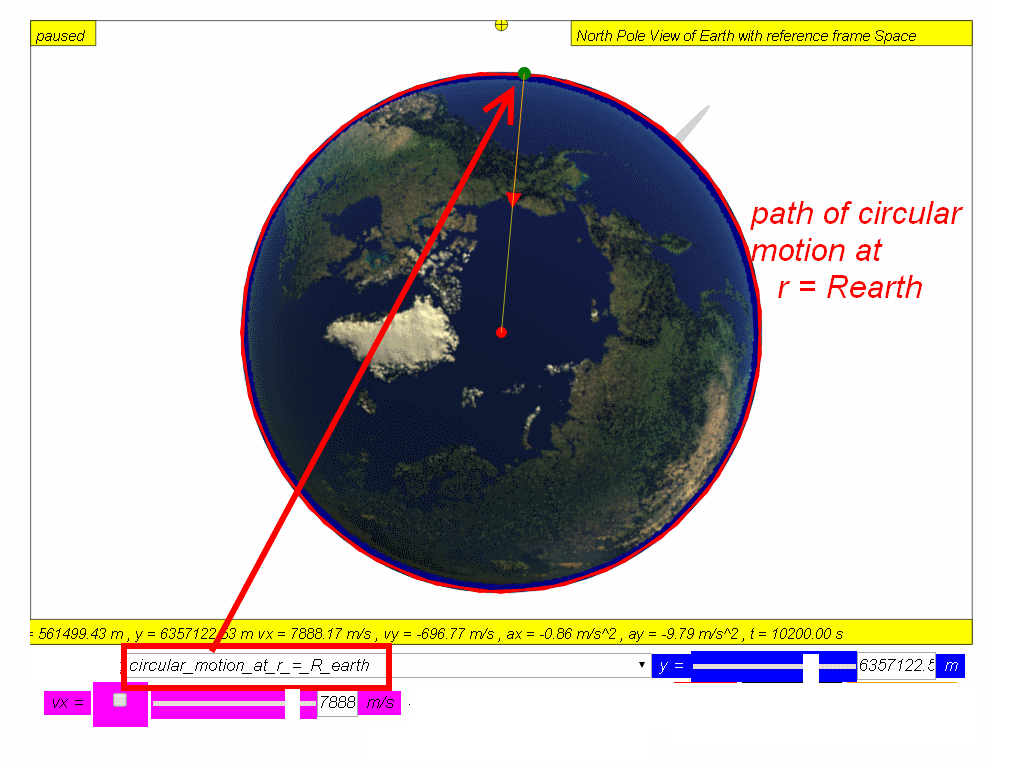
If air resistance is negligible, the object will orbit round the Earth continuously and will never meet the Earth’s surface such as speed v 8000  red m/s and v = 10000 m/s green.

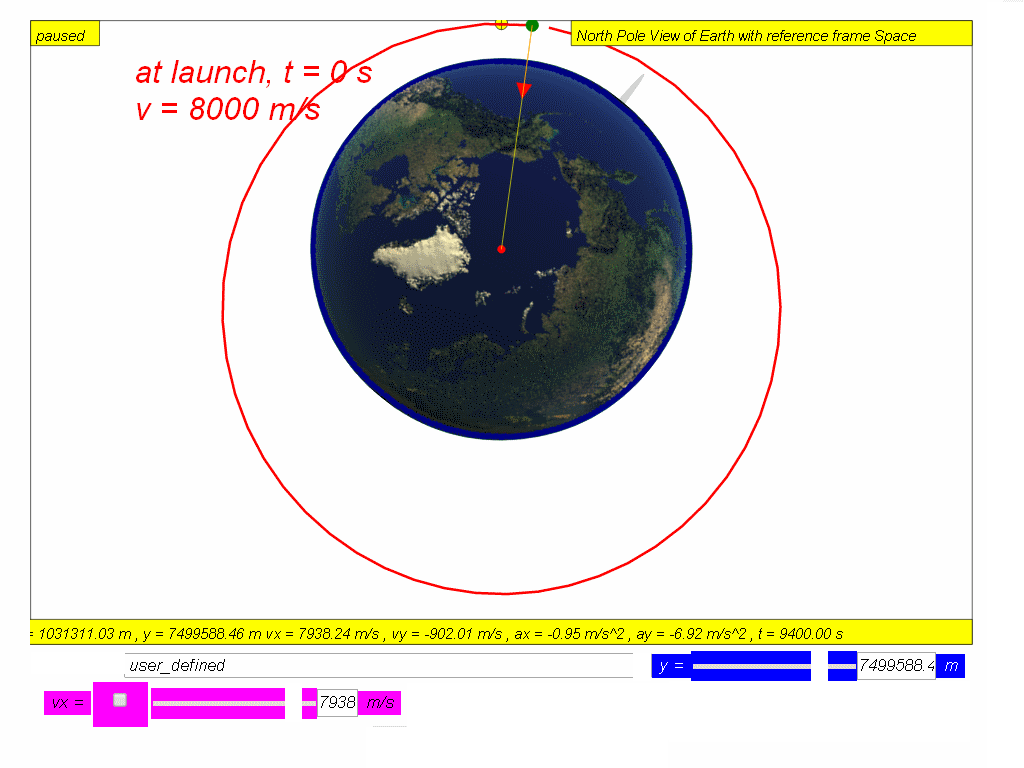
Many man-made satellites move in circular orbits around the Earth. The first man-made satellite, the Sputnik 1, was launched by Soviet Union in 1957. Since then, thousands of satellites have been launched into orbit around the Earth. The only force acting on a satellite in a circular orbit (achieved by launching horizontally at vx =7276.69 m/s at height above Earth surface  H = 0.185 R_E where R_E = 6370 000 m is the radius of Earth,  is the Earth’s gravitational force. The gravitational force (red arrow is directed towards the centre of Earth) is also the the centre of the circular orbit.

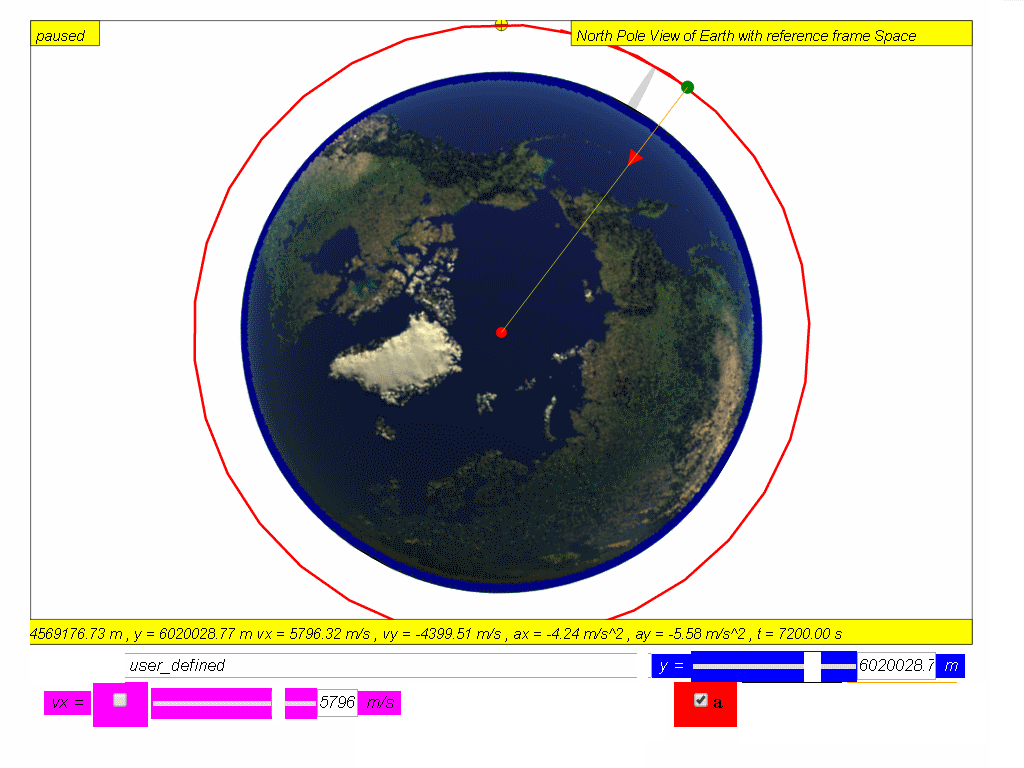
Since the satellite velocity (magenta arrow)  is perpendicular to the gravitational force (Red arrow), its magnitude of velocity remains constant while its direction changes. 

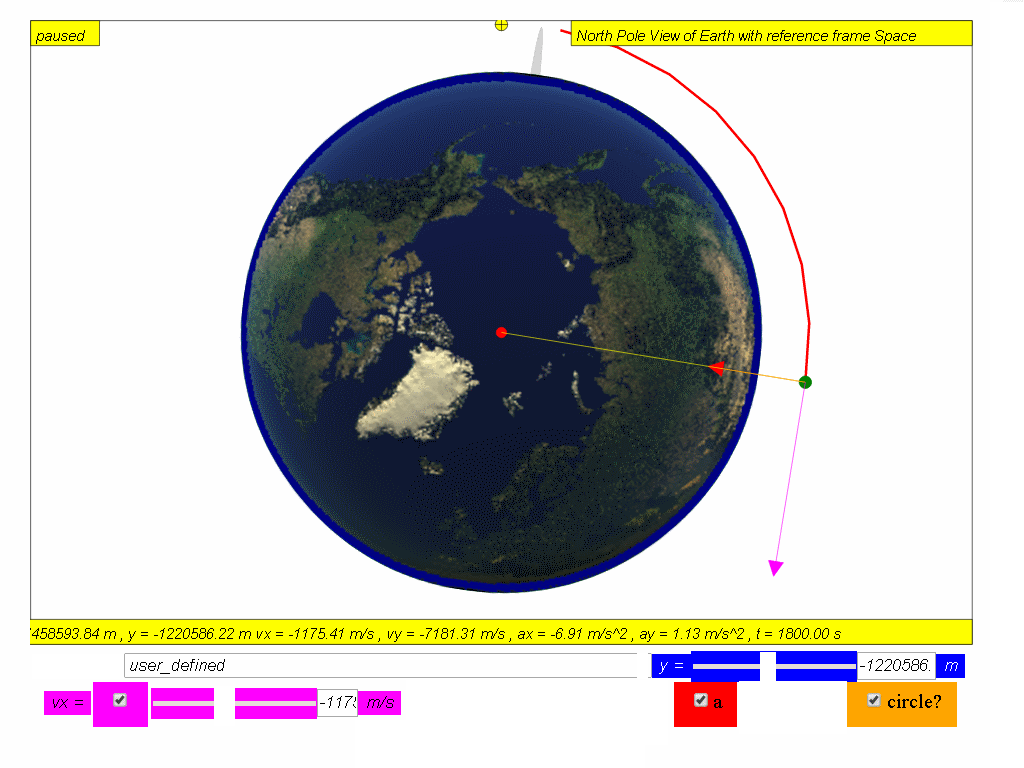
This means that the satellite is traveling in a uniform circular motion .  At the same time, the distance from the satellite to the centre of Earth will also remain constant in this circular orbit.

For a satellite (or any object) in circular orbit, the gravitational force acting on it is the centripetal force that keeps it in circular motion.

Using Newton's second law in this context of a circular motion orbit.

$F=\genfrac{}{}{0.1ex}{}{m{v}^2}{r}$

Since in outer space, the assumption is only Earth's gravitational field is responsible for the circular motion and gravitational force is $F=\genfrac{}{}{0.1ex}{}{GmM}{r^2}$

thus, $\genfrac{}{}{0.1ex}{}{GmM}{r^2}=\genfrac{}{}{0.1ex}{}{m{v}^2}{r}$

the expression can be simplified to give the exact velocity required for circular motion  $\sqrt{\genfrac{}{}{0.1ex}{}{GM}{r}}=v$ .

This equation-formula can be used to calculate the speed required for any object to orbit around a planet of mass M at a constant distance-radius of orbit r

where r is the radius of orbit from the centre of Planet M,
M is the mass of Planet M, which is typically Earth.

7.4.2 Inquiry:

What will happen to the orbiting satellite if it starts to slow down? A student says the gravitational force will be higher than the required centripetal force to keep it in the uniform circular motion. Hence the satellite will be pulled closer towards Earth and move in a smaller circular orbit. Explain with evidences from the model whether the answer is satisfactory.
[click this for live action now? require internet or scroll down to the model running from hard disk]

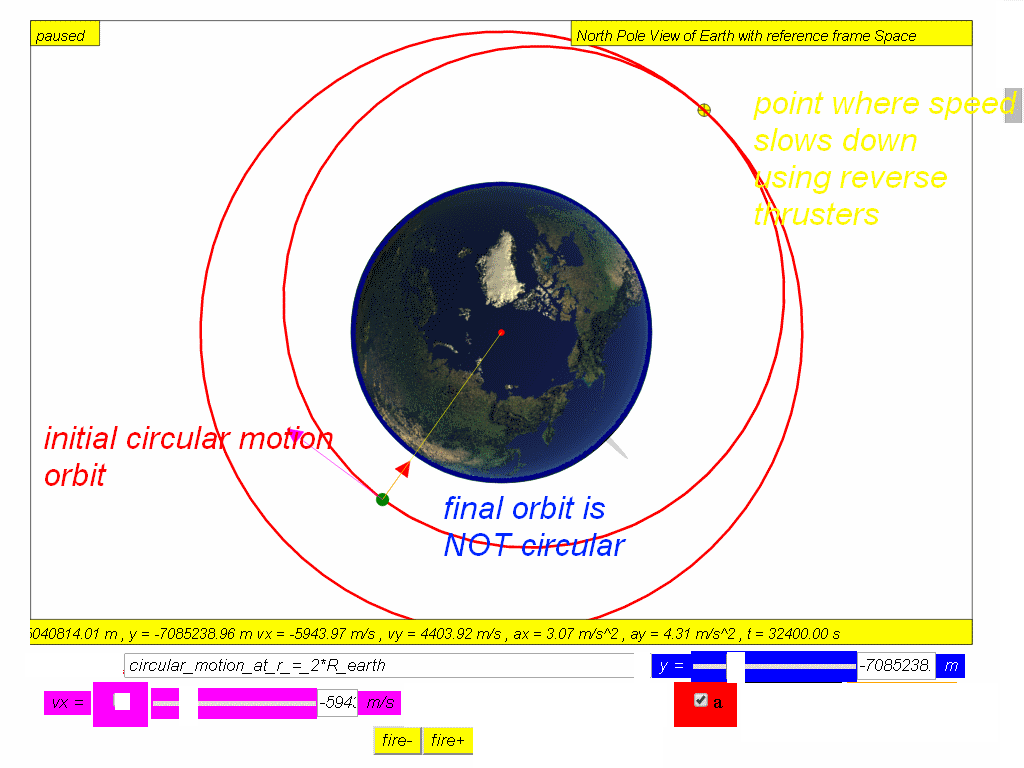
7.4.2.1 Suggested Steps to conduct inquiry

1. Select from drop-down menu option circular_motion_at_r_=_2*R_earth
2. Click play and observe the motion of the orbit. describe the motion is circular or otherwise.
3. Pause the simulation
4. Click fire- to simulate firing of reverse thrusters for a very short time, to reduce the speed of the object in orbit.
5. Observe the motion of the new orbit. describe the motion is circular or otherwise.
6. Design an alternative inquiry option and write down briefly what you have found out.
7. Discuss with more classmates in the school and suggest an a community of learners what you have concluded from the evidences collected by at least 3 other independent approach/options.

The desired outcome is to allow the students to experience real orbits are not always perfectly circular (a common misconception for students). Real life orbits are usually elliptical.

7.4.2.2 Calculation of speed at r = 3 times Radius of Earth

Example 10 (Object in orbit)
How fast must the satellite be moving in its circular orbit about the Earth, if it stays at a constant height of three times of Earth’s radius, above the Earth’s surface? 
(Given:  mass of Earth = 6.0 x 10²⁴ kg; radius of Earth = 6.4 x 10⁶ m)

Suggested Steps to solve this problem

1. draw a free body diagram of the mass and its path (is it circular, linear etc?).
2. decide on the symbols and values, r = 4(6.4 x 10⁶) = 2.56x10⁷ m
3. recall the formula and derive from newton's law $\genfrac{}{}{0.1ex}{}{GmM}{r^2}=\genfrac{}{}{0.1ex}{}{m{v}^2}{r}$
4. substitute the values $\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(6.0x10^{24}\right)}{{\left(2.56x10^7\right)}^2}=\genfrac{}{}{0.1ex}{}{v^2}{2.56x10^7}$
5. imply 3.94x10³ m/s = v
6. check the answer, put v back to check if $\genfrac{}{}{0.1ex}{}{GmM}{r^2}=\genfrac{}{}{0.1ex}{}{m{v}^2}{r}$still hold for both left and right hand sides of the equal sign.

7.4.2.3 Model

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/284

 

Translations

Code	Language		Translator	Run

Credits

Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity08/gravity08_Simulation.xhtml

Briefing Document: 🛰️Satellite Motion Simulation

1. Introduction

This document reviews a resource from Open Educational Resources / Open Source Physics @ Singapore, specifically focusing on a JavaScript HTML5 applet simulation model titled "7.4 Satellite in Circular Orbits." This simulation is designed to help students understand the principles of satellite motion, particularly in circular orbits, and how these motions relate to gravity and centripetal force. The resource also encourages inquiry-based learning by challenging users to explore what happens when a satellite's velocity changes.

2. Key Concepts and Ideas

• Projectile Motion and Orbital Velocity: The simulation demonstrates how objects projected horizontally near the Earth's surface follow parabolic trajectories. As the initial horizontal velocity increases, the trajectory becomes less parabolic.
• Quote: "An object projected horizontally near the Earth’s surface follows parabolic trajectories as shown ( v = 0 red, v = 2000 green, v = 4000 blue, v = 6000 yellow and v = 8000 teal)."
• Circular Orbits: A specific velocity (approximately 7888 m/s according to the text, though it gives 7276.69 m/s elsewhere) results in the trajectory matching the curvature of the Earth, leading to a circular orbit. In a circular orbit, the satellite continuously falls toward Earth but also moves forward, effectively orbiting.
• Quote: "As the speed of projection v increases, the object will reach a speed approximately v = 7888 m/s where the trajectory follows the curvature of the Earth’s surface."
• Quote: "If air resistance is negligible, the object will orbit round the Earth continuously and will never meet the Earth’s surface such as speed v 8000 red m/s and v = 10000 m/s green."
• Gravity as Centripetal Force: The simulation highlights that the only force acting on a satellite in a circular orbit (assuming negligible air resistance) is Earth's gravitational force. This gravitational force also provides the necessary centripetal force to keep the satellite in its circular path.
• Quote: "The only force acting on a satellite in a circular orbit ... is the Earth’s gravitational force. The gravitational force (red arrow is directed towards the centre of Earth) is also the the centre of the circular orbit."
• Quote: "For a satellite (or any object) in circular orbit, the gravitational force acting on it is the centripetal force that keeps it in circular motion."
• Constant Speed and Changing Direction: While the speed of a satellite in a circular orbit is constant, its velocity is constantly changing due to the change in direction. The satellite's velocity (magenta arrow) is always perpendicular to the gravitational force (red arrow).
• Quote: "Since the satellite velocity (magenta arrow) is perpendicular to the gravitational force (Red arrow), its magnitude of velocity remains constant while its direction changes."
• Mathematical Relationship: The simulation relates the concepts of orbital speed to the planet's mass and the radius of the orbit through equations derived from Newton's Laws, specifically:
• F = mv^2/r (Centripetal Force)
• F = GMm/r^2 (Gravitational Force)
• By setting these equal, GM/r = v^2 This allows for calculation of the orbital velocity at a given orbital radius.
• Non-Circular Orbits (Elliptical Orbits): The simulation challenges the common misconception that all orbits are perfectly circular. It prompts inquiry into what happens when a satellite's speed changes, revealing that a decrease in speed results in the satellite falling into a smaller, usually elliptical orbit.
• Quote: "The desired outcome is to allow the students to experience real orbits are not always perfectly circular (a common misconception for students). Real life orbits are usually elliptical."
• Inquiry-Based Learning: The simulation is designed to be interactive, with a specific inquiry activity. Users are encouraged to use the model to explore the effect of a speed change via simulated reverse thrusters on a satellite’s path. It provides suggested steps to guide inquiry and to promote discussion.
• Quote: "What will happen to the orbiting satellite if it starts to slow down? A student says the gravitational force will be higher than the required centripetal force to keep it in the uniform circular motion. Hence the satellite will be pulled closer towards Earth and move in a smaller circular orbit . Explain with evidences from the model whether the answer is satisfactory."

3. Simulation and Learning Activities

The simulation provides the following elements:

• Interactive Model: The HTML5-based simulation is accessible on various platforms (including mobile) and allows users to manipulate variables and observe the outcomes in real-time.
• Suggested Inquiry Steps: The document outlines specific steps for students to follow to explore the effects of changing velocity, which encourages active and analytical learning.
• Problem Solving: An example calculation (Example 10) shows how to calculate the orbital speed for a satellite at a specific height. This section highlights the use of equations and free-body diagrams in solving physics problems.
• Alternative Inquiry Options: Students are prompted to design their own inquiry, which encourages critical thinking and independent learning.
• Community of Learners: The resource advocates for discussing findings with classmates to develop a collaborative learning environment.
• Links to Other Resources: The document contains links to other physics simulations and interactive resources, including the older java version.

4. Technical Details

• Platform: The simulation runs on JavaScript HTML5 and is designed to be cross-platform.
• Credits: The model credits Todd Timberlake, lookang, and fu-kwun hwang.
• Licensing: The material is licensed under Creative Commons Attribution-Share Alike 4.0 Singapore License.

5. Educational Value

The resource provides an engaging and interactive way for students to:

• Visualize abstract concepts (like gravity, centripetal force, and orbital motion).
• Explore the relationship between theoretical physics and real-world scenarios.
• Develop critical thinking through inquiry-based learning.
• Enhance problem-solving skills through example calculations.
• Collaborate with peers and build a community of learners.
• Correct a common misconception about orbits always being circular.

6. Conclusion

This simulation model is a valuable educational tool for teaching the principles of satellite motion and the associated physics concepts. It uses an interactive approach to encourage active learning and critical thinking, and promotes a deeper understanding of orbital mechanics. The resource’s emphasis on inquiry and exploration ensures that students are not passively absorbing information, but are actively participating in their own learning process.

 

Satellite Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What type of path does an object follow when projected horizontally near the Earth's surface with insufficient speed to achieve orbit?
2. What is the primary force acting on a satellite in a circular orbit?
3. What is the relationship between the velocity and the gravitational force on a satellite in a circular orbit?
4. What is the role of gravitational force in the context of circular motion of a satellite?
5. What happens to the speed of a satellite in a circular orbit?
6. Explain why a satellite maintains a constant distance from Earth in a circular orbit?
7. In the context of satellite motion, what is meant by "centripetal force?"
8. What happens to the orbit of a satellite if its speed decreases?
9. According to the text, what is a common misconception about satellite orbits that students have?
10. What is the key takeaway from the simulation regarding the shapes of real satellite orbits?

Quiz Answer Key

1. An object projected horizontally near Earth’s surface follows a parabolic trajectory when it lacks the speed necessary to orbit. This path curves towards the Earth due to gravity.
2. The primary force acting on a satellite in a circular orbit is the Earth's gravitational force. This force constantly pulls the satellite towards the center of the Earth.
3. The velocity of a satellite in a circular orbit is perpendicular to the gravitational force. This results in a consistent change in direction but a constant speed.
4. In the circular motion of a satellite, the gravitational force acts as the centripetal force. This force is always directed toward the center of the circle, causing the satellite to move in a circular path.
5. The speed of a satellite in a circular orbit remains constant as long as the orbital radius does not change. This constancy exists because the gravitational force does not act to speed up or slow down the object.
6. A satellite maintains a constant distance because its velocity is always perpendicular to the gravitational force. These forces together create a circular path around Earth at a consistent radius.
7. Centripetal force is the force that is required to keep an object moving in a circular path. It is always directed towards the center of the circular path. In the case of satellite motion, this is gravitational force.
8. If a satellite's speed decreases, the gravitational force will become greater than the required centripetal force causing it to be pulled closer to Earth, moving in a smaller, potentially elliptical orbit.
9. A common misconception that students have is that satellite orbits are always perfectly circular. In fact, real satellite orbits are more often elliptical than circular.
10. The simulation demonstrates that real satellite orbits are not always perfectly circular but are often elliptical, which can be observed when the satellite's speed is altered.

Essay Questions

Instructions: Answer the following questions in essay format using your understanding of the source material.

1. Explain the relationship between the initial velocity of a projectile and its resulting trajectory, specifically discussing the transition from parabolic motion to circular orbits.
2. Analyze the forces acting on a satellite in a circular orbit. Discuss how these forces maintain the satellite’s motion and what happens when these forces are not balanced.
3. Describe the mathematical relationship that governs the speed required for a satellite to maintain a circular orbit. How do changes in radius affect the required speed?
4. Using the simulation, describe what happens to a satellite’s orbit when a reverse thruster is briefly fired. Explain why this change occurs in terms of centripetal and gravitational forces.
5. Discuss how the provided simulation helps clarify real satellite orbits. How does this understanding challenge common student misconceptions about the geometry of orbits?

Glossary of Key Terms

Centripetal Force: The force that acts on a body moving in a circular path and is directed toward the center of the circle. In the context of satellites, this force is provided by gravity.

Circular Orbit: A path around a celestial body where the orbiting object maintains a constant distance from the center of the body, tracing a perfect circle.

Elliptical Orbit: A path around a celestial body where the orbiting object’s distance from the center of the body varies, tracing an oval-shaped path rather than a circle.

Gravitational Force: The attractive force between two objects with mass. In the case of a satellite, this is the force exerted by Earth that pulls the satellite toward its center.

Parabolic Trajectory: The path followed by an object thrown or projected near the Earth's surface, where the only force acting on it is gravity. The path is a U-shaped curve.

Satellite: An object that orbits a planet or other celestial body. Satellites can be natural (like the Moon) or artificial (like man-made communication satellites).

Uniform Circular Motion: The motion of an object moving in a circle at a constant speed. This motion requires a force, such as gravity for orbiting bodies, that is always directed towards the center of the circle.

Velocity: The speed and direction of an object's motion. In the context of circular motion, the satellite's velocity is always tangent to its orbital path.

 App

https://play.google.com/store/apps/details?id=com.ionicframework.gravity08app871221&hl=en

Versions:

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar (older Java version, not updated anymore!, click the download model button just below the picture to get the HTML5 version)

Other resources

1. http://physics.weber.edu/schroeder/software/NewtonsCannon.html
2. http://www.physicsclassroom.com/Physics-Interactives/Circular-and-Satellite-Motion/Uniform-Circular-Motion/Uniform-Circular-Motion-Interactive
3. https://cosci.tw/run/?name=axcSN41469081156263&fbclid=IwAR0WFDGdROUeqVzBGwKuCGGSgfVlaXjKS_iX_OFJWdhyo96M1gTvJELRQg8 Centripetal Force - Sputnik Track & Cycle:
4. https://cosci.tw/run/?name=Plr6hg1452128704066&fbclid=IwAR1gm70w9OFG7_4tJnJbm_GBhfN6heqNQTZGZVWdlrDnn6LJd-SyV7H1Do0 Surface Gravity

Frequently Asked Questions about Satellite Orbits

1. What force keeps a satellite in orbit around the Earth, and what direction does it point? The primary force keeping a satellite in a circular orbit is Earth's gravitational force. This force is always directed towards the center of the Earth, which is also the center of the circular orbit. It acts as the centripetal force required to keep the satellite moving in a circular path rather than a straight line.
2. How does the velocity of a satellite relate to its circular orbit? For a stable circular orbit, the satellite's velocity must be perpendicular to the gravitational force. The magnitude (speed) of the satellite's velocity remains constant, and the distance from the satellite to the center of the Earth will also stay constant. This means the satellite is in uniform circular motion. The specific speed required is dependent on the radius of the orbit, with faster speeds required for lower orbits.
3. What is the relationship between the gravitational force and the centripetal force in a satellite's orbit? In the context of a satellite in circular orbit, the gravitational force acting on the satellite is the centripetal force. This is what keeps it in its circular motion. This relationship can be expressed mathematically as GmM/r² = mv²/r, where G is the gravitational constant, m is the satellite's mass, M is the Earth's mass, r is the orbital radius, and v is the satellite's velocity.
4. How can the orbital speed of a satellite be calculated? The orbital speed (v) of a satellite can be derived from the equation equating gravitational force and centripetal force: GmM/r² = mv²/r. This simplifies to v = sqrt(G*M/r), where G is the gravitational constant, M is the mass of the planet (usually Earth), and r is the radius of the orbit (distance from the satellite to the center of Earth). Using this formula you can calculate the exact speed required for a satellite to orbit at a given radius.
5. What happens if a satellite in orbit slows down? If a satellite slows down, the gravitational force becomes greater than the centripetal force needed to maintain its current orbit. Consequently, the satellite will be pulled closer to the Earth and move into a smaller orbit. This new orbit will have a different speed and orbital radius than before. The simulation of a satellite firing reverse thrusters demonstrates this shift.
6. Why are real satellite orbits not always perfectly circular? While the calculations and ideal models often assume circular orbits, real-life orbits are frequently elliptical, meaning they are oval-shaped instead of perfectly circular. This occurs for various reasons, including variations in launch conditions, atmospheric drag, and gravitational interactions with other celestial bodies.
7. What happens to a satellite's orbit if it's not launched with the correct horizontal velocity? The simulation shows objects launched horizontally at different speeds. If a projectile is not launched fast enough, it will follow a parabolic path back to earth. A critical horizontal speed (approximately 7888 m/s near the Earth's surface) is necessary to match the curvature of the Earth for a stable orbit. If too slow, the projectile returns to Earth; if too fast, the projectile will achieve a different (usually higher) orbit, including potentially escaping Earth's orbit.
8. What educational resources are available to understand satellite motion and gravity? There are numerous open educational resources available online, including interactive simulations, applets, and modeling tools like the one referenced in the source. These resources allow users to explore and visualize satellite orbits and related physics concepts through experimentation. These simulation models are designed to improve student understanding of complex ideas by allowing them to investigate these concepts in action.