Breadcrumbs

About

gravity09

7.5 Kepler’s Third Law

7.5.1 Newton's Second Law in Circular Motion to derive Kepler’s Third Law T² α r³

By analysing the free body diagram of a satellite in circular orbit, the equation for Newton's Second Law is,

i.e.              ΣF = mrω²
            $\frac{G m M}{r^{2}} = m r ω^{2}$

Recalling in circular motion angular velocity and its period are related as follow, $ω = \frac{2 π}{T}$
Hence,      $\frac{G m M}{r^{2}} = m r ω^{2} = m r {(\frac{2 π}{T})}^{2}$

Which can be simplified to an equation involving T and r

$T^{2} = \frac{4 π^{2}}{G M} r^{3}$

This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit is directly proportional to the cube of the radius of its orbit. T² α r³

7.5.1.1 Note:

The Kepler’s Third Law T² α r³is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it and thus it acts as the centripetal force.

7.5.1.2 Activity

Complete ICT inquiry worksheet 2 to build your conceptual understanding on Kepler’s Third Law.

7.5.1.3 Steps to support your inquiry

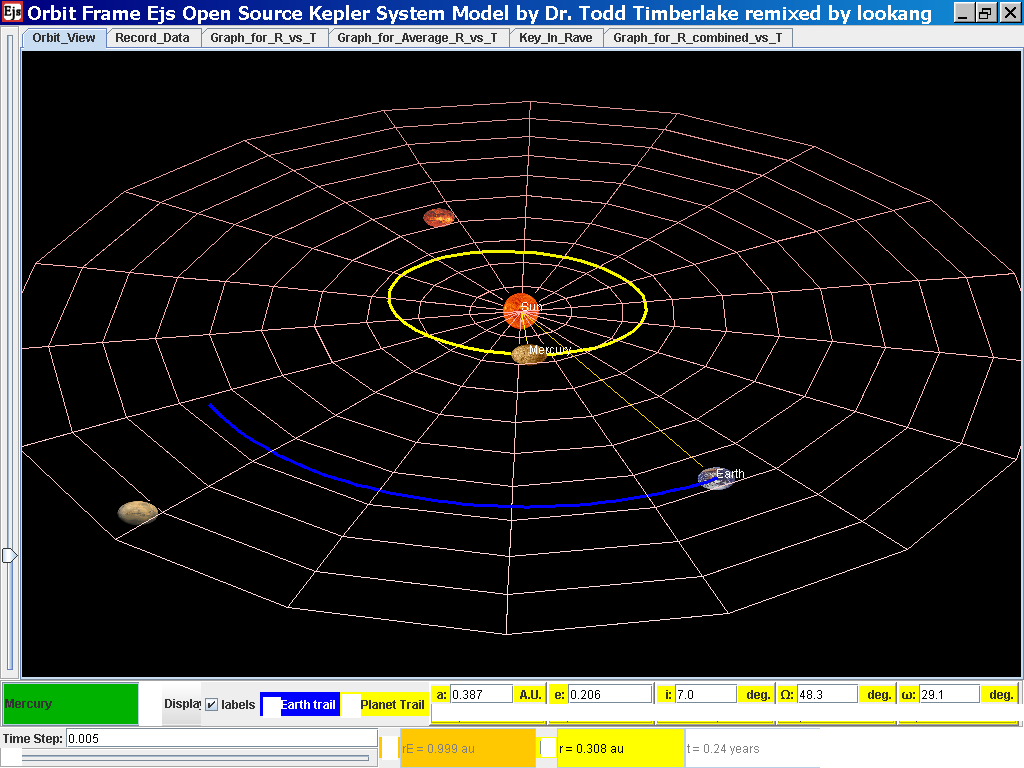
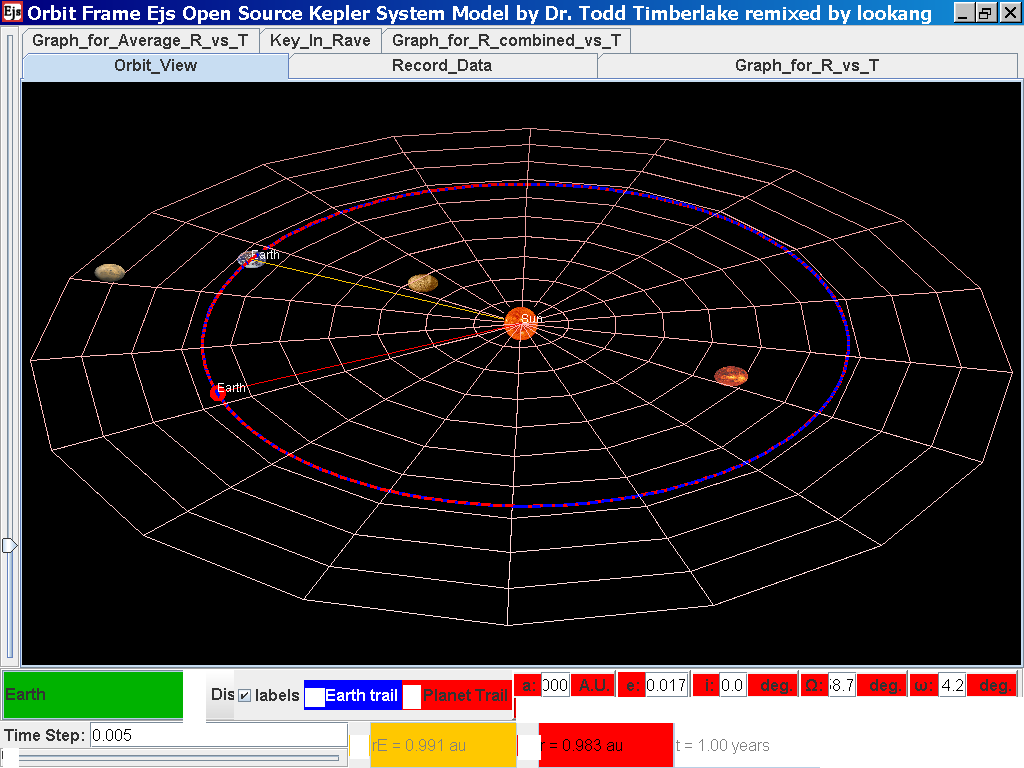
Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.

Click Pause to stop the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.

Click Step to fine tune your determination of period T, say t =0.24 years

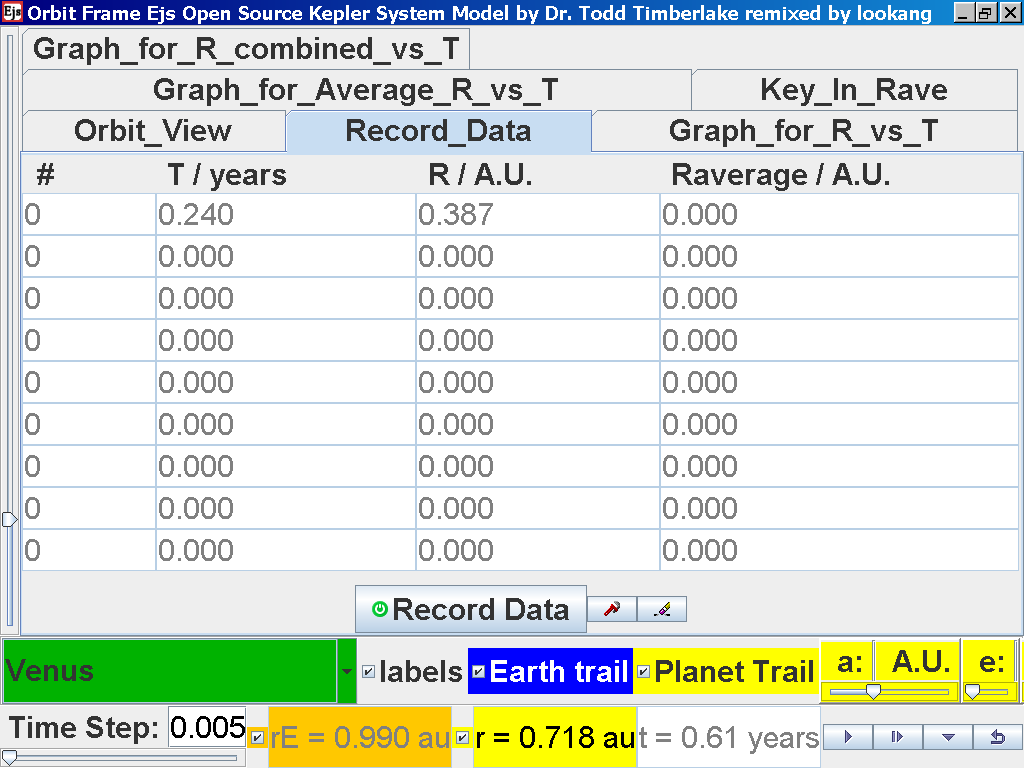
Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.

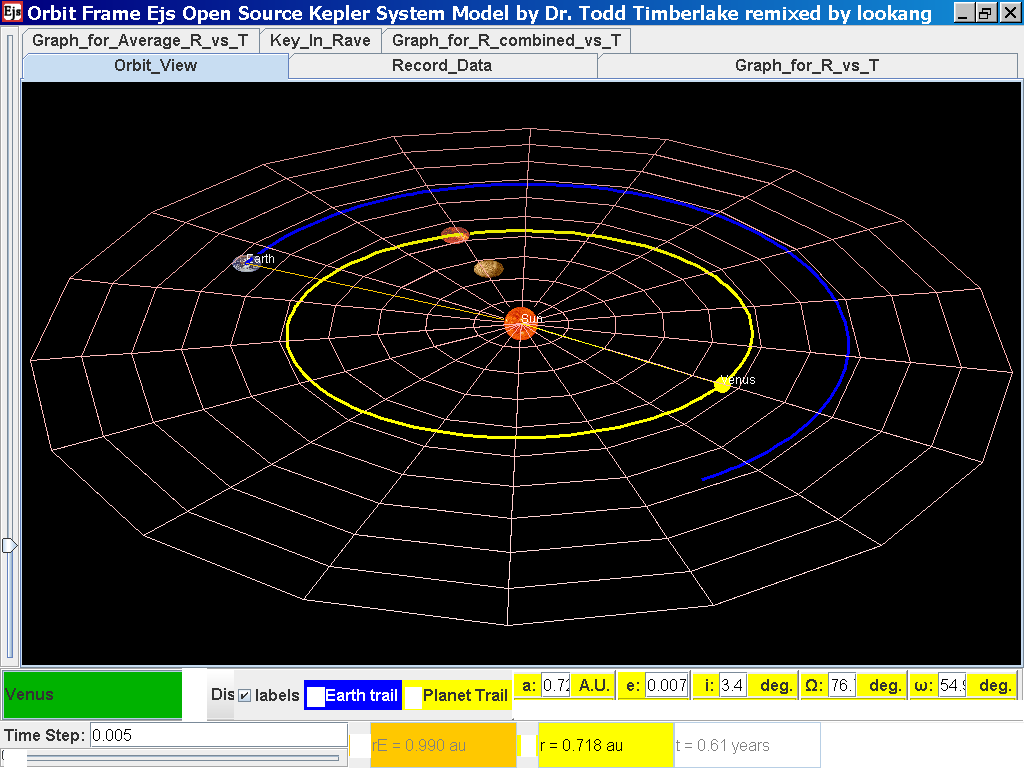
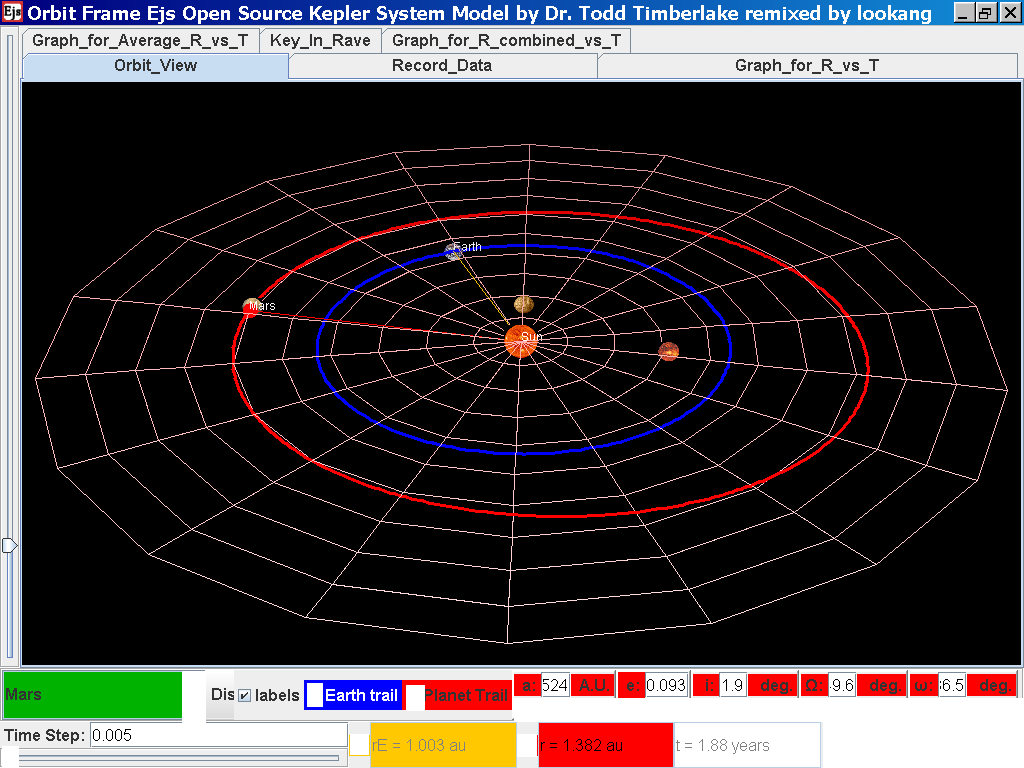
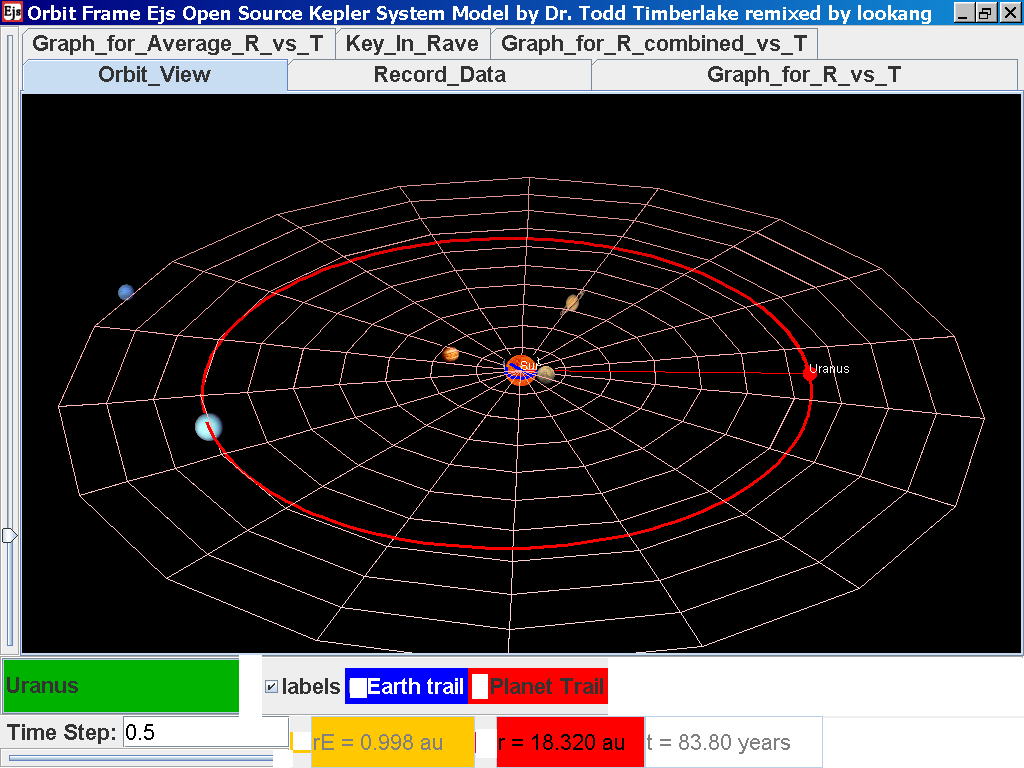
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle.

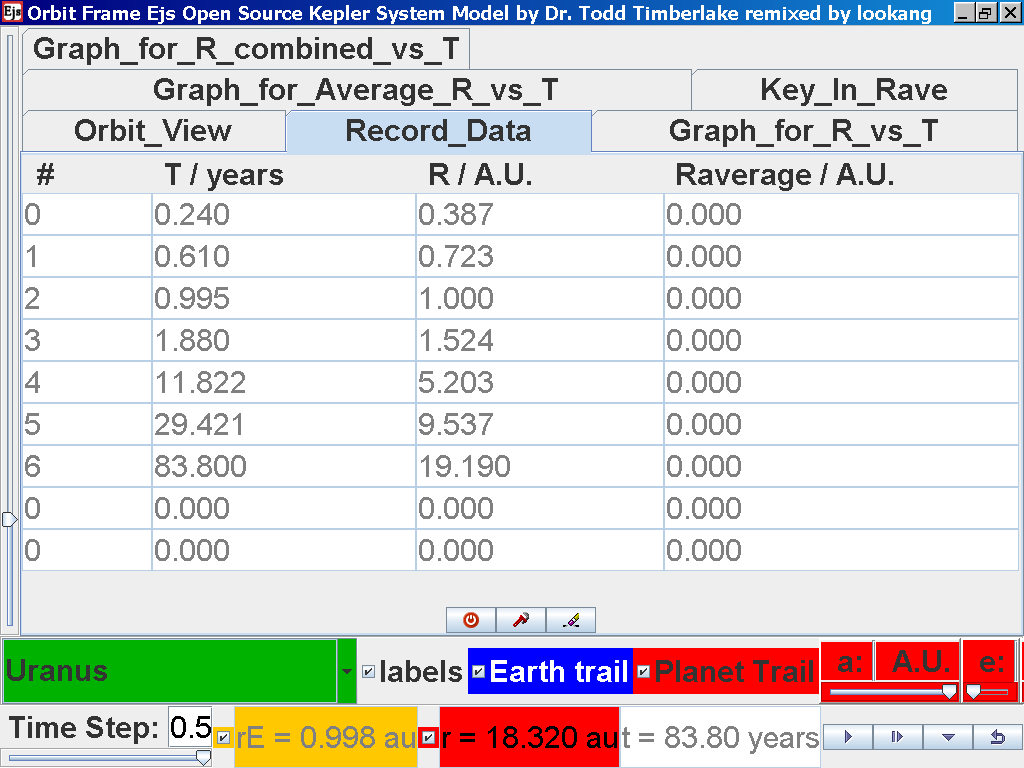
Click again on the next tab Record_Data and select Record_Data.

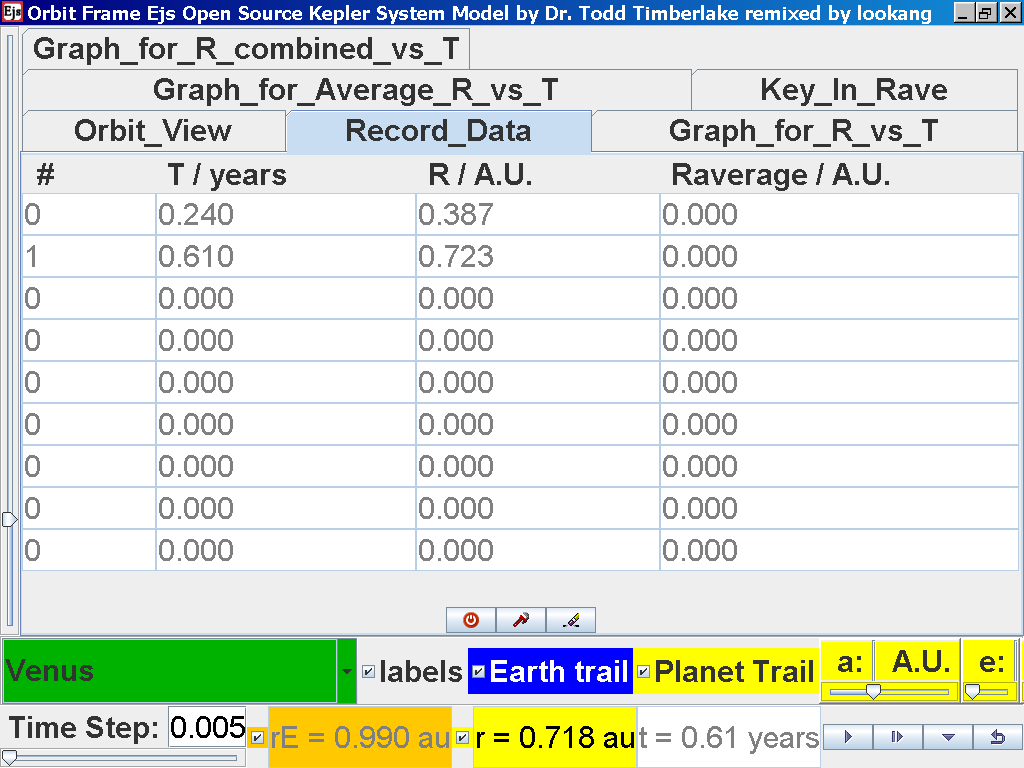
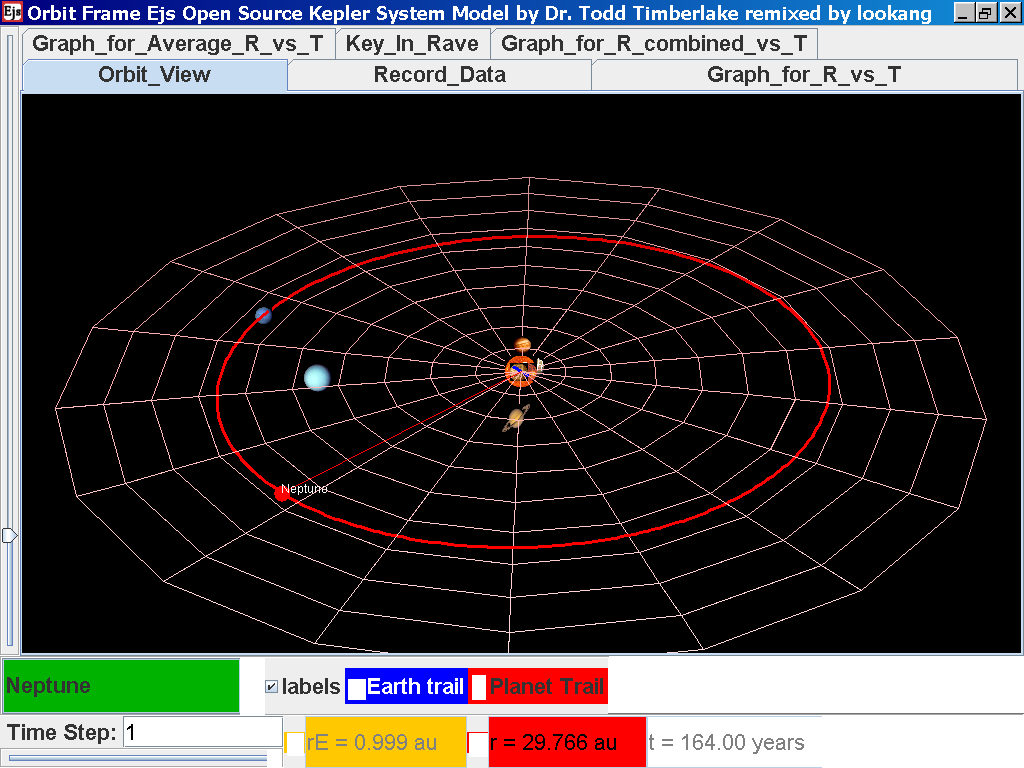
Repeat the above steps for the rest of the planets i.e. Earth, Mars, Jupiter, Saturn, Uranus, Neptune and Pluto. (Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle. )

Click again on the next tab Record_Data and select Record_Data.

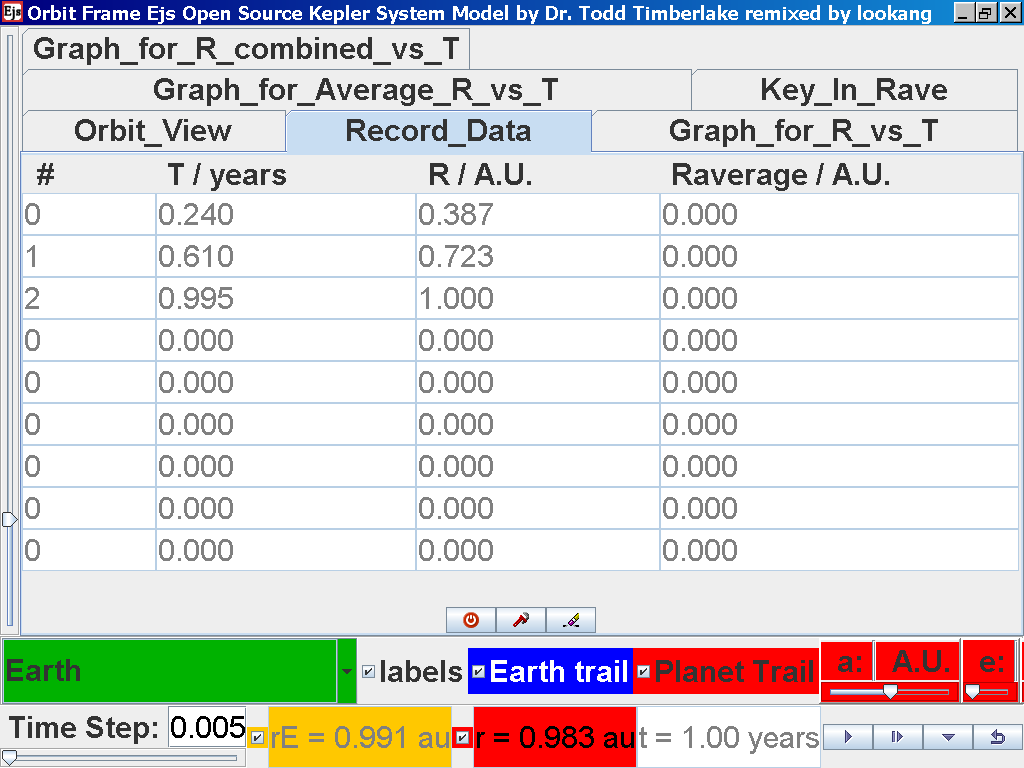
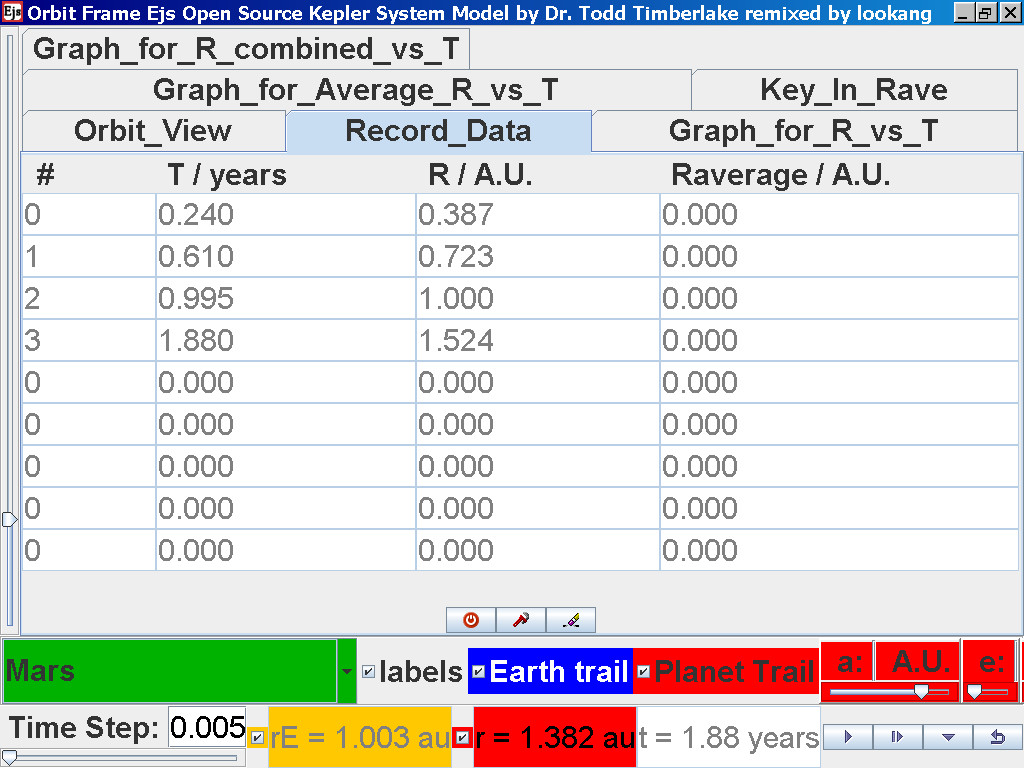
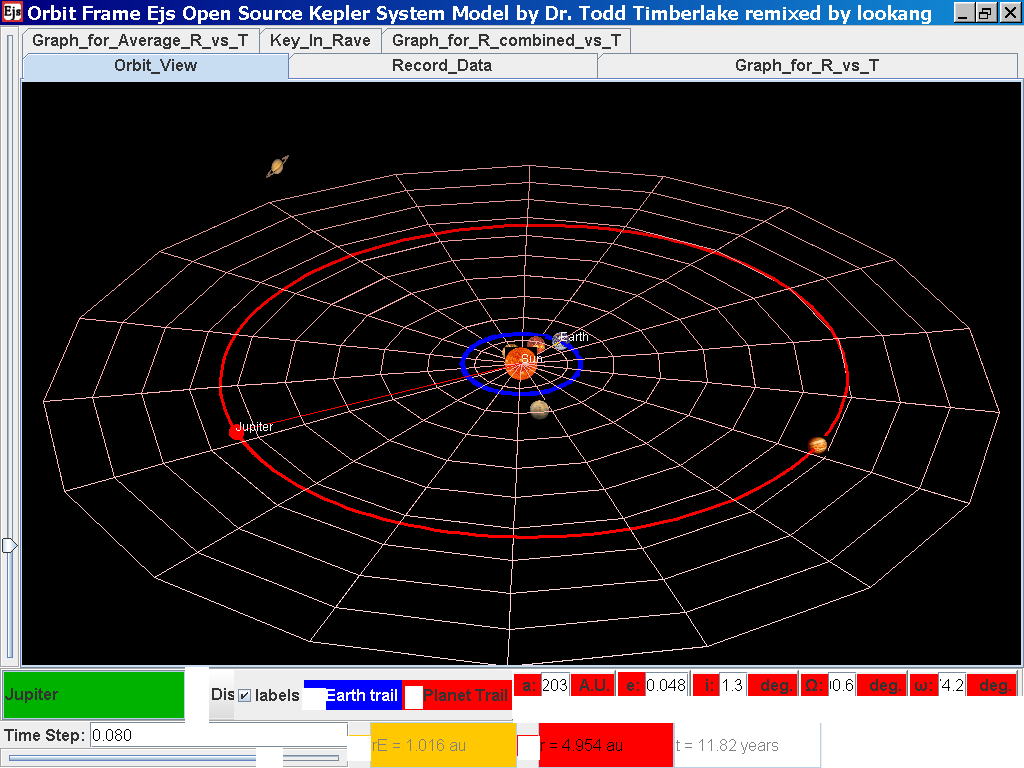
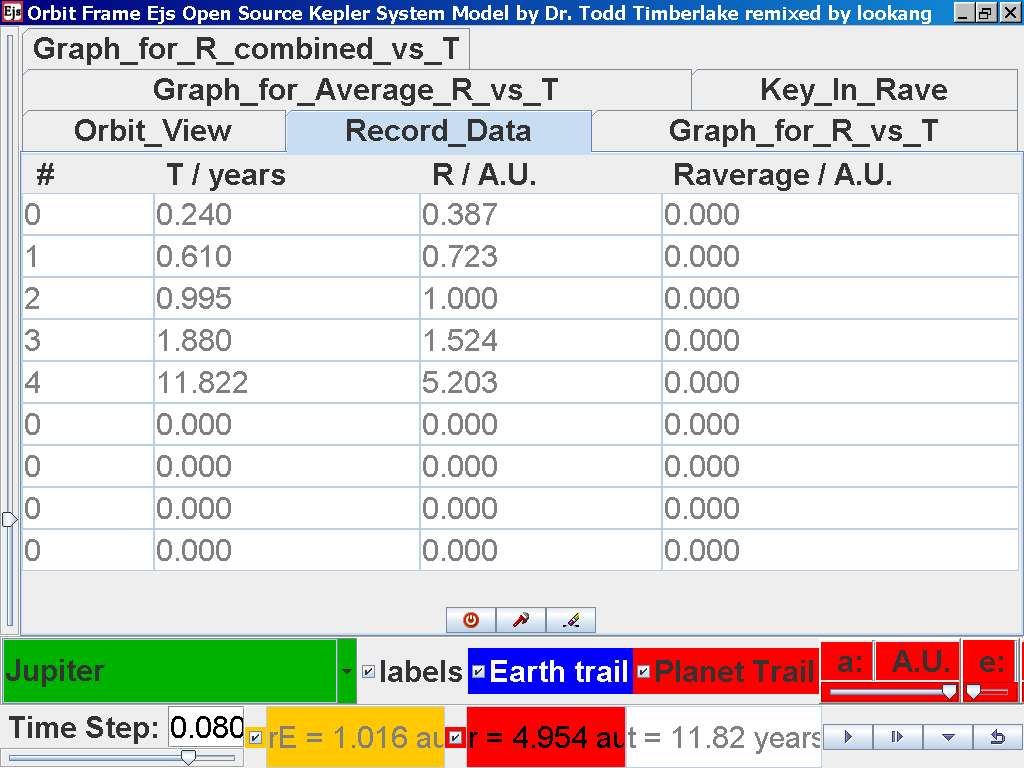
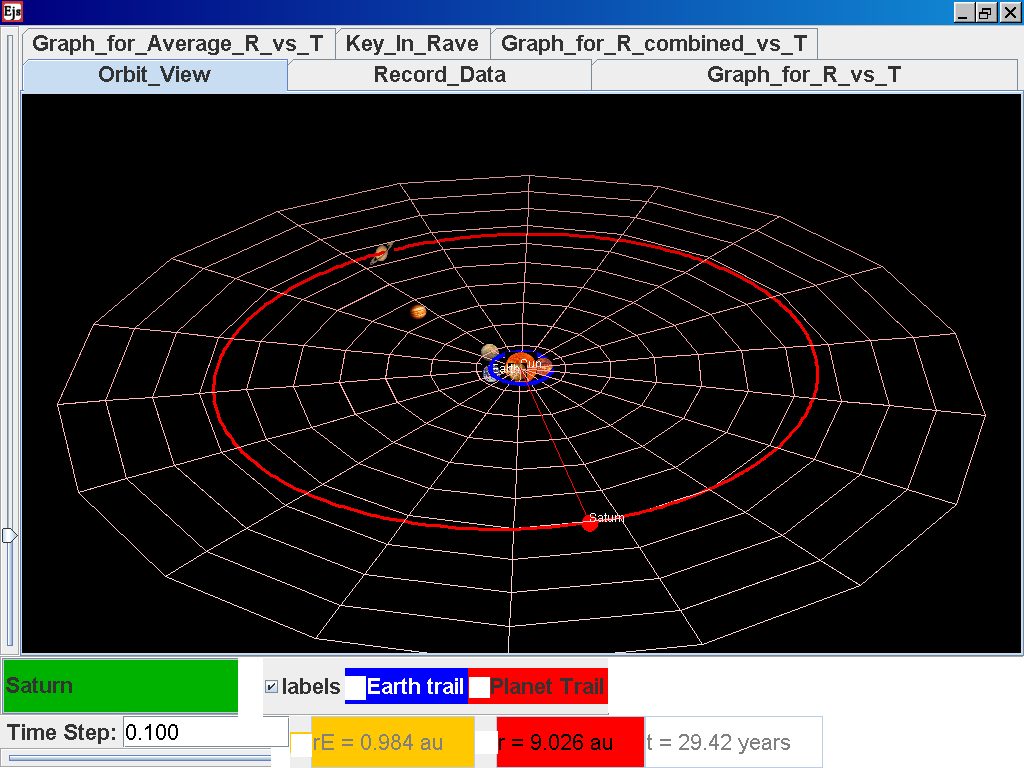
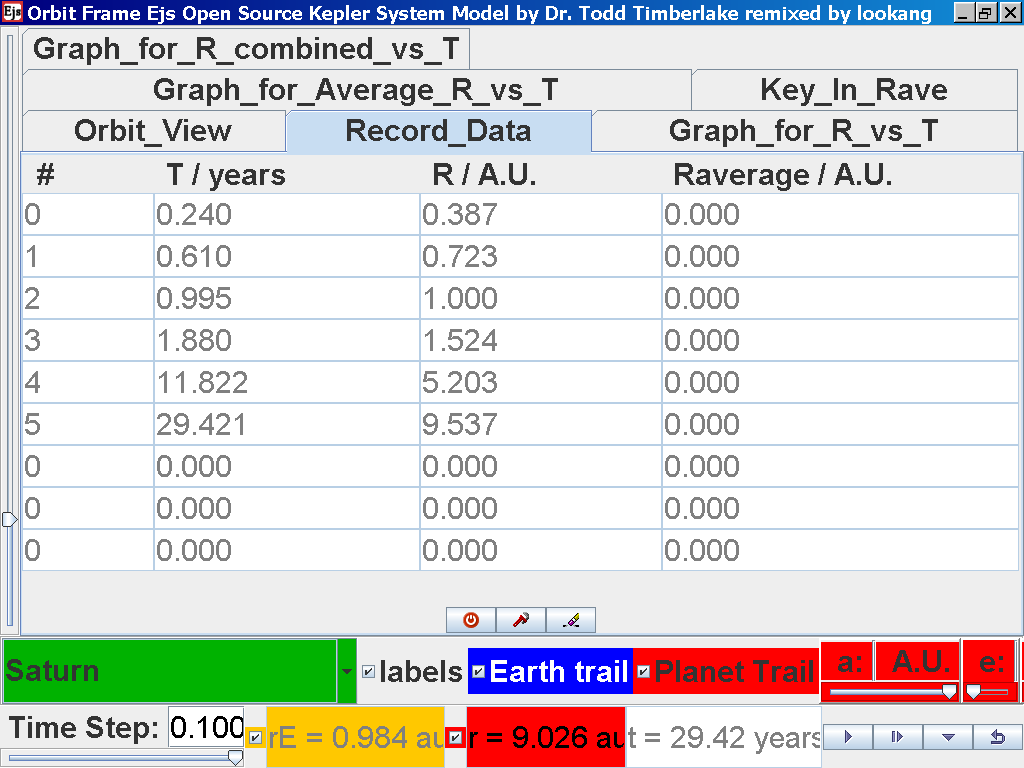
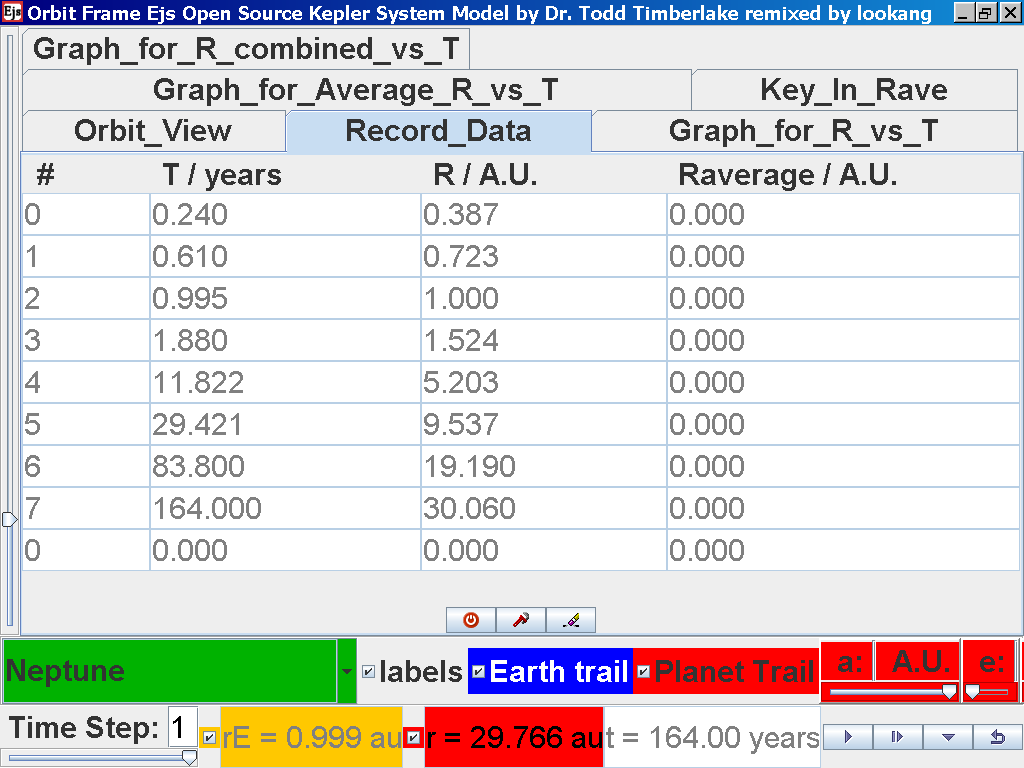
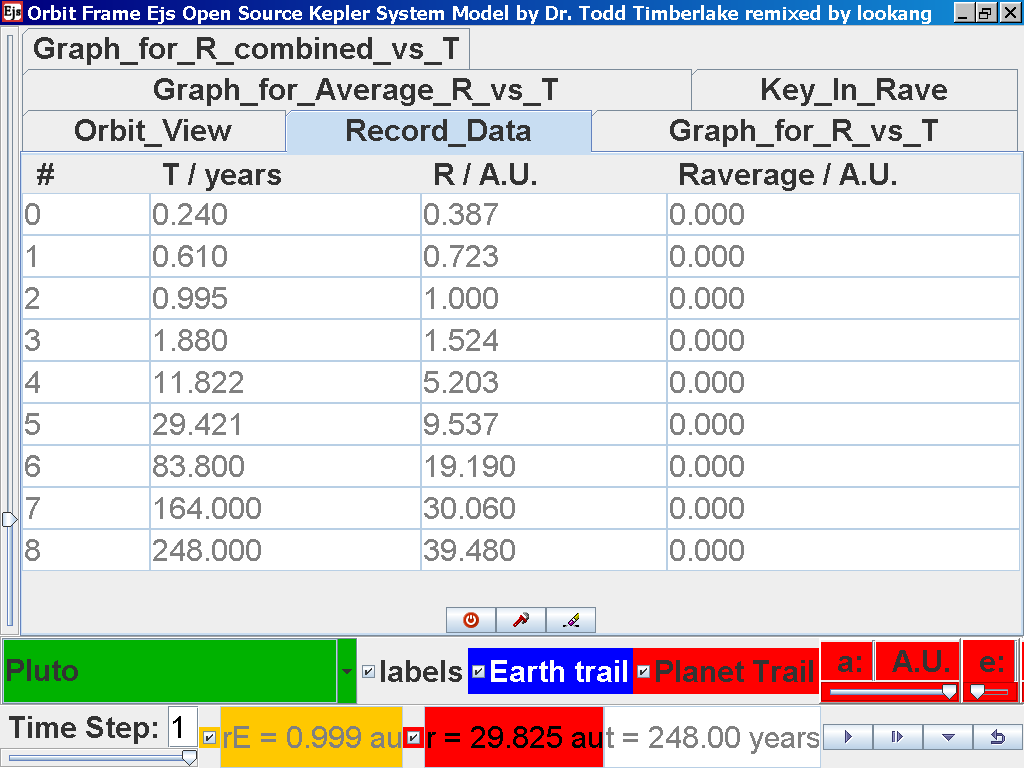
Notice all the data on the actual T /years recorded by you are slightly different compared to the mean radius of orbits R has units of A.U. (astronomical units) where by 1 A.U. = mean distance of Earth to Sun.

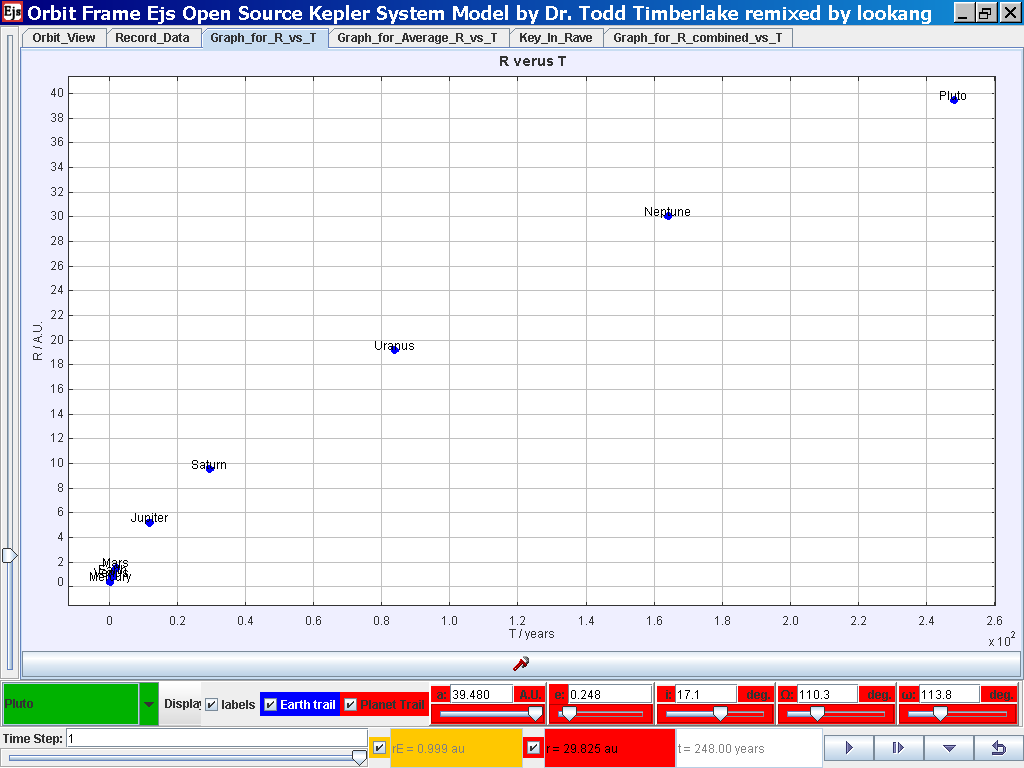
Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.

Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner

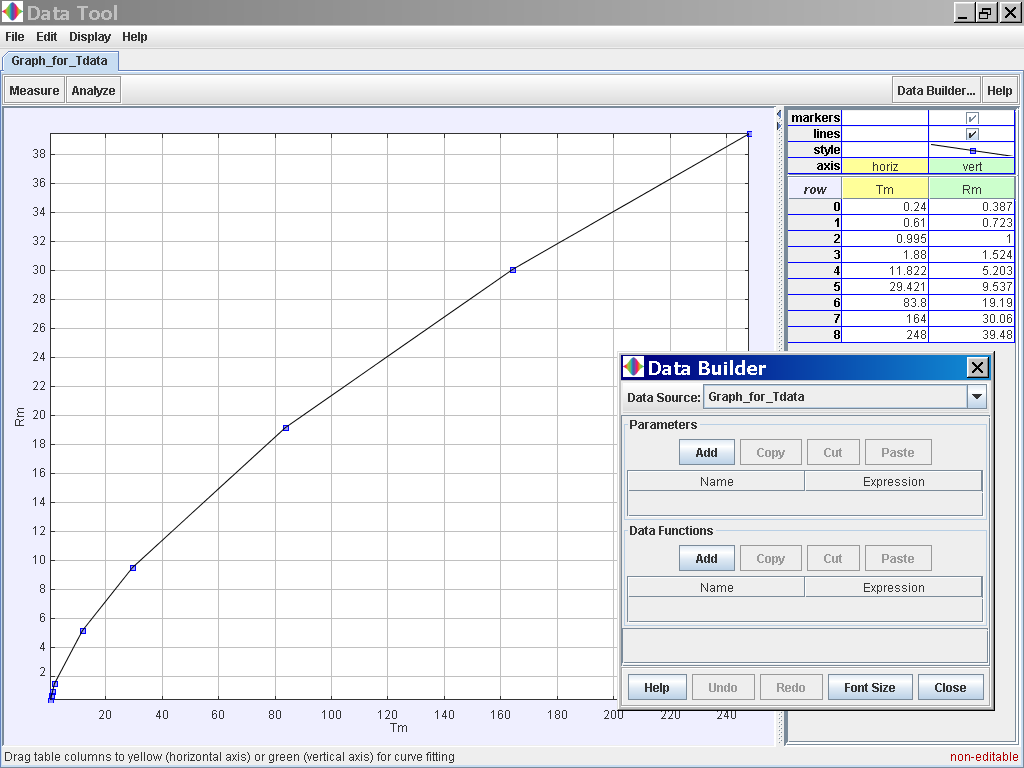
Click on the Data Function Add button to add your own functions such as T2 for T_mean² and R3 for r_mean³.

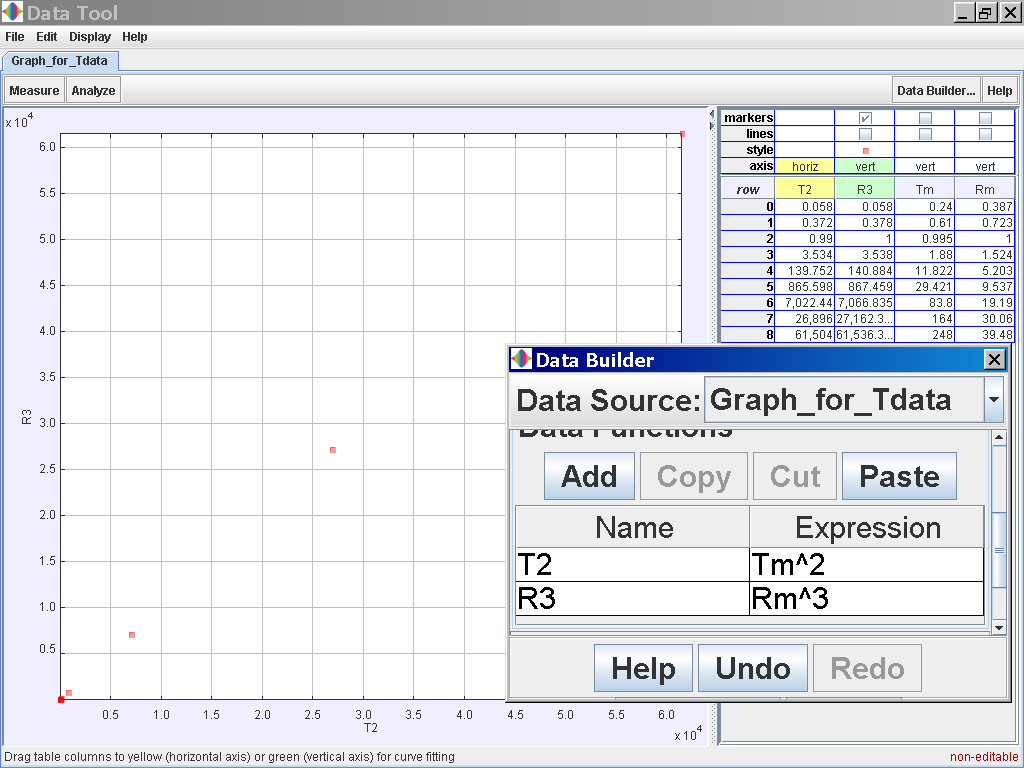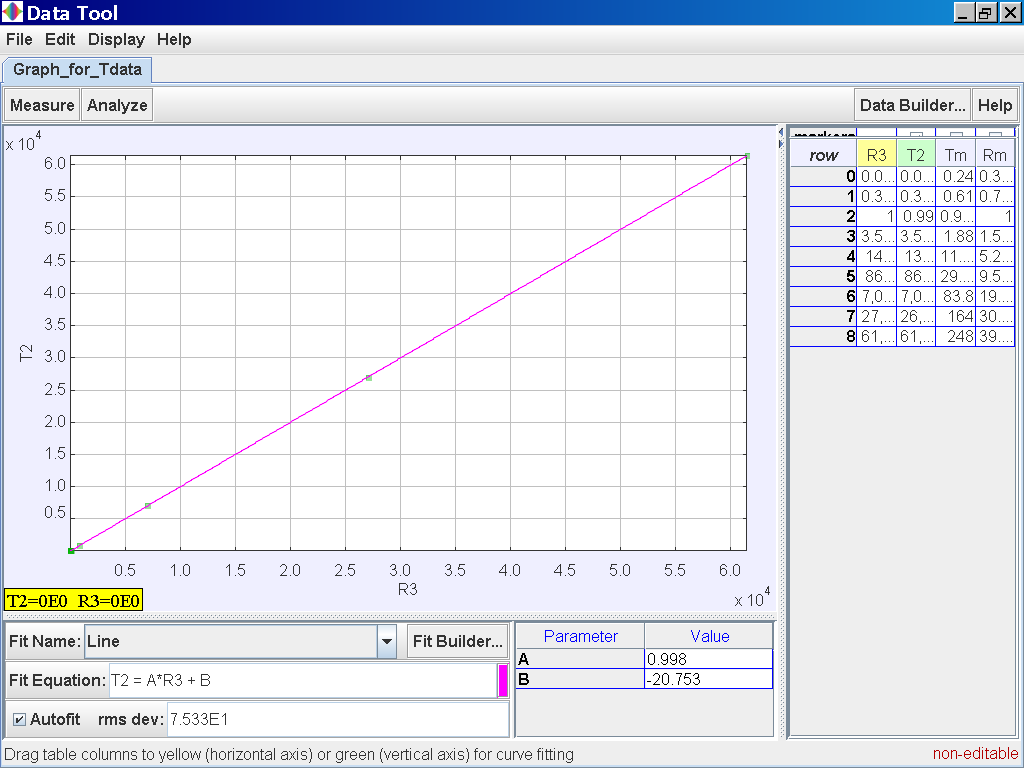
Click on the Analyse button on the top left corner and select the Linear Fit Option of which the data of T² and R³ is related by the following line fit
T² = 0.998 R³ -20.753 which suggests T² α r³

Alternatively, you can also try to plot log (T) versus log (R)

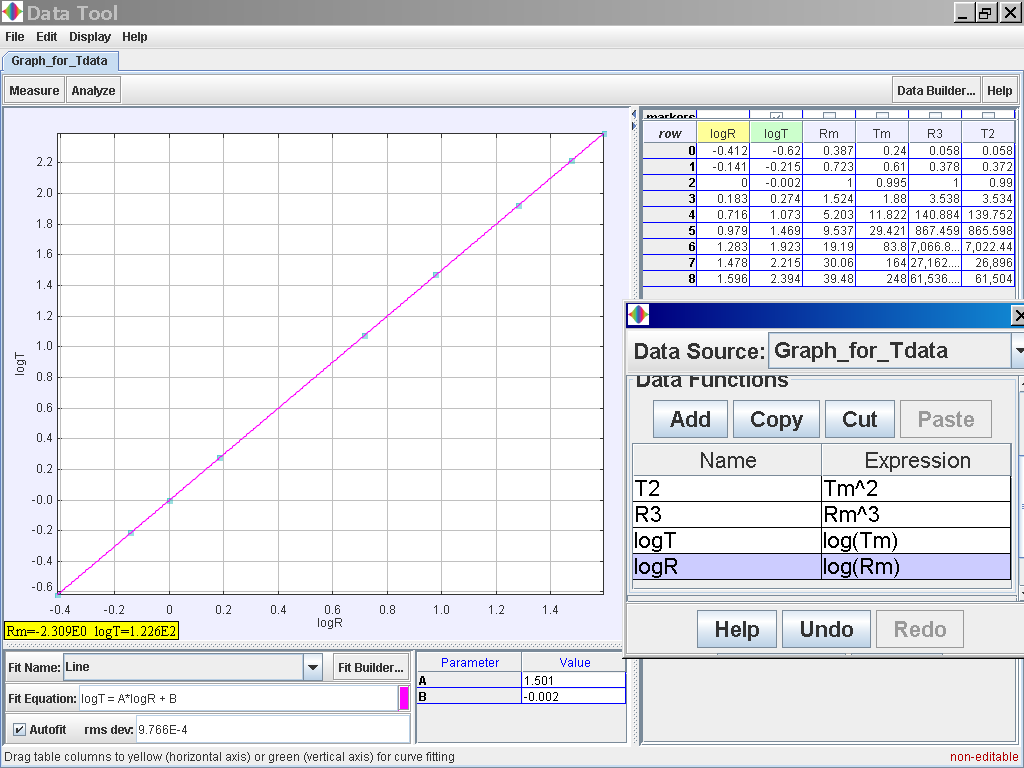
Notice that log (T) = 1.501 log (R) -0.002 which suggests the relationship of T α r^1.5 or simply T² α r³

7.5.1.4 YouTube

https://youtu.be/jt88koyZQuw Discovering Kepler 3rd System by inquiry collect data like scientists

7.5.1.5 Java simulation for the full inquiry described above

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_KeplerSystem3rdLaw09.jar

7.5.1.6 Model, you can record down the time for each planet's one revolution to determine if T² α r³is valid

Translations

Code	Language		Translator	Run

Credits

lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); Todd TimberLake

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity09/gravity09_Simulation.xhtml

Briefing Doc: 🪐Kepler's Third Law and Interactive Learning

Main Themes:

Kepler's Third Law: The primary focus of these sources is Kepler's Third Law of planetary motion, which states that the square of the period of an object in a circular orbit is directly proportional to the cube of the radius of its orbit. This is represented mathematically as T² α r³.
Interactive Learning: The sources emphasize the use of interactive simulations and online tools for understanding Kepler's Third Law. They provide step-by-step instructions on how to utilize these resources to collect data, analyze trends, and ultimately derive Kepler's Third Law through inquiry-based learning.

Most Important Ideas/Facts:

Derivation of Kepler's Third Law: The sources explain that Kepler's Third Law can be derived from Newton's Second Law applied to circular motion, where the gravitational force acts as the centripetal force. This is illustrated through the equation:

"G m M / r² = m r ω² = m r ( 2 π / T )² can be simplified to an equation involving T and r: T² = 4 π² G M / r³"

Applicability of Kepler's Third Law: The sources explicitly state that Kepler's Third Law is only applicable to objects in a circular orbit where the sole force acting on the object is the gravitational force acting as the centripetal force.

"The Kepler’s Third Law is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it to act as its centripetal force."

Interactive Simulation: The sources provide links to a JavaScript HTML5 WebGL Applet Simulation Model that allows users to visually observe and manipulate planetary orbits. Through this interactive model, users can collect data on the orbital period and radius of different planets in our solar system.

"Model, you can record down the time for each planet's one revolution to determine if T² α r³ is valid"

Quotes:

"This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit is directly proportional to the cube of the radius of its orbit."
"The Kepler’s Third Law T² α r³ is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it and thus it acts as the centripetal force."
"Complete ICT inquiry worksheet 2 to build your conceptual understanding on the Kepler’s Third Law."

Key Takeaways:

The sources present a compelling argument for the effectiveness of interactive simulations in teaching complex scientific concepts like Kepler's Third Law. By providing students with hands-on experience in collecting and analyzing data, these tools encourage a deeper understanding of the underlying principles.

Kepler's Third Law Study Guide

Short-Answer Questions

Explain the relationship between the gravitational force acting on a satellite in orbit and the centripetal force.
State Kepler's Third Law in words and provide its mathematical formula.
What is the significance of the constant of proportionality in Kepler's Third Law?
Why is Kepler's Third Law only applicable to objects in circular orbits?
How does the period of an object's orbit change if its orbital radius is doubled?
Describe how you could use the provided simulation to verify Kepler's Third Law.
What is an astronomical unit (A.U.) and how is it relevant to Kepler's Third Law?
What are some limitations of using a computer simulation to study Kepler's Third Law?
Besides the simulation mentioned, what other methods could be used to investigate Kepler's Third Law?
Explain how understanding Kepler's Third Law is relevant to modern space exploration.

Short-Answer Answer Key

The gravitational force acting on a satellite in orbit is the force responsible for providing the necessary centripetal force to maintain the satellite's circular motion. The gravitational force constantly pulls the satellite towards the center of the orbit, preventing it from moving in a straight line.
Kepler's Third Law states that the square of the period of an object in circular orbit is directly proportional to the cube of the radius of its orbit. Mathematically, it is expressed as T² ∝ r³, where T is the period and r is the orbital radius.
The constant of proportionality in Kepler's Third Law relates the square of the period to the cube of the radius. This constant depends on the mass of the central body around which the object is orbiting. For orbits around the Sun, the constant is 4π²/GM, where G is the gravitational constant and M is the mass of the Sun.
Kepler's Third Law is only applicable to objects in circular orbits because the derivation relies on the assumption that the gravitational force acts as the sole centripetal force. In elliptical orbits, the gravitational force is not always directed towards the center of the ellipse, leading to more complex relationships between period and radius.
According to Kepler's Third Law (T² ∝ r³), if the orbital radius (r) is doubled, the period (T) would increase by a factor of 2√2. This is because the square of the period is proportional to the cube of the radius.
The simulation can be used to verify Kepler's Third Law by recording the orbital periods (T) and mean radii (r) of different planets. By plotting T² against r³, a linear relationship should be observed, confirming the proportionality stated in the law.
An astronomical unit (A.U.) is a unit of length equal to the average distance between the Earth and the Sun. It is relevant to Kepler's Third Law because it provides a convenient scale for measuring orbital radii within our solar system.
Some limitations of using a computer simulation to study Kepler's Third Law include the inherent simplifications and assumptions made in the model, potential inaccuracies in the simulation's calculations, and the inability to account for all real-world factors influencing orbital motion.
Other methods to investigate Kepler's Third Law include: observing and analyzing real astronomical data of planets and moons, conducting experiments with controlled objects in a laboratory setting, and developing mathematical models based on Newton's Law of Universal Gravitation.
Understanding Kepler's Third Law is crucial for space exploration because it allows us to predict the orbital paths and periods of spacecraft. This knowledge is essential for planning missions, calculating fuel requirements, and designing trajectories for interplanetary travel and satellite deployments.

Essay Questions

Derive Kepler's Third Law mathematically, starting from Newton's Law of Universal Gravitation and the concept of centripetal force. Clearly explain each step in your derivation.
Compare and contrast Kepler's Third Law with his other two laws of planetary motion. Discuss their individual significance and how they contribute to our understanding of celestial mechanics.
Analyze the limitations of Kepler's Laws. To what extent do they accurately describe the motion of celestial objects? Discuss factors that can cause deviations from Keplerian orbits.
Explain how technology has advanced our ability to study and verify Kepler's Laws since their initial discovery. Describe specific instruments and techniques used by modern astronomers.
Discuss the influence of Kepler's Laws on the development of scientific thought. How did his work challenge existing paradigms and pave the way for future discoveries in physics and astronomy?

Glossary of Key Terms

Centripetal Force: The force directed towards the center of a circular path, required to keep an object moving in that path.

Circular Orbit: An orbit where an object follows a circular path around a central body.

Gravitational Force: The attractive force between any two objects with mass.

Kepler's Third Law: The law stating that the square of the period of an object's orbit is proportional to the cube of its orbital radius.

Newton's Law of Universal Gravitation: The law stating that every object attracts every other object with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.

Orbital Radius: The average distance between the center of a celestial object and the center of the object it is orbiting.

Period: The time it takes for an object to complete one full orbit.

Proportionality: A relationship between two quantities where their ratio is constant.

Satellite: An object that orbits a larger celestial body, such as a planet or a star.

Apps

Cover art https://play.google.com/store/apps/details?id=com.ionicframework.gravity091app597842

Kepler’s Third Law

It was stated that the gravitational force acting on a satellite in orbit is the centripetal force to keep it in circular motion.

i.e.              ΣF = mrω2
            G m M r 2 = m r ω 2

recalling in circular motion,  ω = 2 πT
Hence,      G m M r 2 = m r ω 2 = m r( 2 π T ) 2

can be simplified to an equation involving T and r

T 2 = 4 π 2 G M r 3

This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit (i.e. the gravitational force acts as the centripetal force) is directly proportional to the cube of the radius of its orbit. T2 α r3

Note:
• The Kepler’s Third Law is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it to act as its centripetal force.

Complete ICT inquiry worksheet 2 to build your conceptual understanding on the Kepler’s Third Law.

This series of screenshot serves to guide your inquiry

Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.

Click Pause the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.

Click Step to fine tune your determination of period T, say t =0.24 years

Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle.

again click on the next tab Record_Data and select Record_Data.

Now the steps need to be repeated for the rest of the planets. Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle.

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Mars. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Jupiter. Play the simulation for one complete cycle and increase the time step = 0.08 years reduces the time needed to wait for one cycle.

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Saturn. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Uranus. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Neptune. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

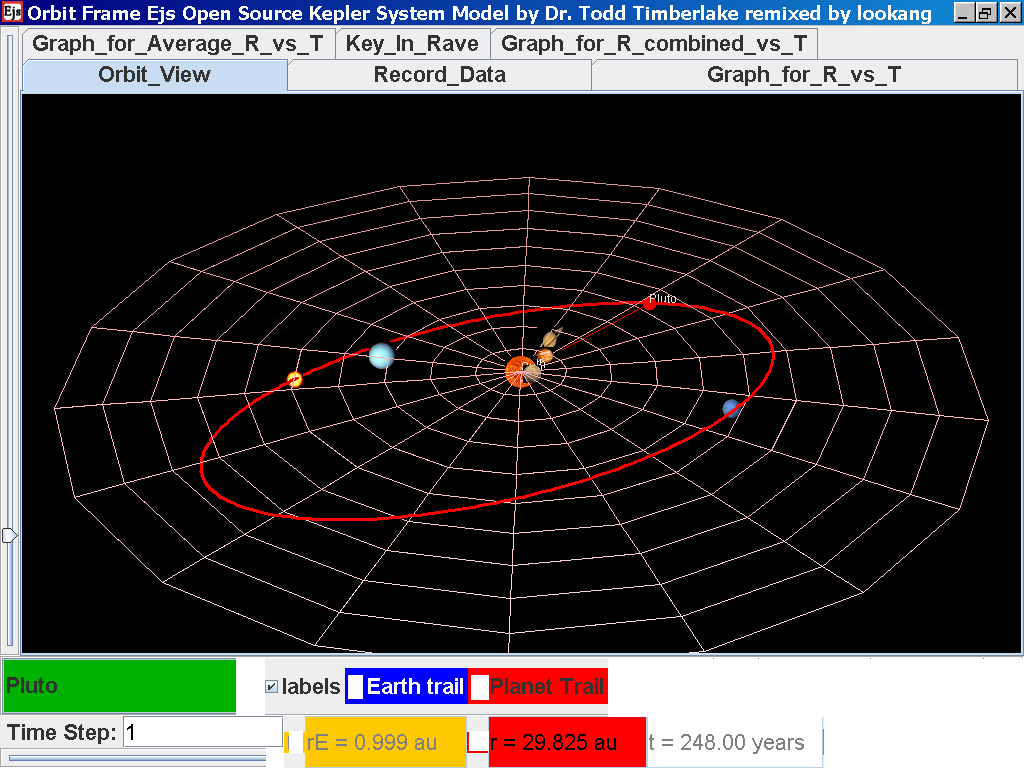
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Pluto. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Notice all the data on the actual T /years recorded by you is slightly different and the mean radius of orbits R / A.U. astronomical units which 1 A.U. = mean distance of Earth to Sun.

Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.

Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner

Click on the Data Function Add button to add your own functions such as T2 for Tmean2 and r3 for rmean3.
Click on the Analyse button on the top left corner and select the Linear Fit option of which the data of T2and R3 is related by the following line fit
T2 = 0.998 R3 -20.753 which suggests T2 α r3

Alternative activity, you can also try to log (T) versus log (R)
notice again log (T) = 1.501 log (R) -0.002 which suggests the same relationship of T α r1.5 or simply T2α r3

Versions

Worksheets

Kepler's Third Law FAQ

What is Kepler's Third Law?

Kepler's Third Law states that the square of the period of an object in a circular orbit is directly proportional to the cube of the radius of its orbit. This can be represented mathematically as:

T2 ∝ r3

where:

T is the period of the orbit (the time it takes for the object to complete one full revolution)
r is the radius of the orbit

What does "directly proportional" mean in the context of Kepler's Third Law?

Direct proportionality means that as one quantity increases, the other quantity increases at a constant rate. In the case of Kepler's Third Law, if you double the radius of the orbit, the square of the orbital period will increase by a factor of eight (2 cubed).

Does Kepler's Third Law apply to all objects in orbit?

No, Kepler's Third Law, as described here, specifically applies to objects in circular orbits where the gravitational force is the only force acting on the object. This means it acts as the centripetal force, keeping the object moving in a circle.

Can Kepler's Third Law be used to calculate the period or radius of an orbit?

Yes, if you know the mass of the central object (like the Sun) and either the period or the radius of the orbit, you can use Kepler's Third Law to calculate the other unknown value.

How is Kepler's Third Law derived?

Kepler's Third Law can be derived from Newton's Law of Universal Gravitation and the equations for circular motion. By setting the gravitational force equal to the centripetal force required for circular motion, and substituting the appropriate expressions, you arrive at the mathematical relationship described by Kepler's Third Law.

How can I investigate Kepler's Third Law using a simulation?

The source provided mentions a JavaScript HTML5 WebGL Applet Simulation Model that allows you to collect data on the orbital periods and radii of planets in our solar system. You can use this simulation to record data for each planet and then plot the data to verify that the relationship between T2 and r3 is indeed linear, confirming Kepler's Third Law.

What are Astronomical Units (AU)?

An Astronomical Unit (AU) is a unit of length commonly used in astronomy. It is defined as the average distance between the Earth and the Sun. 1 AU is approximately equal to 149.6 million kilometers.

Where can I find more information and resources on Kepler's Third Law?

The source provided includes links to YouTube videos, Java simulations, and other online resources that can help you further understand Kepler's Third Law. Additionally, searching for "Kepler's Third Law" on educational websites or physics textbooks will yield a wealth of information.

5 1 1 1 1 1 1 1 1 1 1 Rating 5.00 (3 Votes)

Details: Written by Loo Kang Wee; Parent Category: 02 Newtonian Mechanics; Category: 08 Gravity; Published: 24 September 2015; Created: 24 September 2015; Last Updated: 28 December 2024; Hits: 13412