
About
For Teachers
- Modelling Skydiving with Parachute Opening_parameterized1491.jpg
- Modelling Skydiving with Parachute Opening_parameterized0000.jpg
- ModellingSkydivingwithParachuteOpening_forLookang.docx
Credits
Author: Tan Kim Kia
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it. | This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Doc: 🪂Skydiving with Parachute Opening - Tracker Modeling
This briefing document reviews the key themes and findings from a blog post and accompanying Tracker software files exploring skydiving physics using the Tracker software. The author, Tan Kim Kia, presents two models simulating parachute opening and analyzes their results.
Main Themes:
- Parachute Opening Dynamics: The document focuses on comparing two distinct models for parachute opening – gradual opening (Model A) and instantaneous opening (Model B) – and their impact on the skydiver's descent.
- Realistic Modeling: The author emphasizes the importance of developing models that accurately reflect real-world physics, considering factors like air density, drag coefficients, and the time taken for parachute deployment.
- Challenging Assumptions: The author critically evaluates the assumptions made in a Singapore O Level Physics exam question, arguing for a more realistic approach based on real-world parachute deployment dynamics.
Key Ideas and Facts:
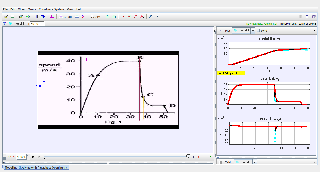
- Model A (Gradual Opening): This model utilizes a parameterized force equation (Fy) that accounts for varying drag forces as the parachute opens over a specific duration (T). The velocity-time graph for this model shows a smoother deceleration curve.
- Equation: Fy = if(t<35,m*g-A_h*0.5*d*Cd*vy^2,if(t<55,m*g-0.5*d*Cd2*A_p*vy^2,if(vy>0,-m*g,0)))
- Model B (Instantaneous Opening): This model assumes the parachute opens fully and immediately (T=0). The velocity-time graph exhibits a sharp, almost instantaneous drop in velocity.
- Equation: Fy = if(t<35,m*g-A_h*0.5*d*Cd*vy^2,if(t<35+T,m*g-0.5*d*Cd2*(A_h+(t-35)/T*A_p)*vy^2,if(t<55,m*g-0.5*d*Cd2*(A_h+A_p)*vy^2,if(vy>0,-m*g,0))))
- Deceleration Comparison: Model A results in a deceleration of 3.1g, deemed realistic, while Model B yields a much higher deceleration of 17g, considered unrealistic and potentially harmful.
- Real-World Evidence: A Discovery Education Channel video cited by the author suggests parachutes typically take 2-3 seconds to fully deploy, supporting the validity of Model A's gradual opening approach.
Significant Quotes:
- "Model A’s deceleration is 3.1g, which is realistically small, and therefore, it is believable the correct answer."
- "Model B has a deceleration of 17g, which is unrealistic big and likely to cause hurt on the parachutist, which is the examiners answer of B."
- "I think it is a bad idea to open the parachute immediate while the parachutist is falling at 40 m/s."
Teaching Ideas:
The author encourages readers to use the provided Tracker files to experiment with different parameters and observe the impact on the velocity and acceleration graphs. This hands-on approach can deepen understanding of skydiving physics and promote critical thinking about modeling choices.
Skydiving with Parachute Opening: A Tracker Modelling Study Guide
Short Answer Questions:
- What are the two skydiving models (A and B) presented in the article, and what is the key difference between them?
- What is the significance of the variable "T" in both Model A and Model B? How does its manipulation affect the simulation?
- The author argues that Model A's deceleration is more realistic. What is the basis for this claim, and why is Model B's deceleration considered unrealistic?
- What real-world evidence does the author cite to support the validity of Model A over Model B?
- Describe the purpose of the formula "Fy = if(t<35,m*g-A_h*0.5*d*Cd*vy^2,if(t<55,m*g-0.5*d*Cd2*A_p*vy^2,if(vy>0,-m*g,0)))" used in Model A.
- Explain the concept of drag force and its role in skydiving. How does the parachute affect the drag force experienced by the skydiver?
- What is the relationship between the surface area of the parachute and the deceleration experienced by the skydiver?
- Why is it important to consider the duration of parachute opening when modeling skydiving?
- What insights can be gained by comparing the velocity-time and acceleration-time graphs for Model A and Model B?
- The article mentions a Singapore O Level Physics question related to skydiving. What is the connection between the question and the discussion of the models?
Answer Key:
- Model A simulates a parachute opening slowly over a period of time (T), while Model B simulates the parachute opening fully and immediately (T=0). The key difference lies in the duration of parachute deployment.
- "T" represents the duration for parachute opening. In Model A, it dictates how slowly the parachute opens, while in Model B, it is set to zero, indicating instant opening. Manipulating "T" alters the rate of change in drag force and thus the deceleration experienced.
- Model A's deceleration of 3.1g is considered realistic as it aligns with the survivable limits of human tolerance for G-forces. Model B's deceleration of 17g is unrealistic and dangerous, potentially causing severe injury to the skydiver.
- The author references a Discovery Education Channel video showing parachutes taking 2-3 seconds to open fully in real-life scenarios, supporting the gradual opening represented by Model A.
- This formula calculates the net force (Fy) acting on the skydiver at any given time (t). It considers the forces of gravity, air resistance (drag) based on velocity (vy), and the changing surface area of the parachute as it opens.
- Drag force is air resistance opposing the motion of a falling object. It increases with velocity and surface area. The parachute drastically increases the surface area, significantly increasing drag force, and slowing the skydiver's descent.
- A larger parachute surface area leads to a greater drag force and consequently, a higher deceleration. This is why parachutes are designed with a large surface area to ensure a safe landing speed.
- The duration of parachute opening directly influences the rate of deceleration. A rapid opening creates a sudden and intense spike in G-forces, while a gradual opening allows for a smoother, more controlled deceleration.
- Comparing the graphs reveals the difference in deceleration profiles between the models. Model A shows a gradual decrease in velocity and a more realistic, lower peak in acceleration compared to the abrupt change and high peak in Model B.
- The physics question likely deals with the concepts of forces, motion, and air resistance in the context of skydiving, challenging students to apply their understanding to a real-world scenario. The models discussed in the article provide a framework for understanding the physics involved in the question.
Essay Questions:
- Analyze the limitations of using simplified models like Model A and Model B to represent complex real-world phenomena like skydiving. What factors might these models not fully account for, and how could they be improved to provide a more accurate representation?
- Discuss the ethical implications of using computer simulations to model potentially dangerous activities like skydiving. What are the potential benefits and risks of relying on these simulations for training and research purposes?
- Explain the concept of terminal velocity and its relevance to skydiving. How does the deployment of the parachute affect the skydiver's terminal velocity, and why is this crucial for a safe landing?
- Using the provided formulas as a starting point, design a modified model that incorporates additional factors influencing the skydiver's descent, such as wind conditions, altitude, and parachute deployment mechanisms. Justify your chosen factors and explain how they would be incorporated into the model's equations.
- Compare and contrast the use of Tracker software for modeling skydiving with other potential methods, such as wind tunnel experiments or computational fluid dynamics simulations. Discuss the advantages and disadvantages of each approach in terms of cost, accuracy, and practical applications.
Glossary of Key Terms:
Tracker: A free video analysis and modeling tool used for physics education and research.
Model A: A Tracker model simulating a parachute opening gradually over time.
Model B: A Tracker model simulating an instantaneous parachute opening.
T: The variable representing the duration of parachute opening in the models.
Deceleration: The rate of decrease in velocity, experienced as a force opposite to the direction of motion.
g-force (g): A unit of acceleration equal to the acceleration due to gravity at the Earth's surface (approximately 9.8 m/s²).
Drag force: The force of air resistance that opposes the motion of an object through the air.
Surface area: The total area of the outer surface of an object, in this case, the parachute.
Velocity-time graph: A graph plotting the velocity of an object against time, showing how speed changes over time.
Acceleration-time graph: A graph plotting the acceleration of an object against time, showing changes in acceleration over time.
Terminal velocity: The constant speed that a freely falling object eventually reaches when the force of air resistance equals the force of gravity.
Reference:
http://tankimkia.blogspot.sg/2015/10/modelling-skydiving-with-tracker.html?spref=fb
https://drive.google.com/folderview?id=0Bw72rpuy2MMLRUFtM1c1VzM2Rk0&usp=sharing#
Modelling Skydiving with Tracker Software
Model A(Red): Parachute opens slowly over T seconds
Fy = if(t<35,m*g-A_h*0.5*d*Cd*vy^2,if(t<55,m*g-0.5*d*Cd2*A_p*vy^2,if(vy>0,-m*g,0)))
Model B(Blue): Parachute opens fully immediately T = 0
Fy = if(t<35,m*g-A_h*0.5*d*Cd*vy^2,if(t<35+T,m*g-0.5*d*Cd2*(A_h+(t-35)/T*A_p)*vy^2,if(t<55,m*g-0.5*d*Cd2*(A_h+A_p)*vy^2,if(vy>0,-m*g,0))))
Velocity-time graph for Model B:
Conclusion
Ideas for teaching and demonstration:
Skydiving with Parachute Opening: FAQ
1. What is the purpose of using Tracker software to model skydiving?
Tracker software allows us to visually and mathematically simulate the physics of skydiving. By inputting parameters like air density, drag coefficients, and parachute surface area, we can model different scenarios and analyze factors like velocity and acceleration during a skydive.
2. What are the key differences between Model A and Model B in the skydiving simulation?
Model A simulates a parachute that opens gradually over a period of time (T seconds), while Model B assumes an instantaneous full parachute opening (T=0). This difference leads to significant variations in the deceleration experienced by the skydiver.
3. Why is Model A considered more realistic than Model B?
Model A's gradual parachute opening results in a deceleration of around 3.1g, which is a safe and realistic value for human skydivers. In contrast, Model B's immediate opening generates a deceleration of 17g, a force that would likely cause severe injury.
4. How does real-world parachute deployment compare to the models?
Real-world parachutes typically take 2-3 seconds to fully open, aligning more closely with the gradual deployment in Model A. Opening a parachute instantly at high speeds is not practiced due to the extreme forces involved.
5. What parameters can be adjusted in the Tracker skydiving model?
Parameters like the mass of the skydiver, surface area of the human body and parachute, drag coefficients, air density, and parachute opening duration (T) can be adjusted to explore various scenarios and their effects on the skydive.
6. What insights can be gained by comparing velocity-time and acceleration-time graphs for the models?
These graphs help visualize the differences in descent speed and deceleration between the models. Model A exhibits a smoother transition in velocity and a lower peak acceleration compared to the abrupt changes in Model B.
7. How does the skydiving simulation relate to the Singapore O Level Physics question 5058/2010/P1 Q3?
Both the simulation and the exam question highlight the importance of understanding the physics involved in parachute opening and the potential dangers of rapid deceleration.
8. What are some teaching applications for the Tracker skydiving model?
Educators can use this model to demonstrate key physics concepts like air resistance, terminal velocity, and the relationship between force, mass, and acceleration. Students can manipulate parameters and observe the effects on the skydive, fostering a deeper understanding of the principles at play.
- Details
- Written by Kimkia
- Parent Category: 03 Motion & Forces
- Category: 02 Dynamics
- Hits: 13623




