About
Projectile Motion with System of Masses and Spring
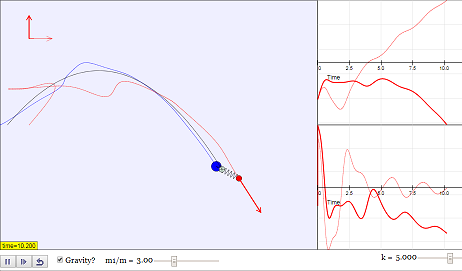
This is the simulation of the motion of two masses m and m1 situated at the ends of a spring of length L0 and negligible mass. The motion is restricted to two spatial dimensions, with the y-axis representing the vertical (if gravity is switched on).
We use Hooke's law for the spring force, and include a damping term that is proportional to the difference of the velocities of the masses on both ends of the spring. You can also choose for the spring to behave like a spring only when stretched, and have no effect when compressed (i.e. it is more like a string).
Applying Newton's Second Law yields a second-order ordinary differential equation, which we solve numerically in the simulation and visualise the results.
Activities
- Drag the red mass to impart an initial velocity, and see how the system evolves.
- Observe what happens when you do the same, but with gravity switched on.
- Try changing the relative mass of the blue ball, and notice how the centre of gravity shifts.
- Try varying the spring constant and/or the damping coefficient while the simulation runs.
- Also try activating the "string-like" mode such that the elastic force only occurs in the stretched state and not in the compressed state.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits


 Wolfgang Christian; Francisco Esquembre; Zhiming Darren TAN
Wolfgang Christian; Francisco Esquembre; Zhiming Darren TAN
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
[text]
Version:
Other Resources
[text]
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Z. Darren Tan
- Parent Category: 03 Motion & Forces
- Category: 02 Dynamics
- Hits: 2933