Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits


![]()
 This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Wolfgang Christian; Flix Jess Garcia Clemente
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Wolfgang Christian; Flix Jess Garcia Clemente
Kinematics Study Guide: Understanding Motion in One Dimension
Short Answer Questions
- Differentiate between distance and displacement.
- Define average speed and instantaneous speed. Provide an example of each.
- Explain the concept of acceleration. What does it mean for an object to have positive, negative, and zero acceleration?
- Describe the relationship between the gradient of a displacement-time graph and the velocity of an object.
- How can you determine the acceleration of an object from a velocity-time graph?
- What does the area under a velocity-time graph represent?
- Sketch a velocity-time graph for an object moving with uniform acceleration. Label the axes and indicate the initial and final velocities.
- Explain how the shape of a displacement-time graph can indicate whether an object is at rest, moving with uniform velocity, or moving with non-uniform velocity.
- Describe the motion of an object that has a horizontal line on its velocity-time graph.
- A car travels at a constant speed of 20 m/s for 10 seconds, then accelerates uniformly to 30 m/s over the next 5 seconds. Draw a velocity-time graph to represent this motion.
Short Answer Key
- Distance is the total length of the path traveled by an object, while displacement is the overall change in position, measured as the shortest distance between the starting and ending points. Distance is a scalar quantity, while displacement is a vector quantity.
- Average speed is the total distance traveled divided by the total time taken, while instantaneous speed is the speed at a specific moment in time. Example: A car traveling 100 km in 2 hours has an average speed of 50 km/h. The car's speedometer reading at any given moment indicates its instantaneous speed.
- Acceleration is the rate of change of velocity over time. Positive acceleration means the object's velocity is increasing, negative acceleration (deceleration) means the velocity is decreasing, and zero acceleration means the velocity is constant.
- The gradient of a displacement-time graph represents the velocity of the object. A steeper gradient indicates a higher velocity.
- The acceleration of an object is represented by the gradient of its velocity-time graph. A steeper gradient signifies a greater acceleration.
- The area under a velocity-time graph represents the displacement of the object.
- The graph should have time on the x-axis and velocity on the y-axis. The line should be straight and sloped upwards, representing increasing velocity. The initial velocity should be marked at the beginning of the line and the final velocity at the end.
- A horizontal line indicates the object is at rest. A straight line with a non-zero slope signifies uniform velocity. A curved line represents non-uniform velocity.
- An object with a horizontal line on its velocity-time graph is moving at a constant velocity.
- The graph should have time on the x-axis and velocity on the y-axis. The first part of the graph should be a horizontal line at 20 m/s for 10 seconds. The second part should be a straight line sloping upwards from 20 m/s to 30 m/s over 5 seconds.
Essay Questions
- Discuss the differences between scalar and vector quantities. Explain how these differences are significant when analyzing the motion of an object.
- A ball is thrown vertically upwards and then falls back down to its starting point. Analyze the ball's motion, describing the changes in velocity and acceleration throughout its journey.
- Explain how displacement-time and velocity-time graphs can be used to analyze the motion of an object. Include examples of different motion scenarios and how they are represented on each type of graph.
- Analyze the motion of a skydiver falling from an airplane, considering the effects of air resistance. Describe the changes in velocity and acceleration as the skydiver deploys their parachute.
- Discuss the key concepts of uniformly accelerated motion. Derive the equations of motion for an object moving with constant acceleration and explain their applications in solving problems.
Glossary of Key Terms
- Kinematics: The branch of mechanics concerned with the motion of objects without considering the forces causing the motion.
- Displacement: The overall change in position of an object, measured as the shortest distance between the starting and ending points. It is a vector quantity.
- Distance: The total length of the path traveled by an object. It is a scalar quantity.
- Speed: The rate at which an object covers distance. It is a scalar quantity.
- Velocity: The rate of change of displacement over time. It is a vector quantity that includes both speed and direction.
- Average Speed: The total distance traveled divided by the total time taken.
- Instantaneous Speed: The speed of an object at a particular moment in time.
- Acceleration: The rate of change of velocity over time. It is a vector quantity.
- Uniform Acceleration: Constant acceleration, meaning the velocity changes at a steady rate.
- Non-uniform Acceleration: Changing acceleration, meaning the velocity changes at a varying rate.
- Displacement-Time Graph: A graph that plots an object's displacement against time.
- Velocity-Time Graph: A graph that plots an object's velocity against time.
- Gradient: The slope of a line on a graph, representing the rate of change.
- Area Under a Curve: On a graph, the area enclosed between a curve and the horizontal axis. In a velocity-time graph, it represents the displacement.
- Scalar Quantity: A quantity that has only magnitude (size).
- Vector Quantity: A quantity that has both magnitude (size) and direction.
Briefing Doc: Kinematics and the "Moving Car 1D" Simulation
Sources: Excerpts from "Kinematics or Moving Car 1D JavaScript HTML5 Applet Simulation Model" on Open Educational Resources / Open Source Physics @ Singapore website.
Main Themes:
- Kinematics: The study of motion without considering the forces causing it. This resource focuses on displacement, speed, velocity, and acceleration in one dimension.
- Graphical Analysis of Motion: Using displacement-time and velocity-time graphs to understand and interpret different types of motion (at rest, uniform velocity, uniform acceleration, non-uniform acceleration).
- Educational Technology: Utilizing interactive simulations and online resources to enhance student learning in physics. The "Moving Car 1D" simulation provides a visual and interactive way for students to explore the concepts of kinematics.
Most Important Ideas/Facts:
- Learning Objectives: The resource aims to equip students with the ability to:
- Define and use key terms like displacement, speed, velocity, and acceleration.
- Represent these quantities graphically.
- Interpret the meaning of gradients and areas in motion graphs.
- Derive and apply equations of motion for uniformly accelerated linear motion.
- Describe motion under gravity with and without air resistance.
- Analyze motion with constant velocity in one direction and constant acceleration in a perpendicular direction.
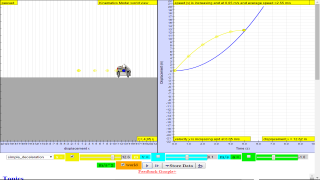
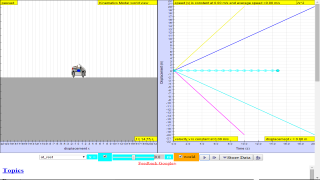
- Simulation Features: The "Moving Car 1D" simulation allows users to:
- Choose from various motion scenarios (at rest, constant velocity, constant acceleration, etc.).
- Observe the motion of the car visually.
- Analyze the corresponding displacement-time and velocity-time graphs.
- Explore mathematical models representing different motion types.
- Pedagogical Approaches: The resource emphasizes:
- Inquiry-based learning: Posing key questions to stimulate student exploration and understanding. How can we describe the motion of objects moving in a straight line?
- Progressive mathematical modeling: Encouraging students to develop and refine mathematical representations of motion. For a constant velocity motion of v=1m/s, X=1t*
- Addressing misconceptions: Recognizing and tackling common student difficulties in understanding kinematics concepts.
- Use of technology: Leveraging simulations, online learning platforms, and multimedia resources to enhance engagement and learning.
Quotes:
- "Physical quantities can be scalar (e.g., distance, speed) or vector (e.g., displacement, velocity, acceleration) quantities. Scalar quantities can be added algebraically. Vector quantities can be added using graphical methods." - This highlights the importance of distinguishing between scalar and vector quantities in kinematics.
- "Students often view the position and velocity graphs as the actual path of the object, rather than a graphical representation of an object’s motion." - This identifies a common misconception that educators should address.
Overall, this resource provides a comprehensive approach to teaching kinematics. It combines theoretical concepts with interactive simulations and practical pedagogical strategies to enhance student understanding and address common learning challenges.
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.kinematicsapp414497

https://itunes.apple.com/us/app/kinematics-simulator/id1190809767?mt=8
Learning Objectives
Candidates should be able to:
(a) define and use displacement, speed, velocity and acceleration
(b) use graphical methods to represent distance, displacement, speed, velocity and acceleration
(c) identify and use the physical quantities from the gradients of displacement-time graphs and areas under and gradients of velocity-time graphs, including cases of non-uniform acceleration
(d) derive, from the definitions of velocity and acceleration, equations which represent uniformly accelerated motion in a straight line
(e) solve problems using equations which represent uniformly accelerated motion in a straight line, including the motion of bodies falling in a uniform gravitational field without air resistance
(f) describe qualitatively the motion of bodies falling in a uniform gravitational field with air resistance
(g) describe and explain motion due to a uniform velocity in one direction and a uniform acceleration in a perpendicular direction.
Pre-requisites
You should have an understanding of the following:
-
Displacement
-
Speed and velocity
-
Acceleration
-
Gradient of a velocity-time graph
-
Area under a velocity-time graph
-
Able to plot and interpret velocity-time graph.
For Teachers' Reference:
| Theme/Topic | Kinematics/ Velocity-Time Graph |
|
Learning Outcomes
|
At the end of the lesson, students will be able to:
|
| 21CC |
At the end of the lesson, students will be able to:
|
| Success Criteria | I can:
|
Practice
https://goo.gl/forms/hreYmzgHZpmhwCxw1
Key inquiry question:
How can we describe the motion of objects moving in a straight line?
1. Speed, velocity and acceleration
• Physical quantities can be scalar (e.g. distance, speed) or vector (e.g. displacement, velocity, acceleration) quantities. Scalar quantities can be added algebraically. Vector quantities can be added using graphical methods (parallelogram method or ‘head-to-tail’ method).
• Average speed of a body is given by total distance travelled / total time taken (v = d/t). Instantaneous speed is the speed at any instant.
• Acceleration of a body is defined as its change in velocity / time taken (a = (v - u)/t). The direction of acceleration is the direction of the change in velocity.
• Acceleration is: zero when velocity is constant (i.e. no change in velocity); positive (object is accelerating) when velocity is increasing; negative (object is decelerating) when velocity is decreasing
2. Graphical analysis of motion
• Displacement-time and velocity-time graphs of a body allow us to deduce when the body is: at rest; moving with uniform velocity and acceleration; moving with non-uniform velocity and acceleration.
• Gradient of a displacement-time graph gives the velocity of the moving object; Gradient of a velocitytime graph gives the acceleration of the moving object; Area under a velocity-time graph gives the displacement travelled by a body.
Students’ prior knowledge of Kinematics
Primary level:
Students will not have been introduced to the concepts to describe motion. They would have knowledge of the effects of a force to stop or move an object; change its speed (move faster or slower) or direction of motion.
Lower secondary level:
Students learn that speed:
• is a measure of how fast an object is moving;
• depends on the distance (length) travelled and the time taken (unit: m/s).
Objects usually do not move at the same speed, hence, it is more useful to measure its average speed which is defined as total distance travelled / total time taken. Speed at any instant is the average speed over an extremely short time interval.
Students’ common misconceptions and learning difficulties in Kinematics
Displacement, velocity and acceleration:
Students’ concepts of displacement, velocity, and acceleration are not well differentiated.
They often think that: same position means same velocity for two objects; same velocity means same acceleration for two objects; larger (or smaller) velocity means larger (or smaller) acceleration; zero velocity means zero acceleration; and acceleration and velocity are always in the same direction.
Displacement-time and velocity-time graphs: Students often view the position and velocity graphs as the actual path of the object, rather than a graphical representation of an object’s motion
Worksheet
- ejss_model_kinematics Motion in One Dimension student worksheet (2017)v3dl.docx by Dave
- ejss_model_kinematics CT_kinematics (1017).ppt 2017 by Dave
- ejss_model_kinematics Motion in One Dimension student worksheet (2017).docx 2017 by Dave
- Slides for Workshop Link1 , Link2 2016
- Final version Link1, Link2 by Lyna, Gavin, Dave and lookang 2016
- Motion in One Dimension student worksheet (dl-gwf) Link1, Link2 by Lyna, Gavin, Dave and lookang 2016
Video
- https://youtu.be/ZYIeBKDBXU8 Kinematics 1d simulation video tutorial with modeling pedagogy by lookang lawrence wee
- https://youtu.be/SsSPd6I4BnA Kinematics 1D simulation running on hmtl5 Modeling pedagogy 2 by lookang lawrence wee
- Kinematics Simulation - Secondary & JC by Dave Lommen
- https://www.youtube.com/watch?v=96gBQqgWwkM by ETDtogo
- https://www.youtube.com/watch?v=-RfbnnqgOvk by ETDtogo
- https://notebooklm.google.com/notebook/725518c6-313c-4719-8e0a-8f84b111f437/audio
Pedagogical Writeup
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Mystery | |
Technology:
mystery could take the form an describe it all equation, called model.
Give the challenge to solve the mystery of a predictive equation that can be use to tell the future, more precisely the movement of a car, in a physics lesson.
Through the model selected by the students, it gives an indication of the students prior knowledge about what they know now, so that the teacher can understand the gaps of understanding for personalised mentoring https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/38-kinematics-1d
| Process | Lesson Implementation | |
| Sub-Process(es) | Introducing the Lesson / Arousing and Sustaining Interest | |
| Teaching Action | Little Professor/Little Teachers | |
Technology:
use exisiting schools' learning management system such as https://www.edmodo.com/ or Whatapp group chat to allow of arousing and sustaining interest.
Other simulations
- http://www.physicsclassroom.com/Physics-Interactives/1-D-Kinematics/Graphs-and-Ramps
- http://www.thephysicsaviary.com/Physics/Programs/Labs/EquationsOfMotionLab/index.html
- http://ophysics.com/k5.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
- http://ophysics.com/k6.html by This email address is being protected from spambots. You need JavaScript enabled to view it.
- https://www.physicsclassroom.com/Concept-Builders/Kinematics/Velocity-Time-Graphs/Concept-Builder
SLS lessons
Project related:
- AEP 03/16 LW Apps as Virtual Lab
- Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction Project Number: OER 10/15 GWF Project Duration: 01 July 2015 - 30 April 2017 http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Secondary | Primary | ||||||||||||||||||||
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion DescriptionThis simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example (ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (i) at rest , (ii) moving with uniform velocity (eg, no acceleration) (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest example of progressive mathematical model is encouraged X = 0 (ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 (g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration Version:Translations
Credits
|
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion DescriptionThis simulation has a drop-down menu for exploration of(i) at rest use of progressive mathematical model is encouraged X = 0 for example (ii) moving with uniform velocity, use of progressive mathematical model is encouraged for example X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged for example X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (i) at rest , (ii) moving with uniform velocity (eg, no acceleration) (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (i) at rest example of progressive mathematical model is encouraged X = 0 (ii) moving with uniform velocity example of progressive mathematical model is encouraged X = 1*t for a constant velocity motion of v =1 m/s (iii) moving with non-uniform velocity example of X = 0.5*1*t^2 for a constant acceleration motion of a =1 m/s^2 (g) deduce from the shape of a velocity-time graph when a body is: (i) at rest (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration Version:Translations
Credits
|
||||||||||||||||||||
Kinematics FAQs
1. What is kinematics?
Kinematics is the branch of physics that deals with the motion of objects without considering the forces causing the motion. It focuses on concepts like displacement, speed, velocity, and acceleration.
2. What are the basic concepts of kinematics?
The basic concepts of kinematics are:
- Displacement: The change in position of an object. It is a vector quantity, meaning it has both magnitude and direction.
- Speed: The rate at which an object covers distance. It is a scalar quantity, meaning it has only magnitude.
- Velocity: The rate at which an object changes its displacement. It is a vector quantity.
- Acceleration: The rate at which an object changes its velocity. It is a vector quantity.
3. What types of motion are studied in kinematics?
Kinematics studies various types of motion, including:
- Uniform motion: Motion with constant velocity.
- Non-uniform motion: Motion with changing velocity.
- Uniformly accelerated motion: Motion with constant acceleration.
- Non-uniformly accelerated motion: Motion with changing acceleration.
4. How are graphs used to represent motion?
Graphs are powerful tools for visualizing and analyzing motion.
- Displacement-time graphs: Show how an object's position changes over time. The slope of the graph represents velocity.
- Velocity-time graphs: Show how an object's velocity changes over time. The slope represents acceleration, and the area under the curve represents displacement.
5. What are some common misconceptions about kinematics?
Some common misconceptions include:
- Confusing position, velocity, and acceleration: These are distinct concepts with different meanings.
- Assuming larger velocity always means larger acceleration: Acceleration depends on the change in velocity, not just the magnitude.
- Thinking zero velocity means zero acceleration: An object can have zero velocity at a particular instant while still accelerating (e.g., at the highest point of a ball thrown upwards).
- Interpreting graphs as the actual path of the object: Graphs represent the relationship between variables, not the physical path.
6. How is kinematics applied in real life?
Kinematics has applications in numerous fields, including:
- Designing vehicles and transportation systems.
- Analyzing the motion of projectiles and satellites.
- Understanding and predicting the movement of celestial bodies.
- Developing robotics and automation systems.
7. What are some resources for learning more about kinematics?
- Textbooks: Physics textbooks at the high school or introductory college level typically have comprehensive chapters on kinematics.
- Online resources: Websites like Khan Academy and Physics Classroom provide explanations, simulations, and practice problems.
- Simulations: Interactive simulations, like the one mentioned in the provided source, offer a visual and engaging way to explore kinematics concepts.
8. How can I improve my understanding of kinematics?
- Focus on understanding the definitions and relationships between key concepts.
- Practice interpreting and drawing motion graphs.
- Work through problem sets and apply kinematics equations to solve real-world scenarios.
- Use online simulations to visualize and experiment with different types of motion.
- Details
- Parent Category: 03 Motion & Forces
- Category: 01 Kinematics
- Hits: 39256


.png
)