About
Topics
KinematicsSpeed, velocity and acceleration
Graphical analysis of motion
Free-fall
Effect of air resistance
Description
This simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged
(iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged
When only the velocity-time graph check-box is selected, it can be explored for the following cases too.
(ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t
(iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t
(iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes).
The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2.
Lastly, by selecting the 3 options of
"free fall"
"free_fall_with_small_air_resistance"
"free_fall_with_large_air_resistance"
It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration.
Sample Learning Goals
(f) deduce from the shape of a displacement-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with non-uniform velocity
(g) deduce from the shape of a velocity-time graph when a body is:
(ii) moving with uniform velocity
(iii) moving with uniform acceleration
(iv) moving with non-uniform acceleration
(i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2
(j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity
Version:
ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg
http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
|
Title |
Authors |
Level |
Type |
Updated |
Share an activity! email
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Briefing Document: Free Fall Simulation Model
1. Overview
This document reviews a JavaScript HTML5 applet simulation model focused on primary kinematics in the vertical (Y) direction, specifically addressing free fall. This model, available through the Open Educational Resources / Open Source Physics @ Singapore platform, provides an interactive way to explore the concepts of kinematics, including displacement, velocity, acceleration, and the effects of air resistance. The simulation aims to help students visualize and understand these concepts through graphical analysis and exploration of various scenarios. There are multiple versions of this model for different educational levels (primary, secondary and junior college), showing the versatility of the simulation for use in differing levels.
2. Key Themes & Concepts
- Kinematics: The simulation primarily focuses on kinematics, which is the study of motion without considering the forces that cause it. Key kinematic concepts explored include displacement, velocity, and acceleration.
- Free Fall: A central theme of the simulation is free fall, which involves the motion of an object under the influence of gravity alone (ignoring air resistance). The simulation allows students to explore free fall in ideal conditions as well as with varying degrees of air resistance.
- Graphical Analysis: A significant part of the learning experience is centered around analyzing displacement-time and velocity-time graphs. The simulation allows users to visualize these graphs and deduce properties of motion.
- Mathematical Modeling: The simulation encourages the use of progressive mathematical models to describe motion. The equations provided in the description highlight the relationship between displacement, initial velocity, time, and acceleration.
- Air Resistance: The simulation allows users to explore the impact of air resistance on free fall. Students can observe how small and large air resistance affects the motion and the attainment of terminal velocity.
- Terminal Velocity: The simulation introduces the concept of terminal velocity, which occurs when the drag force due to air resistance balances the weight of an object, resulting in zero acceleration and a constant velocity.
- Constant Acceleration: The model highlights that the acceleration of free fall near the Earth is approximately constant (9.81 m/s² or approximately 10 m/s²) when air resistance is negligible.
3. Simulation Functionality & Features
- Drop-Down Menu Exploration: The simulation uses a drop-down menu to enable users to explore different motion scenarios:
- Object at rest
- Object moving with uniform velocity
- Object moving with non-uniform velocity (constant acceleration)
- When only velocity-time is selected, users can explore non-uniform acceleration.
- Free Fall Scenarios: The simulation allows users to select between:
- "free fall" (no air resistance)
- "free_fall_with_small_air_resistance"
- "free_fall_with_large_air_resistance"
- Graphical Representation: Users can view displacement-time and velocity-time graphs, which are useful for interpreting the motion of the object.
- Embeddable Model: The simulation can be embedded into webpages via an iframe, making it easily accessible to educators and learners.
4. Sample Learning Goals
The listed sample learning goals explicitly outline what the simulation is intended to teach:
- (e) plot and interpret a displacement-time graph and a velocity-time graphThis emphasizes the importance of graphical analysis in understanding motion.
- (f) deduce from the shape of a displacement-time graph when a body is:(i) at rest
- (ii) moving with uniform velocity
- (iii) moving with non-uniform velocity
- This highlights the relationship between the shape of the displacement-time graph and the type of motion.
- (g) deduce from the shape of a velocity-time graph when a body is:(i) at rest
- (ii) moving with uniform velocity
- (iii) moving with uniform acceleration
- (iv) moving with non-uniform acceleration
- This focuses on interpreting velocity-time graphs to understand different motion behaviors.
- (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2This specifies the expected knowledge regarding the acceleration due to gravity.
- (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocityThis addresses the combined influence of gravity and air resistance and how they lead to terminal velocity.
5. Mathematical Models Presented:
- y = 0This is a model to explore the state of rest where there is zero change in vertical position.
- Y = Y0 + u*tThis equation represents motion with uniform velocity, where Y is the final position, Y0 is the initial position, u is the uniform velocity, and t is the time. This model will help students visualise motion in the y direction at a constant speed.
- Y = Y0 + ut + 0.5g*t^2This equation represents motion with uniform acceleration (like free fall with constant acceleration), where g is the acceleration due to gravity.
6. Example Questions and Answers
The source includes example questions to test student understanding:
- Sky Diver Problem: This problem explores the concept of relative motion and how constant acceleration affects the speed and position of two objects falling with a time delay. It highlights that the difference in speeds remains constant but the distance between the divers increases with time.
- “after t =2 s, the difference is always the same difference as shown by the constant difference.”
- “after t =2 s, the difference in position increases as shown by the increasing difference of YELLOW minus BLUE line.”
- Tennis Ball Throw Problem: This problem focuses on applying kinematic equations to find the time taken to reach maximum height, maximum height, time to return to the starting point, velocity at the starting point and at a specific time after the ball is thrown. It reinforces understanding of projectile motion. Some of the example answers are:
- “suggested answer: t = 2.0 s” for time at maximum height.
- “suggested answer: H maximum = 70.4 m” for maximum height.
- “suggested answer: t = 4.0 or 4.1 s” for the time at which the ball returns to the height from which it was thrown.
- “suggested answer: v = -20.2 m/s” for the velocity of the ball at the same point.
- “suggested answer: y = 27.4 m and v = -29.1 m/s” for velocity and position at t=5s.
7. Additional Resources and Context
- The resource provides links to blog posts which offer some background and updates to the simulation.
- The simulation is part of a larger project aimed at improving teacher learning and conceptual instruction using open-source physics tools.
- It mentions other hands-on kits and related resources for teaching kinematics and free fall, providing various options for teachers and students.
- It has a wide variety of resources available for use by students and teachers for a variety of physics concepts.
8. Target Audience
Based on the provided information, this resource is designed for students learning introductory physics, particularly those at the primary, secondary and junior college level. The range of resources and the inclusion of both basic and complex scenarios suggest this resource is suitable for a wide range of education levels.
9. Conclusion
The "Primary Kinematics in Y direction or Free Fall JavaScript HTML5 Applet Simulation Model" is a valuable tool for teaching and learning about kinematics, free fall, and the effects of air resistance. It combines interactive simulation with graphical analysis, helping students visualize abstract physics concepts. The inclusion of learning goals and sample questions allows for structured learning and provides guidance on what key concepts students are expected to understand from this resource. The versatility of the simulation and availability of links to additional content make this a comprehensive tool that can be used in classrooms, and also at home with independent study.
Kinematics and Free Fall Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- What are the three options for exploring motion in the provided simulation?
- What is the approximate value of acceleration due to gravity near the Earth's surface, according to the source material?
- What is the definition of terminal velocity, as explained in the source?
- According to the source material, what do displacement-time graphs reveal about a body's motion?
- According to the source material, what do velocity-time graphs reveal about a body's motion?
- According to the provided example, do two skydivers falling one after the other maintain a constant difference in speeds? Explain.
- According to the provided example, does the vertical distance between two skydivers falling one after another remain constant? Explain.
- In the tennis ball example, what is the key difference between the velocity at the start and return to the launch point?
- According to the source, what types of motion can be explored using the velocity-time graph check-box in the simulation?
- What is the general form of the equation to use when modeling uniform acceleration, according to the text?
Answer Key
- The simulation explores motion for objects that are (i) at rest, (ii) moving with uniform velocity, and (iii) moving with non-uniform velocity (such as constant acceleration).
- The acceleration of free fall for a body near the Earth is stated to be constant and approximately 10 m/s².
- Terminal velocity is a constant velocity reached when the weight of a falling object is balanced by the drag force of air resistance, resulting in zero acceleration.
- Displacement-time graphs can reveal if a body is at rest, moving with uniform velocity (straight line slope), or moving with non-uniform velocity (curved line).
- Velocity-time graphs can show if a body is at rest (zero velocity line), moving with uniform velocity (horizontal line), moving with uniform acceleration (straight slope), or moving with non-uniform acceleration (curved slope).
- The difference in their speeds does stay the same throughout the fall as the air resistance is ignored and both are accelerating at the same rate.
- The vertical distance between the two skydivers does not stay the same; it increases over time due to their constant acceleration and starting separation, thus the constant rate of change in their speeds.
- The velocity of the ball at the return point is the negative of the initial velocity at the start, meaning it has the same speed but in the opposite direction.
- The velocity-time graph check-box allows exploring cases including at rest, uniform velocity, uniform acceleration, and non-uniform acceleration.
- The general form for modeling uniform acceleration is given as Y = Y0 + ut + 0.5g*t², where Y0 is initial position, u is initial velocity, t is time, and g is acceleration.
Essay Questions
Instructions: Answer each of the following questions in a detailed essay format.
- Discuss how the provided simulation can be used to understand the relationship between displacement-time graphs and velocity-time graphs, particularly in the context of free fall with varying air resistance.
- Analyze the learning goals related to interpreting graphs (displacement-time and velocity-time) and explain how they relate to conceptual understanding of motion.
- Compare and contrast the motion of an object in free fall with and without air resistance, using the provided simulation as a point of reference, and discuss the role of terminal velocity.
- Evaluate the provided skydiver and tennis ball examples and use them to demonstrate the principles of kinematics, including the importance of initial velocity and acceleration.
- Explain the significance of the JavaScript HTML5 Applet Simulation Model as an educational tool for visualizing and understanding complex concepts related to kinematics and free fall.
Glossary of Key Terms
- Kinematics: The branch of mechanics concerned with the motion of objects without reference to the forces which cause the motion.
- Free Fall: The motion of an object where the only force acting upon it is gravity, neglecting air resistance.
- Uniform Velocity: Motion with constant speed in a constant direction, meaning zero acceleration.
- Non-Uniform Velocity: Motion where the speed or direction is changing; indicating acceleration.
- Uniform Acceleration: Motion with a constant rate of change of velocity.
- Non-Uniform Acceleration: Motion where the rate of change of velocity is not constant.
- Displacement-Time Graph: A graph that plots the position of an object against time, and where the slope of the line shows velocity.
- Velocity-Time Graph: A graph that plots the velocity of an object against time, and where the slope of the line shows acceleration.
- Terminal Velocity: The constant velocity of a falling object when the force of air resistance equals the force of gravity, leading to zero net acceleration.
- Air Resistance (Drag Force): The force exerted by air on an object moving through it, that acts in the opposite direction to motion, thus slowing the object.
Worksheet
Examples
From Dave and Gavin,
1.A sky diver jumps out of a hovering helicopter. A 2 seconds afterwards another sky diver jumps out and they both fall along the same vertical line. Ignore air resistance so that both sky divers fall with the same acceleration.
a.Does the difference in their speeds stay the same throughout the fall?
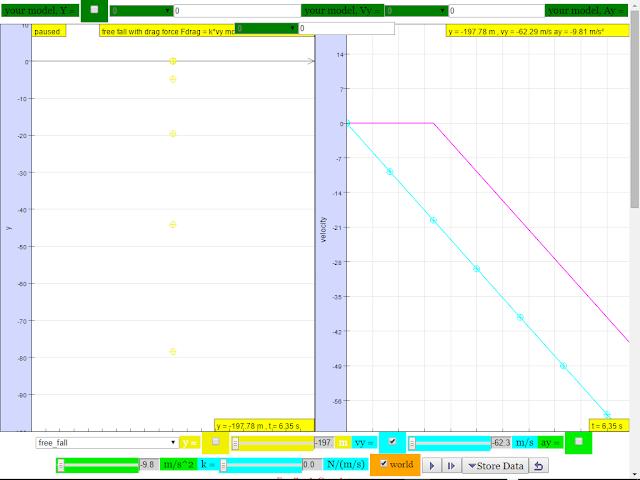 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference is always the same difference as shown by the constant difference.
b.Does the vertical distance between them stay the same throughout the fall?
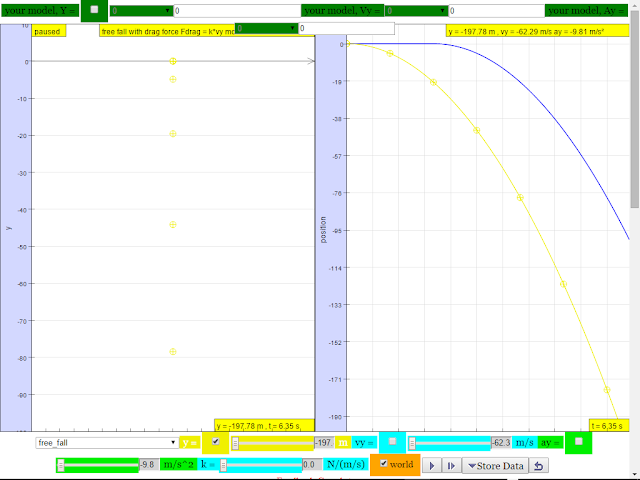 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: after t =2 s, the difference in position increases as shown by the increasing difference of YELLOW minus BLUE line.
Question 2
2.A tennis ball thrown from the top of a building is given an initial velocity of 20 m/s straight upward. The building is 50 m high, and the ball just misses the edge of the roof on its way down. Using t = 0 as the time the ball leaves the thrower’s hand, determine
a.the time at which the ball reaches its maximum height
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 2.0 s
b.the maximum height
suggested answer: H maximum = 70.4 m
c.the time at which the ball returns to the height from which it was thrown
 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
suggested answer: t = 4.0 or 4.1 s
d.the velocity of the ball at this instant
suggested answer: v = -20.2 m/s
e.the velocity and position of the ball at t = 5 s
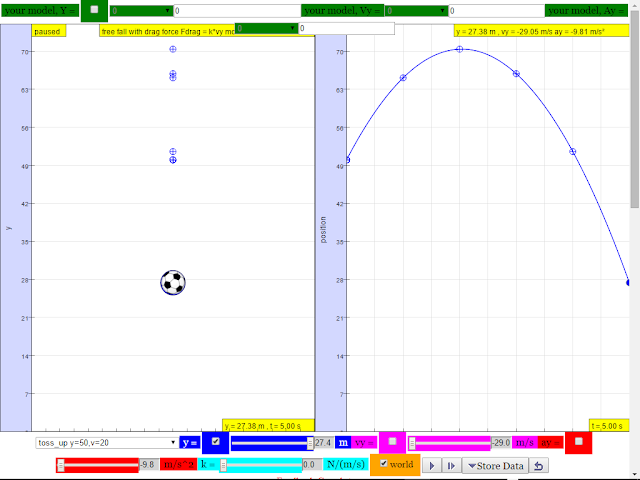 |
| https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/01-kinematics/37-kinematics-in-y-direction |
Versions
- http://weelookang.blogspot.sg/2016/01/ejss-free-fall-simulation-added-more.html Blogpost on more cases added
- http://weelookang.blogspot.sg/2014/03/ejss-kinematics-in-y-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.html Blogpost on JavaScript version by Loo Kang Wee
- http://weelookang.blogspot.sg/2013/12/ejss-kinematics-model.html template objects from lookang
- http://weelookang.blogspot.sg/2010/09/ejs-open-source-bouncing-ball-with-drag.html Blogpost on Java vesion by Loo Kang Wee and Fu-Kwun Hwang
- http://weelookang.blogspot.sg/2010/06/ejs-open-source-kinematics-java-applet.html
- http://www.compadre.org/osp/items/detail.cfm?ID=13050 Physlet One-Dimensional Kinematics Illustrations Package by Andreu Glasmann, Wolfgang Christian, and Mario Belloni
Other Resources
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=421.0 Elastic bouncing ball Java Version by Fu-Kwun Hwang
- http://butikov.faculty.ifmo.ru/Projects/Falling_bodies.html#_applet Falling Object Java 3D version by Eugene Butikov
Other Hands-on kit
- https://sites.google.com/site/iprofmeca/session-1-free-fall by This email address is being protected from spambots. You need JavaScript enabled to view it.
- http://www.addest.com/products/category/Science_Kits by Addest Technovation
 Kinematics Kit
Kinematics Kit - http://www.addest.com/products/category/Science_Kits by Addest Technovation
 Free Fall Kit
Free Fall Kit
Project related:
Understanding Teacher Learning Community as Support for Implementation of Open Source Physics for Conceptual Instruction
Project Number: OER 10/15 GWF
Project Duration: 01 July 2015 - 30 April 2017
http://weelookang.blogspot.sg/2015/07/understanding-teacher-learning.html
Family of Resources
| Secondary | Junior College | ||||||||||||||||||||||||||||||||||||||||
About
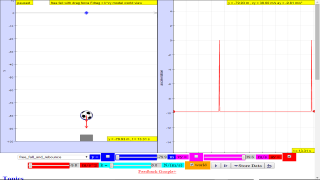
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:ball taken from: http://psychology.wikia.com/wiki/File:Soccer_ball.svg http://weelookang.blogspot.sg/2013/12/ejss-free-fall-model.htmlFor Teachers
Teacher-Submitted Activities
Share an activity! email Translations
Credits
|
About
TopicsKinematicsSpeed, velocity and acceleration Graphical analysis of motion Free-fall Effect of air resistance DescriptionThis simulation has a drop-down menu for exploration of(ii) moving with uniform velocity, use of progressive mathematical model is encouraged (iii) moving with non-uniform velocity (eg, constant acceleration) use of progressive mathematical model is encouraged When only the velocity-time graph check-box is selected, it can be explored for the following cases too. (ii) moving with uniform velocity (eg, no acceleration) model of the form Y = Y0+u*t (iii) moving with uniform acceleration (eg, constant acceleration = 9.81 m/s^2) model of the form Y = Y0+u*t+0.5*g*t (iv) moving with non-uniform acceleration (eg, with small ot large drag force acting thus acceleration changes). The default acceleration is set at-9.81 m/s^2 which is near to the Earth is constant and is approximately 10 m/s 2. Lastly, by selecting the 3 options of "free fall" "free_fall_with_small_air_resistance" "free_fall_with_large_air_resistance" It can provide the experience and evidences for describing the motion of bodies with constant weight falling with (large and small) or without air resistance, including reference to terminal velocity, a constant velocity as a result of balanced forces of weight of mass and the drag force giving rise to zero acceleration. Sample Learning Goals
(e) plot and interpret a displacement-time graph and a velocity-time
graph
(f) deduce from the shape of a displacement-time graph when a body is: (ii) moving with uniform velocity (iii) moving with non-uniform velocity (g) deduce from the shape of a velocity-time graph when a body is: (ii) moving with uniform velocity (iii) moving with uniform acceleration (iv) moving with non-uniform acceleration (i) state that the acceleration of free fall for a body near to the Earth is constant and is approximately 10 m/s 2 (j) describe the motion of bodies with constant weight falling with or without air resistance, including reference to terminal velocity Version:Translations
Credits
|
||||||||||||||||||||||||||||||||||||||||
FAQ on Free Fall and Kinematics Simulations
- What is the main focus of the "Primary Kinematics in Y direction or Free Fall JavaScript HTML5 Applet Simulation Model"?
- This simulation is primarily designed to explore the concepts of kinematics, particularly focusing on motion in the vertical (Y) direction, which is commonly referred to as free fall. It enables users to investigate the effects of various factors like initial velocity, uniform acceleration (specifically gravity), and air resistance on the motion of objects. The simulation uses mathematical models and graphical analysis to demonstrate these principles.
- What types of motion can be simulated using the applet?
- The applet allows for simulating several types of motion, including: (i) objects at rest, (ii) objects moving with uniform velocity (constant speed and direction), (iii) objects moving with uniform acceleration (like free fall under gravity), and (iv) objects moving with non-uniform acceleration (where acceleration changes over time due to drag force or other factors). These simulations can be analyzed using displacement-time and velocity-time graphs.
- How does the simulation demonstrate the effect of air resistance on falling objects?
- The simulation includes options for exploring free fall with and without air resistance, specifically including "free fall," "free_fall_with_small_air_resistance," and "free_fall_with_large_air_resistance" options. This helps users observe how air resistance affects the acceleration of a falling object, eventually leading to a constant terminal velocity when the drag force balances the weight of the object resulting in zero acceleration.
- What are some learning goals associated with using this simulation?
- Some of the key learning goals include: the ability to plot and interpret displacement-time and velocity-time graphs; the ability to deduce the motion of a body (whether at rest, moving with uniform velocity, or moving with non-uniform velocity) from displacement-time graphs; the ability to deduce the motion of a body (whether at rest, moving with uniform velocity, moving with uniform acceleration, or moving with non-uniform acceleration) from velocity-time graphs; understanding that the acceleration due to free fall near Earth is approximately 10 m/s², and the ability to describe the motion of falling bodies with and without air resistance, including the concept of terminal velocity.
- Besides the simulation itself, what other resources are provided for teaching and learning about kinematics and free fall?
- The resource provides links to various other resources, such as blog posts discussing the simulation development, downloadable student worksheets, examples of solved kinematics problems, links to related simulations and tools, and resources for hands-on kits, including a range of other interactive simulations on related topics like gravity, projectile motion, and more. These materials cater to various learning and teaching styles.
- What practical examples are included to help in understanding free-fall concepts?
- The resources provide real-world examples such as a sky diver jumping out of a helicopter to explore scenarios where two objects fall with the same acceleration, but at different times. There are also problems involving a tennis ball thrown upwards from a building, requiring calculation of maximum height, time of flight and final velocity. These demonstrate free fall in the context of projectile motion.
- Can this simulation be used in various educational settings?
- Yes, the simulation is designed for both primary and secondary levels as it is available in both "Primary" and "Secondary" forms, suggesting it's suitable for a range of educational stages. The availability of different resources and versions, such as interactive simulations, and problem sets, indicates that it is meant to be versatile for different levels of physics education. It is embedded in a web page and intended for use in interactive teaching and learning.
- What kind of modeling is emphasized in the simulations?
- The simulation emphasizes the use of progressive mathematical models to represent various types of motion. The simulations explore different models such as Y=0, Y=Y0+ut, Y=Y0+ut+0.5gt^2, highlighting the connections between the mathematical descriptions and the observed motion. Users are encouraged to explore these mathematical representations along with graphical analyses to gain a deeper understanding of kinematic principles, for constant and non-constant acceleration.
- Details
- Parent Category: 03 Motion & Forces
- Category: 01 Kinematics
- Hits: 6322








.png
)


