About

<h2>Newton's cradle</h2>

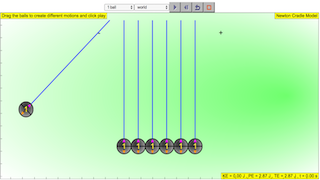
<p>Newton's cradle is a device that demonstrates conservation of momentum and energy using a series of swinging spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, transmitting a force through the stationary spheres that pushes the last sphere upward. The last sphere swings back and strikes the still nearly stationary spheres, repeating the effect in the opposite direction. The device is named after 17th-century English scientist Sir Isaac Newton. It is also known as Newton's pendulum, Newton's balls, Newton's rocker or executive ball clicker (since the device makes a click each time the balls collide, which they do repeatedly in a steady rhythm).</p>

<p>A typical Newton's cradle consists of a series of identically sized metal balls suspended in a metal frame so that they are just touching each other at rest. Each ball is attached to the frame by two wires of equal length angled away from each other. This restricts the pendulums' movements to the same plane.</p>

<h2>Controls</h2>

<p>The first comboBox allows eay selection of number of balls in the Newton's cradle</p>

<p> 1 ball to the left</p>

<p> 2 balls to the left</p>

<p> 3 balls to the left</p>

<p> 4 balls to the left</p>

<p> 5 balls to the left</p>

<p> 6 balls to the left</p>

<p> 7 balls to the left</p>

<p> 1 ball 1 raises 1 ball to the left and 1 ball to the right</p>

<p> 2 ball 1 raises 2 ball to the left and 1 ball to the right</p>

<p> 2 ball 2 raises 2 balls to the left and 2 balls to the right</p>

<p> 3 ball 3 raises 3 balls to the left and 3 balls to the right</p>

<p>n is the number of balls allowed</p>

<p>i is the index of the ball to change</p>

<p>for which m[i] is the mass of the index ball</p>

<p>play button starts the simulation</p>

<p>reset button starts the simulation at afresh</p>

<h2>Physics explanation</h2>

<p>Newton's cradle can be modeled fairly accurately with simple mathematical equations with the assumption that the balls always collide in pairs.</p>

<p> The motion of the balls are modelled using \( \frac{d\theta[i]}{dt} = \omega[i]\) </p>

<p>where \(\theta\) is the angle of the ball</p>

<p> \( \omega \) is the angular velocity </p>

<p> i represents each element of the ball</p>

<p> t is time </p>

<p> the second order differential equation is \(\frac{d(\omega[i])}{dt}=-\frac{g*sin(\theta[i])}{L}-k*L*\omega[i] \) </p>

<p> where g is gravitational constant 9.81 \(m/s^2\) </p>

<p> L is the length of the inextensible string connecting the ball to the support for rotational motion </p>

<p> k is a resistant coefficient to rotational motion \( \omega \) </p>

<h2>Events of the ordinary differential equations</h2>

<p>In a state event, a TOLERANCE =1.0e-6 is defined, a loop to check through each ball i, where a check of the \(\theta[i]\) is greater than \(\theta[i+1]\) plus the TOLERANCE, if true, return the balls to their closed up angular position \(\theta[i+1]-\theta[i]\). If false, do nothing. </p>

<p>The following actions are carried out at the end of the event</p>

<p>\(m_{1}=m[cid]\) where \(m_{1}\) is a dummy variable to contain mass of collision with index = cid</p>

<p>\(m_{2}=m[cid+1]\);where \(m_{2}\) is a dummy variable to contain mass of collision with index = cid+1</p>

<p>\(v_{1}=L*\omega[cid]\);</p>

<p>\(v_{2}=L*\omega[cid+1]\);</p>

<p>\(v_{a}=\frac{((m_{1}-m_{2})*v_{1}+2*m_{2}*v_{2})}{(m_{1}+m_{2})}\);// velocity after collision</p>

<p>\(v_{b}=\frac{(2*m_{1}*v_{1}+(m_{2}-m_{1})*v_{2})}{(m_{1}+m_{2})}\);</p>

<p>\(\omega[cid]=\frac{v_{a}}{L}\);// back to omega</p>

<p>\(\omega[cid+1]=\frac{v_{b}}{L}\);</p>

<h2>Fixed Relationship Calculations</h2>

<p>There is a for loop over i=0 to i less than number of balls to calculate the following to constraint the masses to move in pendulum-part of a circular path</p>

<p> \( dx[i]=L*(sin \theta[i]) \) where dx[i] is the change is x[i] position</p>

<p> \( dy[i]=-L*cos(\theta[i]) \) where dy[i] is the change in y[i] position</p>

<p> x[i]=xc[i]+dx[i] where xc[i] is each balls centre or equilibrium x position</p>

<p> y[i]=ymax+dy[i] where ymax is the support y position</p>

<p> \( vx[i]=L*\omega[i]*cos(\theta[i]) \) where vx[i] is the x direction linear velocities of each ball</p>

<p> \( vy[i]=L*\omega[i]*sin(\theta[i]) \) where vy[i] is the y direction linear velocities of each ball</p>

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang and lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; Francisco Esquembre

Check out Glowing Newton's Cradle Desk Ornament Small And Large Sizes With Led Lights. Get it on Shopee now! https://shope.ee/3AhkYwOP03?share_channel_code=1

20231223 Update on WEBEJS:  https://macmath.inf.um.es/editor?id=lookang&url=https%3A//iwant2study.org/lookangejss/02_newtonianmechanics_3dynamics/ejss_model_newtonscadlerealwee.zip

Briefing Document: 📔 Newton's Cradle Simulation Model

1. Introduction

This document summarizes the key information about a Newton's Cradle JavaScript HTML5 applet simulation model, hosted by "Open Educational Resources / Open Source Physics @ Singapore". This interactive model is designed as an educational tool for teaching physics concepts, specifically conservation of momentum and energy. The resource is versatile, being accessible on various devices and embeddable on web pages.

2. Main Themes

• Interactive Physics Education: The primary theme is the use of an interactive simulation to demonstrate core physics principles, specifically related to Newtonian mechanics, dynamics, and energy. This allows for a hands-on approach to learning.
• Accessibility and Versatility: The model is designed to be widely accessible, functioning across various platforms including desktops, laptops, tablets, and smartphones, and it works in web browsers via HTML5.
• Computational Modeling: The resource utilizes mathematical equations and numerical methods to simulate the behavior of the Newton's cradle, providing a glimpse into how physics phenomena are translated into computer models.

3. Important Ideas and Facts

• Newton's Cradle Functionality: The document explains the basic operation of Newton's cradle, highlighting the transfer of force and energy through a series of colliding spheres. It emphasizes that the device demonstrates the conservation of momentum and energy.
• "Newton's cradle is a device that demonstrates conservation of momentum and energy using a series of swinging spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, transmitting a force through the stationary spheres that pushes the last sphere upward."
• Physical Setup: A typical Newton's cradle is described as having identically sized metal balls suspended by two wires each, which restricts the motion to a single plane.
• Simulation Controls: The applet includes user-friendly controls, such as:
• ComboBox: A dropdown menu allows the user to easily select the number of balls initiating the swing (e.g., "1 ball to the left", "2 balls to the left," etc.,). Some settings raise balls from both sides, like "1 ball 1 raises 1 ball to the left and 1 ball to the right".
• Play Button: Initiates the simulation.
• Reset Button: Restarts the simulation.
• Mathematical Model: The physics behind the simulation is described using mathematical equations, specifically:
• Angular Velocity: The change in angle is expressed as dθ[i]/dt = ω[i], where θ is the angle and ω is the angular velocity of each ball.
• Second Order Differential Equation: The model uses the second order differential equation d(ω[i])/dt = -(g*sin(θ[i]))/L - k*L*ω[i] to calculate angular velocity, where g is the gravitational constant (9.81 m/s²), L is the string length, and k is a resistant coefficient.
• These equations represent the motion of the balls as a series of interconnected pendulums.
• Collision Events: The simulation defines a "state event" to handle collisions.
• A tolerance value of 1.0e-6 is defined to check if the angle of one ball (θ[i]) is greater than the next ball (θ[i+1]) by more than the tolerance.
• If a collision is detected, the velocities of colliding balls are updated based on the conservation of momentum. The simulation assumes only pair-wise collisions happen at one time. The variables m1, m2, v1, v2, va, and vb are used in the velocity calculation formulas. The resulting velocity calculations are then translated back into angular velocity.
• The velocity after collision (v_a and v_b) is calculated using formulas that appear to be derived from the conservation of momentum, taking into account the mass and initial velocities of each colliding ball.
• Fixed Relationship Calculations: The model includes calculations to constrain the balls' motion to a circular path.
• The position of each ball (x[i], y[i]) is calculated using trigonometric functions related to the angle (θ[i]) and length (L), such as dx[i] = L*sin(θ[i]) and dy[i] = -L*cos(θ[i]).
• Similarly, velocities (vx[i], vy[i]) are calculated by multiplying the angular velocity (ω[i]) by the radius (string length L) and using trigonometric functions vx[i] = L*ω[i]*cos(θ[i]) and vy[i]=L*ω[i]*sin(θ[i]) .
• Credits & Contributors: The simulation was created by Fu-Kwun Hwang, lookang, and Francisco Esquembre, and includes links to other resources and videos related to Newton's Cradle. The resource acknowledges several other resources and contributors, demonstrating its position within the wider open source physics education movement.
• Licensing: The resource is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License, promoting open use and sharing for educational purposes. Commercial use requires explicit contact with the developers and the associated license.

4. Intended Audience

The resource appears to be primarily aimed at:

• Secondary and Junior College students studying physics.
• Teachers looking for interactive tools to teach concepts related to dynamics, energy, and oscillations.
• Anyone interested in exploring the physics of Newton's cradle via a digital simulation.

5. Key Takeaways

• The Newton's Cradle simulation is an educational tool designed to explain the principles of energy and momentum conservation in a visual and interactive manner.
• It provides a concrete example of how mathematical models and physics concepts are used in simulations.
• The wide accessibility and user-friendly controls make it a useful resource for both in-classroom teaching and self-guided learning.
• The documentation reveals the underlying mathematics and computational approach to building simulations of physical phenomena.
• The resource is part of a larger repository of physics simulations, demonstrating an active effort to promote open source education in physics.

This briefing document provides a comprehensive overview of the provided source material, covering the key features, concepts, and intended use of the Newton's cradle simulation model.

Newton's Cradle Simulation Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What two physical principles does Newton's cradle primarily demonstrate?
2. What is the typical setup of a Newton's cradle, in terms of the spheres and their arrangement?
3. How is the motion of the pendulums restricted?
4. What do the controls of the simulation allow users to adjust, and what are some examples?
5. What is the mathematical relationship used to model the motion of each ball using angular velocity?
6. Explain the purpose of the TOLERANCE value in the state event of the simulation.
7. Describe what calculations are performed at the end of the event concerning masses and velocities.
8. Explain how the simulation constrains the movement of the balls to a pendulum-like path.
9. What does the variable dx[i] represent in the simulation's calculations?
10. Besides the simulation of the Newton's cradle, what is one other educational resource that is included in the provided text?

Quiz Answer Key

1. Newton's cradle primarily demonstrates the conservation of momentum and the conservation of energy. When one sphere is released, the momentum and energy are transferred through the other stationary spheres to move the last one.
2. A Newton's cradle typically consists of a series of identically sized metal balls, suspended in a frame so that they are just touching each other when at rest. Each ball is attached to the frame by two wires.
3. The wires are of equal length and angled away from each other, restricting the pendulums' movements to the same plane and ensuring they swing in a straight line.
4. The simulation controls include a combo box that allows the user to select the number of balls and initial positions. Examples include selecting 1 ball to the left, 2 balls to the left, or 1 ball raised to the left and 1 to the right.
5. The angular velocity ((\omega)) is the rate of change of the angle ((\theta)) of the ball with time (t), expressed as (\frac{d\theta[i]}{dt} = \omega[i]) , where i represents a specific ball.
6. The TOLERANCE value, set at 1.0e-6, helps determine if a ball's angle is significantly greater than the ball next to it. This triggers a state event where balls are returned to their closed-up angular position.
7. At the end of the event, the simulation calculates the masses and velocities of the colliding balls using dummy variables. These values are then used to determine the post-collision velocities of the two involved balls.
8. The simulation ensures the balls move along a pendulum-like path by calculating the change in x and y positions, based on the sine and cosine of the ball’s angle, relative to a fixed center and a maximum y value.
9. In the simulation's calculations, dx[i] represents the change in the x-position of each ball (i), calculated as L*(sin((\theta[i]))) where L is the length of the string.
10. One other educational resource mentioned is the "LOL Energy Stores and Transfers Diagram Master Template with ability to generate any other systems with energy stores and transfers- JavaScript Simulation Applet HTML5"

Essay Questions

Instructions: Answer the following questions in essay format.

1. Discuss how the Newton's cradle simulation demonstrates the principles of conservation of momentum and conservation of energy. Explain how the simulation models these concepts with calculations and state events.
2. Analyze the role of the mathematical equations used in the simulation to model the movement of the balls, making sure to cover the variables used and the forces in play.
3. Describe the purpose and implementation of the state event within the simulation. Detail how this component affects the simulation's behavior during collisions.
4. Compare and contrast the different settings and controls within the simulation. How can these be used to explore different aspects of the physics of a Newton's cradle?
5. Evaluate how the provided resources from Open Educational Resources / Open Source Physics @ Singapore promote interactive learning and inquiry-based education, giving reference to other resources included in the provided text.

Glossary of Key Terms

Conservation of Momentum: The principle stating that the total momentum of a system remains constant if no external forces act on it. In the case of the Newton’s cradle, the momentum is transferred through the balls during collisions. Conservation of Energy: The principle stating that the total energy of an isolated system remains constant; energy can transform from one form to another (e.g., potential to kinetic) but cannot be created or destroyed. Angular Velocity ((\omega)): The rate at which an object rotates or revolves around an axis, expressed in radians per second. Pendulum: A weight suspended from a pivot point, allowing it to swing freely under the influence of gravity, forming the basis of the motion of each ball in the Newton’s cradle. State Event: In the context of the simulation, this refers to a specific condition or trigger (e.g., when a ball's angle exceeds a certain value relative to its neighbor) that causes a particular set of calculations and actions to occur. TOLERANCE: A small numerical value (e.g. 1.0e-6) that is used to account for numerical inaccuracies in computation to detect when balls have moved beyond a threshold. Inextensible String: A string that does not stretch or change in length, used in the simulation to constrain the motion of the balls to a rotational arc. Resistant Coefficient (k): A value that represents the resistance to the rotational motion ((\omega)), incorporating factors like friction and air resistance which tend to slow down the movement of the cradle's balls. Ordinary Differential Equation: A mathematical equation that relates a function to its derivatives. Used here to model the motion of the balls by tracking the rate of change of their angular velocity. JavaScript HTML5 Applet: A type of interactive application developed using JavaScript and HTML5, designed to run within a web browser without the need for plugins, in this case creating the simulation of the Newton’s cradle.

Version:

1. http://weelookang.blogspot.sg/2015/06/ejss-newtons-cradle-model.html  by lookang

Video

https://xmphysics.wordpress.com/category/03-dynamics/  by xmphysics

https://notebooklm.google.com/notebook/3e33c5ea-ffb0-4650-8ec5-757438d823d2/audio

Other Resources

1. http://www.walter-fendt.de/html5/phen/newtoncradle_en.htm

2. See the Pen Newton's Cradle by liabru (@liabru) on CodePen.

FAQ on the Newton's Cradle Simulation

1. What is a Newton's cradle and what does it demonstrate? A Newton's cradle is a device consisting of a series of suspended spheres. It demonstrates the principles of conservation of momentum and energy. When one or more spheres are lifted and released, the momentum and energy are transferred through the stationary spheres, causing the spheres on the opposite end to swing outward. This process continues in a repeating pattern until the energy is dissipated.
2. How is the motion of the balls in the simulation mathematically modeled? The motion of the balls is modeled using differential equations. The angular velocity ((\omega)) is the rate of change of the angle ((\theta)) of each ball with respect to time ((t)), expressed as ( \frac{d\theta[i]}{dt} = \omega[i]). A second order differential equation, (\frac{d(\omega[i])}{dt}=-\frac{gsin(\theta[i])}{L}-kL*\omega[i] ), describes the angular acceleration of each ball, taking into account gravity ((g)), string length ((L)), and a resistant coefficient ((k)) to rotational motion.
3. What happens during a collision event within the simulation? In the simulation, collision events are triggered when the angle of one ball exceeds the angle of the next ball, with a defined tolerance. When a collision occurs, the simulation calculates the new velocities of the colliding balls using formulas derived from conservation of momentum, then updates the angular velocities of the balls. The simulation assumes that collisions occur between pairs of adjacent balls.
4. How are the positions and linear velocities of the balls calculated? The simulation calculates the position of each ball as a part of a circular path, as in a pendulum, using the equations: ( dx[i]=L*(sin \theta[i]) ) and ( dy[i]=-Lcos(\theta[i]) ) where dx and dy represent the changes in the x and y positions. Linear velocities are calculated using ( vx[i]=L\omega[i]cos(\theta[i]) ) and ( vy[i]=L\omega[i]*sin(\theta[i]) ) , where vx and vy are x and y direction velocities.
5. What controls are available in the simulation, and what do they do? The simulation includes controls to adjust the number of balls in the cradle and to initiate different scenarios. Users can choose the number of balls to raise on one side, or on both sides. Additionally, there are "play" and "reset" buttons to control the simulation flow.
6. What assumptions are made in the mathematical model of the Newton's Cradle simulation? The mathematical model in this simulation assumes that the balls always collide in pairs and that the connecting string is inextensible. These simplifications allow for a good and robust model.
7. Can this Newton's Cradle simulation be accessed and used on different devices? Yes, this JavaScript HTML5 simulation is designed to work across multiple platforms, including desktops, laptops, Chromebooks, and mobile devices such as phones, tablets, and iPads. The resource is available for embedding into webpages.
8. Besides the Newton's Cradle simulation, what other kinds of educational simulations does this source offer? The source offers a diverse range of interactive simulations and applets covering various topics in physics, mathematics, chemistry, and other sciences. Examples include simulations on projectile motion, optics, electromagnetism, circuits, and even simulations designed for mathematics education. There are also applets for teaching primary and secondary level literacy. The tools offer support to teachers who wish to create their own.