Translations

Code	Language		Translator	Run
id	id	id

Credits

Fu-Kwun Hwang; Loo Kang Wee

http://iwant2study.org/lookangejss/02_newtonianmechanics_5turningeffectsofforces/ejss_model_blocktiltedwee/blocktiltedwee_Simulation.xhtml

Briefing Document: Rotating Rectangular Block JavaScript HTML5 Applet Simulation Model

1. Overview

This document analyzes a resource from the Open Educational Resources / Open Source Physics @ Singapore website. The core offering is a JavaScript HTML5 applet simulation model of a rotating rectangular block. This simulation is designed to help users understand the principles of torque, rotational equilibrium, center of gravity, and stability. It is intended for secondary and junior college level students, and accessible on various platforms including desktops, laptops, tablets and smartphones.

2. Main Themes & Concepts

• Turning Effects of Forces (Torque): The simulation and accompanying text heavily emphasize the concept of torque, also referred to as the moment of a force. The key point is that: "The moment of a force (or torque) = force x perpendicular distance from the pivot." The simulation allows users to manipulate the block and observe how changes in the distance of the center of gravity from the pivot point affect stability.
• Rotational Equilibrium: The resource explains that "in a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero." A central principle, the "Principle of moments" is included, which states that for rotational equilibrium: "the sum of its clockwise moments about any point is equal to the sum of anticlockwise moments about the same point." The simulation visually demonstrates how the block will rotate or remain stable based on the balance of torques.
• Center of Gravity & Stability: The resource highlights that "The weight of a body may be taken as acting at a single point known as its centre of gravity; the position of which affects the stability of the body." Stability is defined as "a measure of a body’s ability to maintain its original position." The simulation directly allows users to manipulate the center of gravity of the block through dragging and resizing the block and to learn that "Objects may be made more stable by lowering its centre of gravity or increasing its base area."

3. Key Ideas and Facts

• Interactive Simulation: The primary learning tool is the interactive simulation applet. Users can "Drag the center of the block to make the block tilt with an angle," directly exploring the relationship between the block's position and its stability. The simulation also allows users to change the block's dimensions, adding more opportunities for exploration.
• Stability Criterion: A crucial concept demonstrated is that the block will not fall as long as "the center of gravity stay[s] inside the surface area of the object on the ground," because the torque will turn it back to its original position. However, if the center of gravity is moved outside of that support area, "the block will fall out."
• Applicability: The simulation is accessible on various platforms, making it easily usable in different educational contexts including the use of mobile phones and tablets.
• Learning Goals: The resource explicitly ties the simulation to specific inquiry questions, namely "What are the characteristics and effects of forces in nature?" Specifically referencing "Turning effects of forces and Equilibrium of forces" and "Centre of gravity and Stability"
• Open Educational Resource: This resource is part of a larger collection of Open Educational Resources, suggesting it is intended for free use and sharing in educational settings. The license provided states "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License".
• Multiple Formats: The resource is presented in various formats, including a web-embeddable iframe, an Android App, and links to other related resources and videos. The inclusion of several videos, such as "How to Teach using Simulation" indicates that it’s also a resource aimed to assist teachers in how to use simulations in their classes.
• Attribution: The creators of the applet are explicitly credited ("Fu-Kwun Hwang; Loo Kang Wee"). This suggests a collaborative effort involving multiple people.
• Remixing and Original Source: The provided material includes a link to a remix of the model and the original Java simulation, showing how users may explore and remix the content of this simulation.

4. Quotes

• "Property of a body for which a small angular displacement set up a restoring torque that tends to return the body to its original position." - Definition of rotational stability.
• "In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero." - Definition of rotational mechanical equilibrium.
• "The moment of a force (or torque) = force x perpendicular distance from the pivot." - Definition of torque.
• "Principle of moments states that for a body to be in rotational equilibrium, the sum of its clockwise moments about any point is equal to the sum of anticlockwise moments about the same point." - Definition of the principle of moments.
• "The weight of a body may be taken as acting at a single point known as its centre of gravity; the position of which affects the stability of the body." - Importance of the center of gravity.
• "Stability is a measure of a body’s ability to maintain its original position." - Definition of stability.
• "Objects may be made more stable by lowering its centre of gravity or increasing its base area." - Practical ways to increase stability.
• "Drag the center of the block to make the block tilt with an angle. As long as the center of gravity stay inside the surface area of the object on the ground, the block will not fall out." - Instruction on how to use the applet.
• "However, if the center of gravity was outside the surface area, the block will fall out!"- Explanation of what happens with an unstable condition.

5. Conclusion

This resource provides a useful, interactive simulation that helps students visualize and understand core physics concepts related to torque, rotational equilibrium, center of gravity, and stability. Its accessibility across multiple platforms and incorporation into a collection of educational materials makes it a strong example of a modern, open educational resource. The provision of video material, attribution information, and links to the original content also underscores the open nature of the project.

 

Rotating Rectangular Block Simulation Study Guide

Quiz

1. What is the key property of a body that causes it to return to its original position after a small angular displacement?
2. In a rotational mechanical equilibrium, what two conditions must be met?
3. How does the position of the center of gravity relative to the base of an object affect its stability?
4. What happens to the block in the simulation if its center of gravity is dragged outside of the base area?
5. What is the formula for the moment of a force (or torque)?
6. Give one example of a simple machine where the moment of a force is used.
7. What does the Principle of Moments state about the moments acting on a body in rotational equilibrium?
8. How can an object be made more stable?
9. Besides manipulating the block's position, what other manipulation can you do within the simulation?
10. What are the key inquiry questions related to this simulation?

Quiz Answer Key

1. The key property is its ability to create a restoring torque that tends to return it to its original position. This is related to its stability.
2. The angular momentum of the object is conserved and the net torque acting on the object is zero.
3. The position of the center of gravity greatly affects the object's stability: if it's within the base the object will return to its original position, and if it's outside the base the object will fall over.
4. If the center of gravity is dragged outside the surface area of the object, the block will fall over.
5. The moment of a force (or torque) = force x perpendicular distance from the pivot.
6. The lever is one simple machine where the moment of a force is used.
7. For a body to be in rotational equilibrium, the sum of its clockwise moments about any point must be equal to the sum of anticlockwise moments about the same point.
8. An object can be made more stable by lowering its center of gravity or increasing its base area.
9. You can also change the width and height (resize) of the block within the simulation.
10. The key inquiry questions are "What are the characteristics and effects of forces in nature?" specifically addressing "Turning effects of forces," "Equilibrium of forces," "Centre of gravity," and "Stability."

Essay Questions

1. Discuss how the concepts of torque, center of gravity, and stability are interconnected in the rotating rectangular block simulation. Explain how changes to the block's position and dimensions affect these properties.
2. Analyze the role of the Principle of Moments in determining whether the rectangular block in the simulation will remain upright or topple. Describe a real-world scenario where the application of this principle is critical for stability.
3. Explore how the rotating rectangular block simulation can be used as an educational tool to help students understand the turning effects of forces and the concept of equilibrium. Discuss how the interactive nature of the simulation can aid in conceptual learning.
4. Compare and contrast the effects of adjusting the center of gravity versus adjusting the base area of the block, in terms of impact on its stability. Provide examples of how these principles are applied in real-world design for enhanced stability.
5. Evaluate the advantages and limitations of using the JavaScript HTML5 applet simulation for learning about rotational mechanics, comparing its utility with traditional learning methods for this subject.

Glossary of Key Terms

Angular Displacement: The change in the angle of an object during rotation.

Center of Gravity: The single point where the weight of an object can be considered to act.

Clockwise Moment: The turning effect of a force that tends to rotate an object in the clockwise direction.

Counterclockwise (Anticlockwise) Moment: The turning effect of a force that tends to rotate an object in the counterclockwise direction.

Equilibrium (Rotational): A state where the sum of all clockwise moments equals the sum of all counterclockwise moments about a point, resulting in no rotational acceleration.

Moment of a Force (Torque): A measure of the turning effect of a force, calculated by multiplying the force by the perpendicular distance from the pivot point.

Principle of Moments: The principle stating that for an object to be in rotational equilibrium, the sum of the clockwise moments must equal the sum of the counterclockwise moments about any point.

Restoring Torque: A torque that tends to return an object to its original position after it has been displaced.

Rotational Mechanical Equilibrium: The state where the angular momentum of an object is conserved and the net torque is zero.

Stability: A measure of a body's ability to maintain its original position and resist being displaced, often related to the position of its center of gravity and its base area.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.blocktiltapp658507

Introduction

Property of a body for which a small angular displacement set up a restoring torque that tends to return the body to its original position. In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. An important property of systems at mechanical equilibrium is their stability.

Instruction

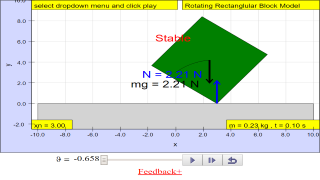
Drag the center of the block to make the block tilt with an angle. As long as the center of gravity stay inside the surface area of the object on the ground, the block will not fall out. Because the torque will always turn it back.
However, if the center of gravity was outside the surface area, the block will fall out.! You can also change width or height (resize) of the block within the simulation.

Key inquiry question: What are the characteristics and effects of forces in nature? 4. & 6. Turning effects of forces and Equilibrium of forces

• The moment of a force (or torque) = force x perpendicular distance from the pivot. The moment of a force is used in simple machines like the lever.

• Principle of moments states that for a body to be in rotational equilibrium, the sum of its clockwise moments about any point is equal to the sum of anticlockwise moments about the same point.

Key inquiry question: What are the characteristics and effects of forces in nature? 5 Centre of gravity and Stability

• The weight of a body may be taken as acting at a single point known as its centre of gravity; the position of which affects the stability of the body.

• Stability is a measure of a body’s ability to maintain its original position. Objects may be made more stable by lowering its centre of gravity or increasing its base area.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

 How to Teach using Simulation Full HD video by Joseph Chua Pei Hwa Sec

 

 How to Teach using Simulation part 1/2 by Joseph Chua Pei Hwa Sec

 Video showing how to use effect of forces for mouse trap design

https://youtu.be/ABffYDM9EwU

 How to Teach using Simulation part 2/2 by Joseph Chua Pei Hwa Sec

 Version:

1. http://weelookang.blogspot.sg/2016/03/rotating-rectangular-block-model.html a remix by lookang
   
2. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=433.0 original Java simulation by Fu-Kwun Hwang

Other Resources

https://www.geogebra.org/m/xmx55cj5 by seng kwang

https://ggbm.at/qszfx35k by tan seng kwang

https://ggbm.at/sw3txavd by Vincent Lew and tan seng kwang

Frequently Asked Questions: Rotating Rectangular Block Simulation

1. What is the primary concept demonstrated by the rotating rectangular block simulation? The simulation demonstrates the principles of rotational mechanical equilibrium and stability. Specifically, it explores how the position of a body's center of gravity relative to its base affects its stability. A restoring torque is generated when there is a small angular displacement which will bring it back to it's original position. If the center of gravity falls outside of the base of support, the object will topple.
2. How does the simulation allow users to interact with the block's stability? Users can interact with the simulation by dragging the center of the block, causing it to tilt. The simulation also allows for resizing of the block, altering its dimensions and thus the center of gravity. By observing the block's behavior as the center of gravity shifts, users can witness firsthand how the center of gravity affects a body's stability. If the center of gravity moves beyond the base, the block will fall due to the change in torque.
3. What does the simulation teach about the relationship between the center of gravity and stability? The simulation clearly shows that if the center of gravity of the rectangular block remains within its base area, the block will return to its original stable position after being tilted. However, if the center of gravity moves outside the base, the block will topple over. This visually demonstrates that a lower center of gravity and/or a larger base area increase an object’s stability.
4. What is torque, and how does it relate to the rotating block simulation? Torque, also known as the moment of a force, is the turning effect of a force. In this simulation, torque is caused by the force of gravity acting on the block's center of gravity. When the block is tilted, the torque either acts to restore the block to its original position or causes it to fall, depending on the center of gravity's position relative to the base of the block. The magnitude of this torque is based on the force of gravity and the perpendicular distance between the pivot point and the line of action of the gravity force.
5. What is the principle of moments, and how does it relate to the stability of the block? The principle of moments states that for a body to be in rotational equilibrium, the sum of the clockwise moments about a point is equal to the sum of the anticlockwise moments about the same point. In the context of the block, when the block is stable, the moments due to the force of gravity are balanced. When the block is tilted and unstable, the net moment due to gravity causes it to rotate.
6. How can this simulation be used in an educational setting? This simulation serves as a valuable tool to visually explore the concepts of rotational equilibrium, center of gravity, stability, and torque. It allows students to interactively manipulate variables, observe the effects of their actions, and develop a deeper understanding of physics principles that are often abstract. The provided video resources also demonstrate classroom application of this simulation.
7. What are the different platforms on which the simulation can be used? The simulation, built using JavaScript and HTML5, is accessible on various platforms including Windows, MacOSX, Linux, Chromebook laptops, and Android/iOS devices (including tablets, iPads and handphones). The embed code provided also allows it to be easily integrated into a web page.
8. What other resources are connected to this simulation, and what other related topics can be explored? The provided resources include other simulations such as other mechanics simulations, interactive GeoGebra models, simulations on energy and force, physics tracker modelling, and various teaching resources. This simulation is connected to other similar topics like moments, levers and principles of moments. A variety of other topics involving mechanical and rotational physics are linked to the page.