About

Topics

Measurement of length and time

Description

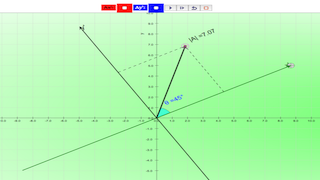
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical,

Calculate the components of the vector A in x' and y' direction

1. rotate the x' axis by dragging the GREEN slider to the 2 perpendicular direction to be resolved.
2. change the vector A to be resolved by dragging the BLACK |A| slider and the CYAN angle slider.
3. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x' axis.
4. use the formula Ax' = |A|cos(theta) to find the x' direction component Ax.
5. use the formula Ay' = |A|sin(theta) to find the y' direction component Ay.
6. click reset to random generate a new vector A.
7. test yourself whether you have enough practice calculating Ax' and Ay'.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 53 degrees. Select the checkboxes Ax' and Ay' to see the new answers.
2. when Ax' is selected, the PLAY button animates the effects of changing Ax' alone.
3. when Ay' is selected, the PLAY button animates the effects of changing Ay' alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.com/2014/10/decomposition-of-vector-advance-model.html

Sample Learning Goals

(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each

Version:

1. http://weelookang.blogspot.com/2014/10/decomposition-of-vector-advance-model.html
2. 
   

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

 http://iwant2study.org/lookangejss/01_measurement/ejss_model_horizontalverticalsincos/horizontalverticalsincos_Simulation.xhtml

Learning Objectives: https://sites.google.com/moe.edu.sg/a-level-physics-tlg/foundations-of-physics/quantities-measurement

Learning Outcomes: H2 - 1(h)(i)(j)

Curriculum Emphasis: Ways of Thinking and Doing [WOTD] https://vle.learning.moe.edu.sg/mrv/moe-library/lesson/view/c788167e-5865-4166-b147-89330b50b6b2/cover  SLS lesson includes questions that can be repeated indefinitely with random values inserted.

Versions:

1. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=634.0 sine and cosine by Fu-Kwun Hwang

 

Vector Decomposition Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences.

1. What is a vector, and how is it different from a scalar?
2. Provide two examples of physical quantities that are vectors.
3. What is the purpose of decomposing a vector?
4. Explain the role of trigonometry in vector decomposition.
5. How can you determine the magnitude of the horizontal component of a vector?
6. How can you determine the magnitude of the vertical component of a vector?
7. Why might you choose to resolve a vector into components that are not horizontal and vertical?
8. If a vector is resolved into two perpendicular components, what is the relationship between the magnitude of the original vector and the magnitudes of its components?
9. Describe how the applet simulation can help you understand vector decomposition.
10. Explain one "interesting fun activity" suggested in the source material that utilizes the applet simulation.

Answer Key

1. A vector is a quantity that has both magnitude (size) and direction, while a scalar has only magnitude. For example, speed is a scalar, while velocity is a vector.
2. Two examples of vector quantities are displacement (change in position with direction) and force (a push or pull with a specific direction).
3. Decomposing a vector breaks it down into two or more component vectors along specific axes. This simplifies calculations, especially when dealing with multiple vectors acting at different angles.
4. Trigonometric functions (sine, cosine, tangent) are used to calculate the magnitudes of the component vectors based on the angle and magnitude of the original vector.
5. The magnitude of the horizontal component is calculated by multiplying the magnitude of the original vector by the cosine of the angle it makes with the horizontal axis.
6. The magnitude of the vertical component is calculated by multiplying the magnitude of the original vector by the sine of the angle it makes with the horizontal axis.
7. Resolving a vector into components that are not horizontal and vertical might be useful when dealing with inclined planes or when analyzing motion along a curved path.
8. The magnitude of the original vector is the hypotenuse of a right triangle formed by the two component vectors. The Pythagorean theorem relates the magnitudes: the square of the original vector's magnitude equals the sum of the squares of the component magnitudes.
9. The applet allows users to visually manipulate a vector and its components, observing how changing the angle and magnitude of the vector affects its components in real-time. This interactive visualization enhances understanding of the relationship between a vector and its resolved parts.
10. One "interesting fun activity" is to use the applet to calculate the horizontal and vertical components of a vector for a specific magnitude and angle. By inputting the values and selecting the checkboxes for Ax' and Ay', the user can instantly see the calculated components.

Essay Questions

1. Discuss the importance of understanding vector decomposition in physics and engineering. Provide specific examples of how this concept is applied in real-world situations.
2. Explain the process of resolving a vector into two perpendicular components. Include a diagram and relevant equations in your explanation.
3. Compare and contrast the process of resolving a vector into horizontal and vertical components with resolving it into components along any two perpendicular axes. Explain the advantages and disadvantages of each approach.
4. Describe how you would use the applet simulation to teach a student about vector decomposition. Outline specific activities and learning objectives.
5. A ball is launched at an angle of 30 degrees above the horizontal with an initial velocity of 20 m/s. Using vector decomposition, analyze the motion of the ball. Determine the horizontal and vertical components of its initial velocity, and discuss how these components change over time.

Glossary of Key Terms

• Vector: A quantity with both magnitude and direction. Examples include displacement, velocity, acceleration, and force.
• Scalar: A quantity with only magnitude. Examples include speed, distance, mass, and temperature.
• Vector Decomposition: The process of breaking down a vector into two or more component vectors along specific axes.
• Component Vector: A vector that represents a part of the original vector along a specific axis.
• Magnitude: The size or length of a vector, represented by a numerical value.
• Direction: The orientation of a vector in space, often represented by an angle relative to a reference axis.
• Trigonometry: The branch of mathematics that deals with the relationships between the angles and sides of triangles, used in vector decomposition to calculate component magnitudes.
• Sine (sin): A trigonometric function that relates the opposite side of a right triangle to its hypotenuse.
• Cosine (cos): A trigonometric function that relates the adjacent side of a right triangle to its hypotenuse.
• Horizontal Component: The component of a vector that lies along the horizontal axis.
• Vertical Component: The component of a vector that lies along the vertical axis.
• Applet Simulation: An interactive computer program that visually represents and allows manipulation of a concept, such as vector decomposition.

Briefing Doc: Decomposition of Vectors in Non-Horizontal and Vertical Axes

Source: Excerpts from "Decomposition of (invariant or moving along axis) Vector along any 2 perpendicular axis Advance JavaScript HTML5 Applet Simulation Model" on Open Educational Resources / Open Source Physics @ Singapore website.

Main Theme: This source describes an interactive simulation designed to teach students about the decomposition of vectors along any two perpendicular axes, not just the standard horizontal and vertical axes.

Most Important Ideas/Facts:

• Vector Decomposition: A vector can be broken down into two or more component vectors that, when added together, result in the original vector. This is especially useful when dealing with vectors that are not aligned with the standard x and y axes.
• Non-Horizontal/Vertical Axes: This simulation specifically focuses on resolving vectors along axes that are not necessarily horizontal and vertical. This is important because in real-world scenarios, vectors often operate in directions that are not aligned with these standard axes.
• Applications: Understanding vector decomposition is crucial in various fields, including physics, engineering, and computer graphics. It allows for the analysis and manipulation of forces, motion, and other vector quantities in complex systems.

Key Features of the Simulation:

• Interactive Exploration: Users can manipulate the vector's magnitude and direction, as well as the orientation of the axes, using sliders.
• Visual Representation: The simulation visually displays the vector and its components, helping students grasp the concept of decomposition.
• Formula Application: The simulation encourages the use of trigonometric formulas (Ax' = |A|cos(theta) and Ay' = |A|sin(theta)) to calculate the components of the vector.
• Learning Objectives: The simulation aims to help students:
• Understand the concept of scalar and vector quantities.
• Learn how to resolve vectors into components along any two perpendicular axes.

Quotes:

• "What if the customary x-y coordinate axes is not (horizontal) and (vertical)? Sometimes, it could be useful to resolve vectors along and perpendicular to a slope, direction of travel than always horizontal and vertical." This highlights the importance of moving beyond the standard horizontal and vertical axes.
• "This model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 53 degrees. Select the checkboxes Ax' and Ay' to see the new answers." This showcases the interactive nature of the simulation and its ability to provide immediate feedback to the user.

Overall, this simulation provides a valuable tool for students to learn and explore the concept of vector decomposition in a more generalized and applicable manner.

Video

https://notebooklm.google.com/notebook/896dcf82-fab8-4d3f-8813-af73bab91726/audio

Other Resources

 

Vector Decomposition FAQ

1. What is a vector?

A vector is a mathematical quantity that represents both magnitude (size) and direction. Examples of vectors include displacement, velocity, acceleration, and force.

2. What is vector decomposition?

Vector decomposition is the process of breaking down a single vector into two or more component vectors that, when added together, result in the original vector. These component vectors are typically chosen to be perpendicular to each other, aligning with coordinate axes.

3. Why decompose vectors?

Decomposing vectors simplifies analysis and calculations, especially when dealing with vectors at angles to the standard horizontal and vertical axes. By resolving a vector into components, we can apply simpler mathematical tools to each component separately.

4. How to decompose a vector along any two perpendicular axes?

1. Choose your axes: Select two perpendicular axes (x' and y') along which you want to decompose the vector.
2. Determine the angle: Find the angle (theta) between the vector and one of the chosen axes.
3. Calculate components: Use the following formulas to calculate the components of the vector along each axis:

• x' component: Ax' = |A| * cos(theta)
• y' component: Ay' = |A| * sin(theta)
• Where:
• |A| represents the magnitude of the original vector.
• cos(theta) and sin(theta) are the cosine and sine of the angle, respectively.

5. Can we decompose vectors without using horizontal and vertical axes?

Yes, you can decompose vectors along any two perpendicular axes, not just the horizontal and vertical ones. This is useful when analyzing motion along a slope or in situations where other directions are more relevant.

6. What are some practical applications of vector decomposition?

Vector decomposition is used in various fields, including:

• Physics: Analyzing forces, motion, and projectiles.
• Engineering: Designing structures, calculating stress and strain.
• Computer graphics: Simulating motion and creating realistic animations.
• Navigation: Determining direction and speed of travel.

7. What is the significance of the sine and cosine functions in vector decomposition?

The sine and cosine functions relate the angle between the vector and the axes to the magnitudes of the component vectors. They provide the ratios needed to calculate the length of each component.

8. Are there any online tools available to help with vector decomposition?

Yes, interactive simulations and applets like the one mentioned in the source material can be used to visualize and experiment with vector decomposition. These tools allow users to manipulate vectors and axes, observe the resulting components, and reinforce their understanding of the concept.