About

Topics

Measurement of length and time

Description

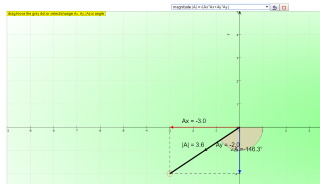
A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

Calculate the components of the vector A

1. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis.
2. use the formula Ax = |A|cos(theta) to find the x direction component Ax.
3. use the formula Ay = |A|sin(theta) to find the y direction component Ay.
4. click reset to random generate a new vector A.
5. test yourself whether you have enough practice calculating Ax and Ay.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees. Select the checkboxes Ax and Ay to see the new answers.
2. when Ax is selected, the PLAY button animates the effects of changing Ax alone.
3. when Ay is selected, the PLAY button animates the effects of changing Ay alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc here http://weelookang.blogspot.sg/2014/10/components-vector-model.html

Sample Learning Goals

(e) state what is meant by scalar and vector (how to resolve) quantities and give common examples of each

Version:

1. http://weelookang.blogspot.sg/2014/10/components-vector-model.html
2. 
   

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/01_measurement/ejss_model_horizontalvertical/horizontalvertical_Simulation.xhtml

Learning Objectives: https://sites.google.com/moe.edu.sg/a-level-physics-tlg/foundations-of-physics/quantities-measurement

Learning Outcomes: H2 - 1(h)(i)(j)

Curriculum Emphasis: Ways of Thinking and Doing [WOTD] https://vle.learning.moe.edu.sg/mrv/moe-library/lesson/view/c788167e-5865-4166-b147-89330b50b6b2/cover  SLS lesson includes questions that can be repeated indefinitely with random values inserted.

Topics

Measurement of length and time

Vectors and Components Study Guide

Glossary of Key Terms

• Vector: A quantity that has both magnitude (size) and direction. Examples include displacement, velocity, acceleration, and force.
• Scalar: A quantity that has only magnitude, but no direction. Examples include mass, temperature, and speed.
• Magnitude: The size or length of a vector, often representing the strength of the quantity.
• Direction: The orientation of a vector, indicating where the quantity is pointing.
• Component: The projection of a vector onto a specific axis. A vector can be broken down into horizontal (x-component) and vertical (y-component) parts.
• Resolution of Vectors: The process of breaking down a vector into its components along specific axes.
• Horizontal Component (Ax): The projection of a vector onto the x-axis, representing the magnitude of the vector in the horizontal direction.
• Vertical Component (Ay): The projection of a vector onto the y-axis, representing the magnitude of the vector in the vertical direction.
• Angle (θ): The angle between a vector and a reference axis, usually measured counterclockwise from the positive x-axis.
• Trigonometric Functions: Mathematical functions (sine, cosine, tangent) used to relate the angle of a vector to its components and magnitude.

Quiz

1. What is the difference between a scalar and a vector quantity? Provide an example of each.
2. Describe the concept of vector resolution. Why is it useful in physics?
3. Given a vector with a magnitude of 10 units and an angle of 30 degrees with respect to the positive x-axis, how would you calculate its horizontal and vertical components?
4. Explain the relationship between the magnitude of a vector and the magnitudes of its components.
5. If you know the horizontal and vertical components of a vector, how can you determine the magnitude and direction of the original vector?
6. What are the trigonometric functions used in resolving vectors, and what do they represent in terms of the vector's components and angle?
7. Explain how the interactive applet simulation helps in understanding the concept of vector components.
8. What are some practical applications of vector resolution in real-world scenarios?
9. How does the understanding of vector components contribute to solving problems related to motion, forces, or other physical phenomena?
10. Can you give an example of a situation where resolving a vector into its components simplifies the analysis of a problem?

Answer Key

1. A scalar quantity has only magnitude, while a vector quantity has both magnitude and direction. Examples of scalar quantities are mass, temperature, and speed. Examples of vector quantities are displacement, velocity, and force.
2. Vector resolution is the process of breaking a vector down into its components along specific axes. This is useful in physics because it allows us to analyze the effects of a vector in different directions separately.
3. To calculate the components, we use the following formulas: Horizontal component (Ax) = Magnitude * cos(angle) = 10 units * cos(30°) ≈ 8.66 units Vertical component (Ay) = Magnitude * sin(angle) = 10 units * sin(30°) = 5 units
4. The magnitude of a vector is related to the magnitudes of its components using the Pythagorean theorem: Magnitude² = Horizontal component² + Vertical component².
5. If you know the horizontal and vertical components, you can calculate the magnitude using the Pythagorean theorem and the direction using the arctangent function: Angle = arctan(Vertical component / Horizontal component).
6. The trigonometric functions used are sine, cosine, and tangent. Sine (sin θ) = Opposite side / Hypotenuse = Vertical component / Magnitude Cosine (cos θ) = Adjacent side / Hypotenuse = Horizontal component / Magnitude Tangent (tan θ) = Opposite side / Adjacent side = Vertical component / Horizontal component
7. The applet simulation allows users to visualize the process of resolving vectors into components. By manipulating the magnitude and direction of a vector, users can observe how the corresponding components change. This interactive experience helps solidify the understanding of the relationships between vectors, components, and angles.
8. Vector resolution is applied in various fields like navigation, engineering, and sports. For example, in analyzing the motion of a projectile, resolving its velocity into horizontal and vertical components helps determine its range, time of flight, and maximum height. In structural engineering, forces acting on a beam are resolved into components to calculate stresses and strains.
9. Understanding vector components helps break down complex problems into simpler ones by analyzing the effects of forces or motion in different directions independently. This is crucial in solving problems related to equilibrium, kinematics, and dynamics.
10. Consider a ball rolling down an inclined plane. Resolving the gravitational force acting on the ball into components parallel and perpendicular to the incline helps determine the ball's acceleration down the slope and the normal force acting on it. This simplifies the analysis of the ball's motion.

Essay Questions

1. Explain the importance of vector resolution in physics, providing at least three distinct examples where this concept is applied to solve problems.
2. Discuss the relationship between the magnitude of a vector, the magnitudes of its components, and the angle the vector makes with a reference axis. Include relevant equations and diagrams.
3. Describe the steps involved in calculating the horizontal and vertical components of a vector, given its magnitude and direction. Illustrate the process with an example.
4. Explain how the interactive applet simulation enhances the understanding of vector components. What are the benefits of using such simulations in learning and teaching physics concepts?
5. Discuss the limitations of resolving vectors in two dimensions. Why is it sometimes necessary to consider three-dimensional vector resolution, and how does this process differ from the two-dimensional case?

Description

A vector is a quantity that has both magnitude and direction. Displacement, velocity, acceleration, and force are the vector quantities. in simpler examples, vectors were simply directed up, down, left or right. In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

Briefing Doc: Resolving Vectors into Components

Source: Excerpts from "Component of a Vector or Sine and Cosine Components JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore | Open Educational Resources / Open Source Physics @ Singapore"

Main Themes:

• Vectors and their Components: This source focuses on explaining the concept of vectors, their representation, and how to decompose them into horizontal (x) and vertical (y) components using trigonometry.
• Applications in Physics: The source highlights the importance of vectors in physics, mentioning examples like displacement, velocity, acceleration, and force.
• Interactive Learning: The document describes an interactive JavaScript model that allows students to visualize vector decomposition and practice calculating components.

Most Important Ideas/Facts:

• Definition of a Vector: "A vector is a quantity that has both magnitude and direction."
• Examples of Vectors: Displacement, velocity, acceleration, and force.
• Vector Decomposition: Vectors can be broken down into components along the x and y axes. This simplifies calculations, especially when dealing with vectors at an angle to the coordinate axes.
• Calculating Components:x-component: Ax = |A| cos(θ)
• y-component: Ay = |A| sin(θ) where |A| is the magnitude of the vector and θ is the angle it makes with the positive x-axis.
• Interactive Model: The described JavaScript model provides a visual and interactive way to learn about:
• Generating random vectors
• Calculating components
• Observing the effects of changing component values.

Key Quotes:

• "In situations in which vectors are directed at angles to the customary x(horizontal)-y(vertical) coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes."
• "A vector that is directed northwest can be thought of as having two parts - a northward part and a westward part."
• "This model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees."

Educational Value:

The source presents a clear and concise explanation of vector components. The interactive model is a valuable tool for promoting student engagement and deeper understanding of the topic. It allows for experimentation and visualization, which can significantly enhance learning.

Engage:

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has magnitude, has direction, and which adheres to the rules of vector addition. An example is velocity, the magnitude of which is speed. For example, the velocity 4 meters per second upward could be represented by the vector \( A_{y}\) = (0,4) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force, since it has a magnitude and direction and follows the rules of vector addition. Vectors also describe many other physical quantities, such as linear displacement, displacement, linear acceleration, angular acceleration, linear momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field. Examples of quantities that have magnitude and direction but fail to follow the rules of vector addition: Angular displacement and electric current. Consequently, these are not vectors.

Component:

As explained above a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set. For simplicity, let's assume x and y direction as the reference axes, referring to the model above.

the equations for the components are:

 \( A_{x} = A cos( \theta) \)

 \( A_{y} = A sin( \theta) \)

 

Model:

This model uses the following equations:

Length or Magnitude |A|:

The length or magnitude or norm of the vector a is denoted by |A|.

 \( |A| = \sqrt {( A_{x}^{2}+A_{y}^{2})} \)

Angle:

The angle in radian of the vector that makes with the positive x axis is

\( \theta = tan^{-1} (\frac {A_{y}}{A_{x}}) \)

the conversion to degree is

\( \theta_{degree} = (tan^{-1} (\frac{A_{y}}{A_{x}}) )( \frac{180}{\pi}) \)

or

\( \theta_{degree} = ( \theta )( \frac{180}{\pi}) \)

in the design of the slider values which shows in degree, the equation that converts back from degree to radian is used

\( \theta = ( \theta_{degree} )( \frac{\pi}{180}) \)

Calculate the components of the vector A

1. click reset to generate a new random vector A of length |A| at an angle of theta to the positive x axis.
2. use the formula Ax = |A|cos(theta) to find the x direction component Ax.
3. use the formula Ay = |A|sin(theta) to find the y direction component Ay.
4. click reset to random generate a new vector A.
5. test yourself whether you have enough practice calculating Ax and Ay.

Other interesting fun activities

1. this model can be used to calculate any length |A| by keying in the values such as |A| =500 and theta = 63 degrees. Select the checkboxes Ax and Ay to see the new answers. 
2. when Ax is selected, the PLAY button animates the effects of changing Ax alone.
3. when Ay is selected, the PLAY button animates the effects of changing Ay alone.
4. explore your own vector(s) here to test your understanding.
5. leave me a Google+ comment/question/requests etc herehttp://weelookang.blogspot.sg/2014/10/components-vector-model.html 

Sample Learning Goals

(e) state what is meant by scalar and vector(how to resolve) quantities and give common examples of each

 

Version:

1. http://weelookang.blogspot.sg/2014/10/components-vector-model.html

2. http://weelookang.blogspot.sg/2014/10/components-vector-model.html CLICK https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical/horizontalvertical_Simulation.xhtml author: lookang, Fu-Kwun, Andreu Glasmann, Wolfgang Christian, and Mario Belloni offline use: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_horizontalvertical.zip source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_horizontalvertical.zip author of EJS 5: Paco.

3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=662.0 Represent a vector as horizontal and vertical components applet by Loo Kang Wee and Fu-Kwun Hwang
4. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=661.0 Magnitude of a Vector by Loo Kang Wee and Fu-Kwun Hwang

 

Video

https://notebooklm.google.com/notebook/23e3a401-f3be-4d65-80c9-d4a26b632c8f/audio

Other Resources

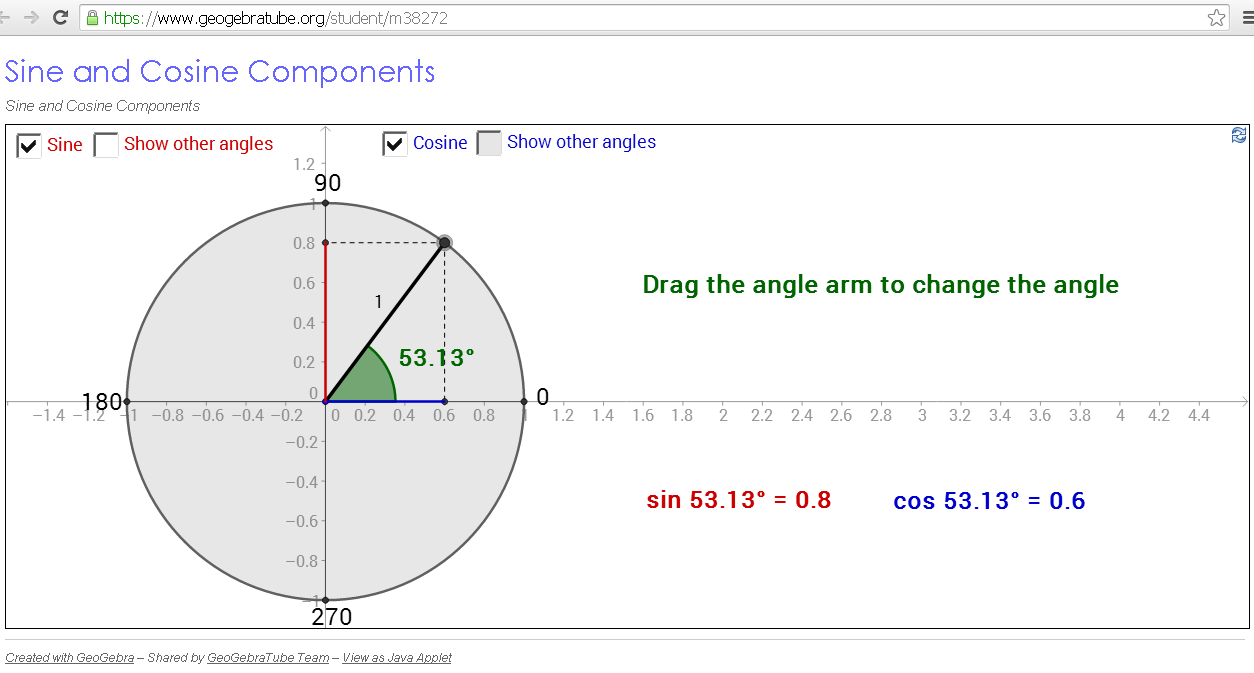
1. Example JavaScript Model Ill 3.1: Vector Decomposition written by Andreu Glasmann, Wolfgang Christian, and Mario Belloni 
2. https://www.geogebratube.org/student/m38272