About

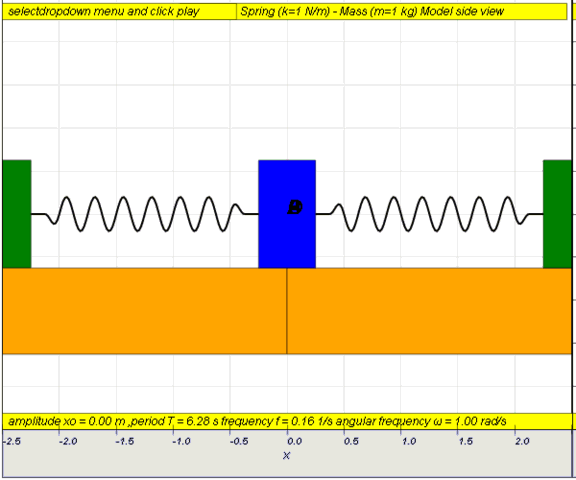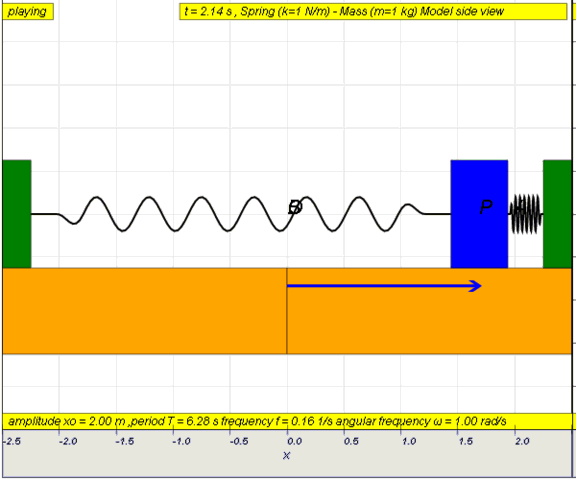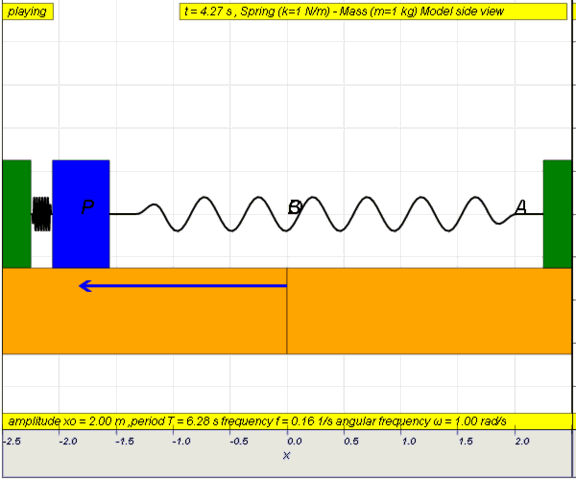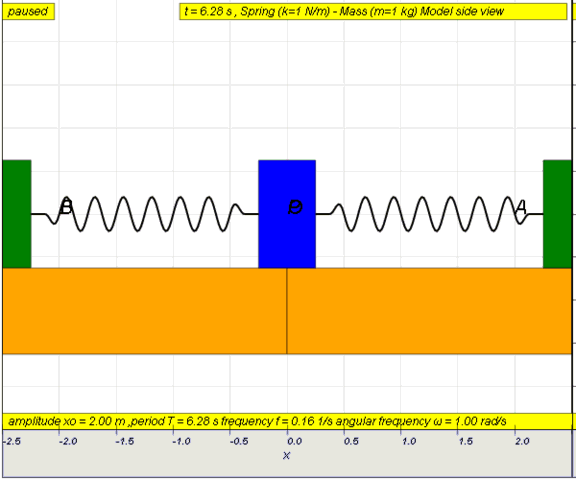
Simple Harmonic Motion

Guiding Questions

1. What are the characteristics of periodic motion? How can we study and describe such motion?
2. How can circular motion be related to simple harmonic motion (SHM)?
3. How do we analyse simple harmonic motion?

Learning Outcomes (LOs) 

1. describe simple examples of free oscillations.
2. investigate the motion of an oscillator using experimental and graphical methods.
3. understand and use the terms amplitude, period, frequency and angular frequency.
4. recognise and use the equation a =  - ω² x as the defining equation of simple harmonic motion.
5. recall and use x= x₀ ω sin( ωt )as a solution to the equation a =  - ω² x
6. recognise and use v = v₀ cos ( ω t )  , ${\displaystyle v=\pm \omega \sqrt{(x_0^2-x^2)}}$
7. describe with graphical illustrations, the changes in displacement, velocity and acceleration during simple harmonic motion.
8. describe the interchange between kinetic and potential energy during simple harmonic motion.
9. describe practical examples of damped oscillations with particular reference to the effects of the degree of damping and the importance of critical damping in cases such as a car suspension system.
10. describe practical examples of forced oscillations and resonance.
11. describe graphically how the amplitude of a forced oscillation changes with driving frequency near to the natural frequency of the system, and understand qualitatively the factors which determine the frequency response and sharpness of the resonance
12. show an appreciation that there are some circumstances in which resonance is useful and other circumstances in which resonance should be avoided.

Learning Experiences

1. Examine representations used in oscillations
   • Examine how different graphs are used to represent SHM. Draw links between the different graphs highlighting the positive and negative values and their interpretation. These will help students to understand SHM as a function of two variables (space and time) and understand the treatment of vector and scalar quantities .
2. Investigate factors affecting period of oscillations using experiments or a simulation
   • Design and carry out an experiment  to build a pendulum or spring-mass system to obtain a prescribed period. Present the experimental design, explaining the factors that determine the period of the oscillating system. This provides an opportunity for students to predict and collect data to ascertain the properties of a system and determine whether a motion is considered to be SHM. Students are also to understand that it is necessary for oscillations to be small for the motion to be considered as SHM. Students can also be shown other systems that demonstrate SHM . Simulations [1] [2] [3] ,  can also be used for students to investigate these factors.
3. Investigate phase using a turntable or a simulation
   • Investigate phase using a turntable  or a simulation  to associate each position in an SHM with a position on a uniform circular motion. This idea can be extended to the phase difference between different positions in an SHM. The association of SHM with uniform circular motion helps students to visualise many aspects of SHM. Students are to make mental links between three related ideas: physical position and velocity of the oscillator, angle in the associated uniform circular motion and the position of the oscillator on a displacement-time graph .
4. Build a model for SHM using a datalogger or simulation
   • Investigate the motion of a SHM system (pendulum, mass-spring system) using a datalogger  or a simulation . Students are to practice observing the motion and interpreting graphs before getting into the mathematical details of the equations. Compare the relationship between the different variables particularly note the values of these valuables at equilibrium position and at endpoints. Students should practice converting one graph into another.
5. Explore modelling of oscillation in molecules as SHM
   • Explore how oscillations of molecules bounded by the van der Waals interaction can be SHM if the amplitude is small [4] .
6. Explore benefits and danger of resonance
   • Explore various examples of resonance  and discuss the benefits  and dangers  of resonance.

1. Simple examples of free oscillations LO(a)

1.1 YouTube of many examples of oscillators

http://youtu.be/VKtEzKcg6_s This video can be used at the start of the first lecture (while students settle down for lecture) to introduce oscillations, to show various modes of oscillations and to interest them.

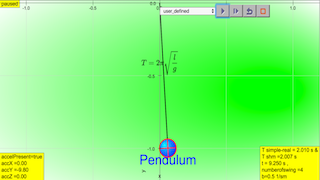
1.1.1 Example 1: Simple pendulum

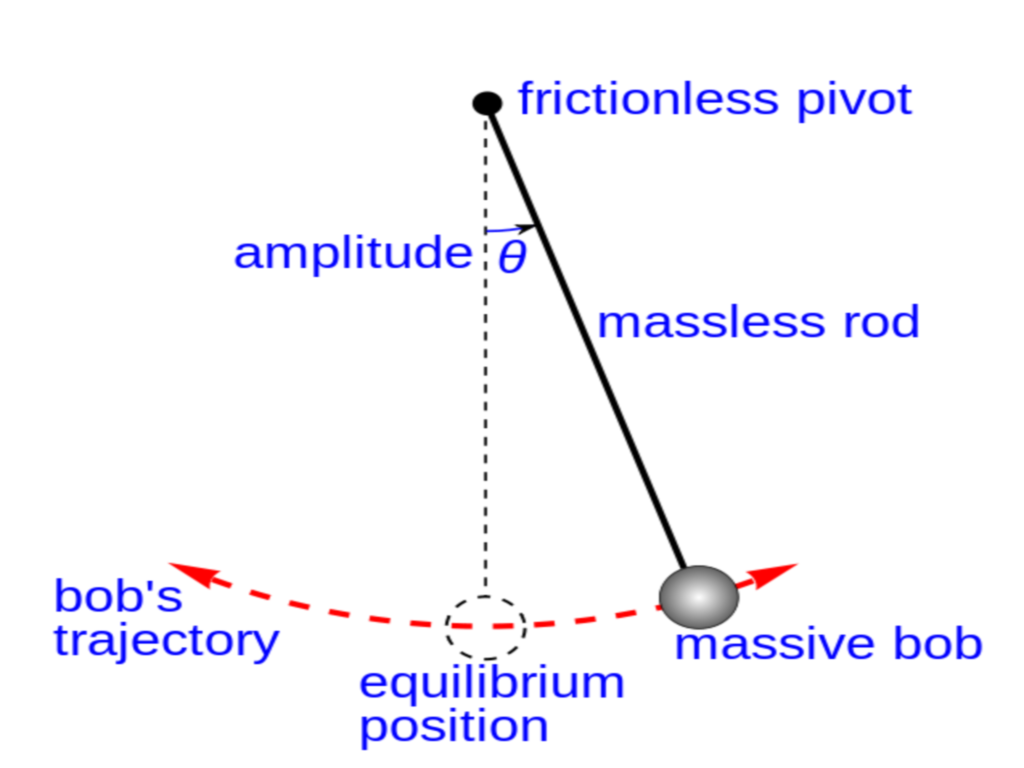
Static picture of a pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion

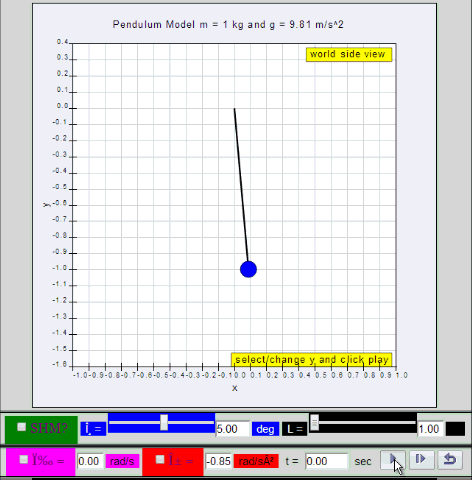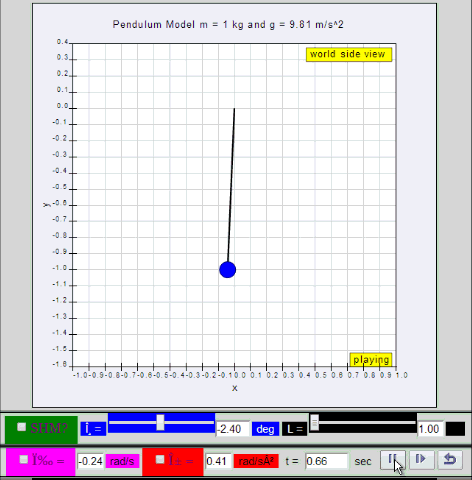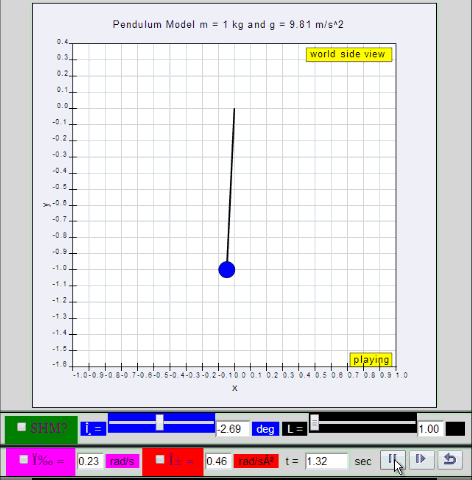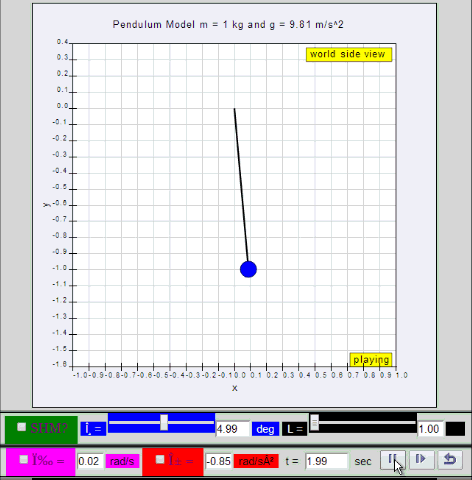
Dynamic picture of a pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion

1.1.2 Run Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/67

1.1.2.Q1: what is the maximum angle of release before the motion is not accurately described as a simple harmonic motion for the case of a simple free pendulum?

1.1.2.A1: : 10 degrees for error of , depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical.

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang; Francisco Esquembre; Wolfgang Christian; Flix J. Garca

 

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM01/SHM01_Simulation.xhtml

 

Briefing Document: ⚛️10 Pendulum JavaScript Model Simulation Applet HTML5

1. Overview

This document reviews the "10 Pendulum JavaScript Model Simulation Applet HTML5" resource from Open Educational Resources / Open Source Physics @ Singapore. This resource is designed as an interactive simulation tool and learning resource focused on simple harmonic motion (SHM), specifically using a pendulum model. It's intended for use across multiple educational levels from primary to junior college, supporting hands-on exploration and understanding of oscillatory motion. The resource leverages HTML5 and JavaScript for broad accessibility across various platforms (desktops, laptops, tablets, and smartphones).

2. Key Themes and Ideas

• Simple Harmonic Motion (SHM): The central focus is on understanding SHM through the lens of a pendulum. The resource aims to help learners understand the fundamental principles and characteristics of SHM, exploring its relationship with circular motion.
• Interactive Learning: This is a simulation-based approach, encouraging active engagement through experimentation and observation. The applet allows users to manipulate parameters and visualize the resulting effects on the pendulum’s motion.
• Graphical Representation: A significant emphasis is placed on understanding and interpreting graphs of displacement, velocity, and acceleration in SHM. Students are expected to recognize and interpret these graphs.
• Energy Transfer: The learning objectives include understanding the interchange between kinetic and potential energy during SHM.
• Damped and Forced Oscillations: The resource introduces damped oscillations and the concept of resonance, including practical examples such as car suspension systems.
• Exploration of Variables: The simulations facilitate investigating the effects of different factors like gravity, rod length, starting angle, and mass on the period of oscillation.
• Real-World Applications: The resource connects SHM to real-world phenomena including, damped oscillations in car suspension, forced oscillations and resonance, and even molecular oscillations (van der Waals interactions) with a link to research [4https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM01/SHM01_Simulation.xhtml " frameborder="0"></iframe>
• Guiding Questions: Prompts for student thought and exploration, such as: "What are the characteristics of periodic motion? How can we study and describe such motion?" "How can circular motion be related to simple harmonic motion (SHM)?"
• Experimentation and Manipulation: Users can manipulate variables in the simulation such as gravity, rod length, starting angle, and mass. They can also observe the impact of damping on the oscillations.
• Period Calculation: The simulator includes a graph that can be used to determine the period of the pendulum.
• Multiple Oscillator Systems: The resource includes a simulation for pendulums that move both back and forth and up and down, which can help students visualize more complex oscillatory phenomena.

6. Limitations and Considerations

• Small Angle Approximation: The resource specifies that for accurate SHM representation, the pendulum's angle of release should be "less than 10 degrees...depending on what is the error acceptable."
• Simulation Focus: The resource focuses heavily on the simulation itself, with links provided to other supplementary online resources for additional exploration.
• Error Calculation: The small angle approximation depends on what is considered an "acceptable error".

7. Additional Resources

The document points towards additional resources, including:

• YouTube Video: A video showcasing various modes of oscillations (http://youtu.be/VKtEzKcg6_s).
• Other Simulations: Links to external pendulum simulations at websites like walter-fendt.de, physics.bu.edu, phet.colorado.edu and thephysicsaviary.com.
• GeoGebra Applet: A resource on the Conical Pendulum (https://www.geogebra.org/m/sux2Q5ak).
• App: A link to an Android app: (https://play.google.com/store/apps/details?id=com.ionicframework.shm01app615913&hl=en)

8. Conclusion

The "10 Pendulum JavaScript Model Simulation Applet HTML5" is a comprehensive, interactive educational tool for exploring Simple Harmonic Motion. Its strength lies in its combination of simulation-based experimentation, strong focus on graphical representation, and its wide accessibility, all of which promote an active learning environment. The stated objectives and learning experiences make it a valuable resource for students of varying educational levels.

Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is periodic motion and what are some of its characteristics?
2. Explain the relationship between circular motion and simple harmonic motion (SHM).
3. What is the defining equation of SHM, and what do the variables represent?
4. Define amplitude, period, and frequency in the context of SHM.
5. Describe the energy transformations that occur during simple harmonic motion.
6. Explain the concept of damped oscillations and provide a practical example.
7. What are forced oscillations, and how does resonance occur?
8. How does damping affect the period of a pendulum?
9. What is the maximum release angle for a pendulum to exhibit SHM?
10. Why is it important for oscillations to be small for motion to be considered SHM?

Quiz Answer Key

1. Periodic motion is motion that repeats itself at regular intervals. Some of its characteristics include a consistent period, frequency, and amplitude.
2. Simple Harmonic Motion can be understood as the projection of circular motion onto a single axis. The back-and-forth motion of an SHM system corresponds to a point moving around a circle.
3. The defining equation of SHM is a = -ω²x, where ‘a’ represents acceleration, ‘ω’ is the angular frequency, and ‘x’ is the displacement from the equilibrium position.
4. Amplitude is the maximum displacement from the equilibrium position, the period is the time it takes for one complete oscillation, and frequency is the number of oscillations per unit time.
5. During SHM, there is a continuous interchange between kinetic and potential energy. At the extremes of motion, the energy is all potential, and at the equilibrium position, it is all kinetic.
6. Damped oscillations are oscillations where energy is gradually lost over time, causing the amplitude of the motion to decrease. A practical example is the suspension system of a car.
7. Forced oscillations occur when an external force is applied to an oscillating system. Resonance occurs when the driving frequency of the external force matches the natural frequency of the system.
8. Ideally, damping does not change the period of a pendulum for simple harmonic motion, but it does reduce the amplitude of the oscillations.
9. The maximum release angle for a pendulum to accurately exhibit SHM is approximately 10 degrees, depending on acceptable error.
10. For oscillations to be considered SHM, they must be small in amplitude because the restoring force must be proportional to the displacement, a condition that only holds true for small angles in a pendulum.

Essay Questions

Instructions: Answer the following essay questions with a well-organized, multi-paragraph response.

1. Discuss the significance of understanding Simple Harmonic Motion in various fields of science and engineering. Provide examples where SHM plays a critical role.
2. Compare and contrast damped and forced oscillations. Explain the factors that affect each and discuss the implications of each in real-world scenarios.
3. Describe an experiment you might design to investigate the factors that affect the period of a pendulum, highlighting both the methodology and the expected results.
4. Using graphical representations, explain the relationships between displacement, velocity, and acceleration in SHM. Include the use of sine and cosine graphs and discuss how they relate to one another.
5. Explain the relationship between Simple Harmonic Motion and energy conservation. What types of energy are involved, and how is energy transformed during SHM?

Glossary of Key Terms

Amplitude: The maximum displacement of an oscillating object from its equilibrium position.

Angular Frequency (ω): A measure of the rate of oscillation, typically in radians per second, related to the frequency by ω = 2πf.

Damped Oscillations: Oscillations where the amplitude decreases over time due to energy dissipation.

Displacement (x): The distance and direction of an object from its equilibrium position.

Forced Oscillations: Oscillations that are driven by an external force.

Frequency (f): The number of complete oscillations or cycles that occur per unit time, measured in hertz (Hz).

Kinetic Energy: The energy of motion. In SHM, kinetic energy is maximum at the equilibrium position.

Oscillation: A single instance of motion of an object back and forth between two positions.

Period (T): The time it takes for one complete oscillation to occur, measured in seconds.

Potential Energy: Stored energy that has the potential to do work. In SHM, potential energy is maximum at the extremes of motion.

Resonance: The phenomenon where the amplitude of an oscillation increases dramatically when the driving frequency matches the natural frequency of the system.

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction to the displacement.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm01app615913&hl=en

Video

https://notebooklm.google.com/notebook/647ab3d5-26d0-4862-95cd-156aaa0ae835/audio

Other Resources

1.  https://www.geogebra.org/m/sux2Q5ak The Conical Pendulum by ukukuku

 

1. http://www.walter-fendt.de/html5/phen/pendulum_en.htm 
2. http://physics.bu.edu/~duffy/HTML5/pendulum.html
3. https://phet.colorado.edu/en/simulation/pendulum-lab 
4. http://www.thephysicsaviary.com/Physics/Programs/Labs/PendulumLab/index.html

Timeline of Events (Implied and Explicit)

• Pre-2024: Development of the Easy JavaScript Simulation (EJS) authoring toolkit. This is implied by the repeated references to webEJS and EJS simulations. This tool allows for the creation of interactive physics simulations for educational use. The tool was created by the people below.
• Ongoing/2024: The creation and deployment of the "10 Pendulum JavaScript Model Simulation Applet HTML5". This resource is designed to teach Simple Harmonic Motion (SHM) concepts, and is available for use in primary, secondary, and junior college settings. It's compatible with various platforms, including computers and mobile devices. The dates of workshops also suggest this is an ongoing project.
• Early 2024: WebEJS beta Workshop run by Francisco Esquembre and Félix J. García Clemente.
• 2024: Various project and training workshops related to WebEJS take place throughout the year.
• Ongoing: Active development and sharing of various WebEJS projects, simulations and teaching resources by various people, demonstrating the ongoing nature of the project and its resources.
• Ongoing: Students use the pendulum simulation and other resources for learning about SHM and related physics concepts. They conduct experiments, analyze graphs, and explore concepts like amplitude, period, frequency, damping, resonance, and energy interchange. Students also use other simulations that may or may not be related to this specific simulation.
• Ongoing: Teachers and educators use the simulations and resources to enhance their instruction of physics and mathematics concepts, as evidenced by the projects and professional development activities described in the sources.
• 2024: The Open Educational Resources / Open Source Physics @ Singapore is currently live and actively providing resources.

Cast of Characters

• Fu-Kwun Hwang: A key developer involved in the creation of the EJS simulation and credited for the SHM model applet. Likely a physics educator and/or programmer.
• Francisco Esquembre: One of the key developers of EJS software (mentioned in the credits), which underpins all these simulations, and ran workshops for educators. Likely a programmer with expertise in simulations.
• Wolfgang Christian: Another key developer of EJS, also a well known name in physics open source resources. Likely a physics professor involved in creating open educational physics resources.
• Félix J. García Clemente: Another key developer of the underlying EJS software and ran workshops for educators. Likely a programmer with expertise in simulations.
• lookang: The listed user for this website and the creator of the various listed materials. Likely an educator who curates and facilitates the use of the educational resources.

Frequently Asked Questions about Simple Harmonic Motion (SHM)

1. What defines periodic motion, and how can we study it? Periodic motion is any motion that repeats itself at regular intervals. To study this motion, we examine its characteristics, such as the time it takes for one complete cycle (period), the number of cycles per unit time (frequency), and the maximum displacement from equilibrium (amplitude). We can use experiments, graphs of displacement, velocity, and acceleration over time, and mathematical equations to describe and analyze periodic motion, like Simple Harmonic Motion (SHM).
2. How is circular motion related to Simple Harmonic Motion (SHM)? SHM can be understood as the projection of uniform circular motion onto a single axis. Imagine a point moving in a circle; its shadow projected onto a horizontal or vertical line will move back and forth in SHM. This relationship helps visualize SHM, particularly in terms of phase, velocity, and position. The angle in circular motion corresponds to the phase of SHM.
3. What is the defining equation of Simple Harmonic Motion, and what does it mean? The defining equation of SHM is a = -ω²x, where a is the acceleration, x is the displacement from the equilibrium position, and ω (omega) is the angular frequency. The negative sign indicates that the acceleration is always directed towards the equilibrium position, and the equation implies that the acceleration is directly proportional to the displacement. In simpler terms, the further an object is from its resting position, the harder it is pulled back.
4. What are the key terms used to describe SHM, and how are they related? Key terms include amplitude, period, frequency, and angular frequency. Amplitude is the maximum displacement from equilibrium. Period (T) is the time taken for one complete oscillation. Frequency (f) is the number of oscillations per second and is the reciprocal of the period (f = 1/T). Angular frequency (ω) is related to the frequency by ω = 2πf. These terms are interconnected, and a change in one affects the others; for example, a higher frequency means a shorter period.
5. How do displacement, velocity, and acceleration change during Simple Harmonic Motion (SHM)? During SHM, the displacement, velocity, and acceleration are continually changing. When displacement is at a maximum (either positive or negative), the velocity is zero, and the acceleration is at its maximum but in the opposite direction to the displacement. At the equilibrium position, the displacement is zero, the velocity is at its maximum, and the acceleration is zero. These relationships are also shown in displacement-time, velocity-time, and acceleration-time graphs, and all three quantities oscillate, but with a phase difference among them.
6. How does energy interchange during Simple Harmonic Motion (SHM)? During SHM, there is a continuous interchange between kinetic and potential energy. When an oscillating object is at its maximum displacement (endpoints), its kinetic energy is zero, and its potential energy is at its maximum. Conversely, at the equilibrium position, its potential energy is zero, and its kinetic energy is at its maximum. The total energy of the system remains constant (assuming no damping), just shifting between these two forms.
7. What is damping, and what is its importance? Damping is the reduction in amplitude of oscillations over time due to energy dissipation, typically due to friction or air resistance. Damping can range from light to critical to overdamping. Critical damping is particularly important in systems like car suspension, where oscillations need to be reduced quickly and efficiently to ensure stability and comfort. Understanding and controlling the degree of damping is essential in many practical applications.
8. What are forced oscillations and resonance, and why are they significant? Forced oscillations occur when an external force causes an object to oscillate. Resonance happens when the driving frequency of the external force matches the natural frequency of the system, leading to a large amplitude of oscillation. Resonance can be beneficial in some situations, such as in musical instruments and tuned circuits, but it can be destructive in others, like in bridges or buildings during earthquakes. Knowing how to control resonance and design systems to avoid or make use of resonance is critical in various engineering and scientific contexts.