Breadcrumbs

About

Block On An Incline Plane

Note: When running this simulation on a tablet or smart-phone, set the parameters, then press the Play button. When running this simulation on a computer, be sure to check “No sensor,” then set the parameters and press the Play button.

Block On An Incline

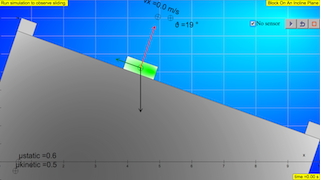
The Block Sliding On An Incline Plane mobile JavaScript model illustrates the forces and dynamics of a block sliding on a surface. This simulation uses the accelerometer on your mobile device to read the direction of the gravitation field g. You may need to lock the orientation of your screen to maintain a fixed view as you tilt your device. For use on computers without an accelerometer or for classroom use, the "No sensor" mode simulates a tilted device in the view.

A force body (free body) diagram showing the normal force (red), the gravitational force (black), and the force of friction (green) is shown. Users can set the initial position and velocity and can adjust both the static and kinetic coefficient of friction when the simulation is paused. Test your knowledge of incline plane dynamics by answering the following questions and comparing your answers with the simulation results. Remember to press the play button after you set the initial values.

Initial values, such as x₀ and v₀, can be set when the simulation is paused but not when the simulation is running. (Non-editable input fields have a grey background.) You may also drag the block when the simulation is paused. The reset button returns the system to its default state while the reset time button returns the system to the previous values of x₀ and v₀.

Physics Exercises:

Draw a force body diagram for a block on a horizontal surface (θ = 0°), labeling all forces.
Draw a force body diagram for a block on a surface inclined at an arbitrary nonzero angle of θ, labeling all forces.
The formula for the force of friction f when the block is not slipping is often given in textbooks as f = μ_sN where N is the magnitude of the normal force. But the simulation shows that the force of friction changes as the surface tilts. Explain why the force of friction is not constant.
What happens in the simulation if you set μ_s less than μ_k? Give a physical reason why the response is reasonable. What happens in the simulation if you set μ_s or μ_k less than zero? Give a physical reason why the response is reasonable.
Derive an expression for the maximum tilt angle without the block slipping (v_x= 0) when μ_s= {0.5, 0.6, 0.8, 1.0, 5.0}. Verify with the simulation. Note that the maximum allowed value of μ_s is five in this simulation.
The block is constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers. Suppose ϴ = 0°, and the block is given an initial speed, v = 3 m/s to the right. Derive an expression for how far the block will move. Verify with the simulation if the static coefficient of friction is μ_s= 0.5 and the kinetic coefficient of friction is μ_k= 0.4.
Suppose θ = -30°, and the block starts from rest at x = 1 (m) with a speed of 3 (m/s) up the incline. Derive an expression for how far the block moves up the incline. Verify with the simulation if μ_s= 0.6 and the kinetic coefficient of friction is μ_k= 0.4.
Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Will the block stop before it reaches the end bumper if μ_s= 0.6 and the kinetic coefficient of friction is μ_k= 0.4? If not, what is the speed when the block reaches the bumper. Derive an expression for the block to move at constant speed down the incline and verify with the simulation.
Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Derive a value for μ_k for the block to stop sliding just before it reaches the end bumper. Verify with the simulation.

Note: Because continuously reading the accelerometer may drain the battery on a mobile device, you must run the simulation to read the device tilt. The simulation will automatically pause after 4 minutes to conserve battery power.

Credits:

The Block Sliding On An Incline Plane mobile JavaScript model was developed by Wolfgang Christian using version 5 of the Easy Java Simulations (EJS 5) modeling tool. Although EJS is a Java program, EJS 5 creates stand alone JavaScript programs that run in almost any browser. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the AAPT-ComPADRE Open Source Physics collection <http://www.compadre.org/OSP/>.

Translations

Code	Language		Translator	Run

Credits

Wolfgang Christian; Loo Kang Wee

http://iwant2study.org/lookangejss/02_newtonianmechanics_3dynamics/ejss_model_SlidingDownInclinewee/SlidingDownInclinewee_Simulation.xhtml

Briefing Document: Block Sliding on an Incline Plane Simulation

1. Overview

This document reviews a JavaScript HTML5 applet simulation model titled "Block Sliding On An Incline Plane with Accelerometer," developed by Wolfgang Christian. The model is an interactive tool designed to illustrate the forces and dynamics of a block sliding on an inclined plane. It leverages the accelerometer in mobile devices (or a simulated tilt on computers) to demonstrate the effect of gravity on the block. This simulation is intended as an educational resource, providing a visual and interactive way for users to understand the principles of inclined plane physics. The tool is part of the Open Educational Resources / Open Source Physics @ Singapore initiative, highlighting its accessibility and open-source nature.

2. Key Themes & Concepts

Forces on an Inclined Plane: The primary focus is on the forces acting on a block resting or sliding on an inclined plane. This includes:
Gravitational Force (Weight): Represented in the simulation by a black arrow, this force is always directed downwards.
Normal Force: Represented in the simulation by a red arrow, this force acts perpendicular to the surface of the incline.
Frictional Force: Represented in the simulation by a green arrow, this force opposes the motion or the tendency of motion of the block.
Dynamics of Motion: The simulation showcases how the interplay of these forces leads to different dynamic behaviors of the block:
Static Friction: The force that prevents the block from moving when at rest on the incline.
Kinetic Friction: The force that opposes the motion when the block is sliding.
Acceleration: How the net force on the block determines its acceleration down or up the incline.
Use of Accelerometer: The simulation leverages the accelerometer of mobile devices to make the simulation's tilt align with the user's device, enabling an intuitive and interactive learning experience. A "No sensor" mode is available for computers, which simulates tilting.
Interactive Parameter Control: Users can manipulate parameters such as:
Initial position and velocity of the block.
Static and kinetic coefficients of friction.
Angle of the incline (via physical device tilting or "no sensor" mode).
Inquiry-Based Learning: The simulation is designed to promote inquiry-based learning through a series of physics exercises, where students can verify their understanding through simulation results.

3. Important Ideas & Facts

Accelerometer Integration: The simulation uses "the accelerometer on your mobile device to read the direction of the gravitation field g." This integrates real-world interaction with the simulated physics. However, note that "continuously reading the accelerometer may drain the battery on a mobile device" and the simulation automatically pauses after 4 minutes to conserve battery power.
Force Diagram: A key feature is the interactive display of a "force body (free body) diagram showing the normal force (red), the gravitational force (black), and the force of friction (green)." This visual aid helps users understand the vector nature of these forces.
Coefficient of Friction: The simulation allows users to adjust both static (μs) and kinetic (μk) coefficients of friction which directly affects the friction force. The simulation shows that friction is not constant, explaining how it changes as the surface tilts which contrasts with the commonly used formula " f = μs N."
Simulation Controls:The "Play" button starts the simulation after setting parameters.
"Initial values, such as x0 and v0, can be set when the simulation is paused but not when the simulation is running."
The block can be "dragged when the simulation is paused."
The "reset button returns the system to its default state while the reset time button returns the system to the previous values of x0 and v0."
Range of Block Motion: The block is "constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers," allowing analysis of the block's motion within a defined distance.
Limitations: There's a maximum allowed value of μs which is five.
Development Tool: The model was created using the Easy Java Simulations (EJS 5) tool, which creates standalone JavaScript programs.
Open Source Nature: The simulation is part of an open educational resource, emphasizing its purpose for learning and adaptation. The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License.

4. Key Quotes

"This simulation uses the accelerometer on your mobile device to read the direction of the gravitation field g."
"A force body (free body) diagram showing the normal force (red), the gravitational force (black), and the force of friction (green) is shown."
"The formula for the force of friction f when the block is not slipping is often given in textbooks as f = μs N where N is the magnitude of the normal force. But the simulation shows that the force of friction changes as the surface tilts. Explain why the force of friction is not constant."
"Initial values, such as x0 and v0, can be set when the simulation is paused but not when the simulation is running."
"The block is constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers."
"Because continuously reading the accelerometer may drain the battery on a mobile device, you must run the simulation to read the device tilt. The simulation will automatically pause after 4 minutes to conserve battery power."

5. Physics Exercises and Applications

The "Physics Exercises" section includes nine questions designed to guide user exploration and understanding: * Drawing force diagrams for blocks on horizontal and inclined surfaces. * Explaining why friction changes with tilt. * Investigating effects of varying static and kinetic friction coefficients (including negative coefficients). * Deriving expressions for maximum tilt angles and block movement, and verifying these expressions through the simulation. * Analyzing a number of scenarios with various starting conditions, inclines and speeds, to predict the block's motion and verifying via the simulation.

6. Intended Audience & Use

The model is intended for learners of physics at various levels, especially those learning about Newtonian mechanics and forces. It can be used in:

Classroom settings with or without mobile devices.
Individual learning for practice and exploration of physics concepts.
As a tool for teachers to demonstrate and illustrate physical principles.

7. Conclusion

The "Block Sliding On An Incline Plane with Accelerometer" simulation is a powerful and user-friendly educational tool. By combining interactive simulation with real-world sensor input, it enhances the learning experience for students and instructors studying mechanics. The open-source nature encourages the use and adaptation of this tool for educational purposes. The detailed exercises and user adjustable parameters promote an inquiry based learning model.

Inclined Plane Simulation Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

How does the inclined plane simulation use the accelerometer on a mobile device?
What are the three forces displayed in the free-body diagram in the simulation?
Why can initial values like position and velocity only be adjusted when the simulation is paused?
Explain why the force of friction changes as the angle of the incline changes, even though the formula for friction is f = μsN
In the simulation, what happens if you set the static coefficient of friction (μs) to a value less than the kinetic coefficient of friction (μk)?
What does the reset button do in the simulation, and how is it different from the reset time button?
In the context of the simulation, what is the maximum allowed value for the static coefficient of friction (μs), and what does that suggest?
If the inclined plane is horizontal, and the block is given an initial velocity to the right, what force will slow it down?
If the block is moving down an incline, what must the relationship between the force of gravity along the incline and the force of friction be for the block to move at a constant speed?
Why is the simulation designed to automatically pause after 4 minutes?

Quiz Answer Key

The simulation uses the accelerometer on a mobile device to detect the direction of the gravitational field, g. It uses this data to determine the orientation of the device and thus the angle of the simulated incline.
The free-body diagram shows the normal force, the gravitational force, and the force of friction acting on the block, each color-coded for easy identification.
The simulation requires a pause to prevent conflicts between user input and the ongoing calculations as the simulation is running, and allows you to drag the block.
The force of friction is dependent on the normal force (N) which changes as the angle of the incline changes. While f = μs N is the formula, N changes as the tilt of the inclined plane changes so friction is also not constant.
When μs is less than μk, the simulation shows the block immediately sliding, which is physically consistent since static friction must always be equal or greater than kinetic friction.
The reset button restores all parameters to their default states, while the reset time button only resets the initial position and initial velocity of the block.
The maximum allowed value for μs is 5, which is a high value and represents a surface with a large static friction.
In a horizontal setup, the block will slow down due to kinetic friction, which is a force acting opposite the block's motion.
For the block to move at constant speed down the incline, the component of gravitational force acting down the incline must be equal in magnitude to the kinetic friction force acting up the incline, so that the net force is zero.
The simulation automatically pauses after 4 minutes to conserve battery power, as constantly reading the accelerometer can be a significant drain.

Essay Questions

Instructions: Answer the following essay questions using information from the provided source material. Each response should demonstrate a thorough understanding of the concepts presented.

Analyze the relationship between the static coefficient of friction, the angle of the incline, and the point at which a block begins to slide. How can the simulation be used to empirically determine the relationship between these variables?
Discuss the significance of the free-body diagram in analyzing the motion of the block. How does the simulation's visualization of these forces improve the understanding of inclined plane dynamics?
Explain how to use the simulation to verify analytical derivations of motion. Provide an example for each of the three scenarios given in exercises 6, 7, and 8 in the provided source material.
Compare and contrast the behavior of the block under different values of static and kinetic friction coefficients. Use data from the simulations to predict what will happen to the block’s movement.
Considering the limitations of the simulation, how accurately does it represent real-world scenarios of blocks sliding on an inclined plane? What simplifications are made, and how could the model be extended for future versions?

Glossary of Key Terms

Accelerometer: A device that measures proper acceleration, often used to detect the orientation and tilt of a device relative to the earth's gravity.
Free-body Diagram: A visual representation of all forces acting on an object.
Normal Force (N): The force exerted by a surface to support the weight of an object on it; it acts perpendicular to the surface.
Gravitational Force: The force of attraction between objects with mass, typically denoted by the symbol ‘g’ in the context of the acceleration of gravity near the earth’s surface.
Static Coefficient of Friction (μs): A dimensionless value representing the ratio of the maximum static frictional force to the normal force, which determines how difficult it is to start an object moving.
Kinetic Coefficient of Friction (μk): A dimensionless value representing the ratio of the kinetic frictional force to the normal force, which determines how much a surface resists the movement of an object.
Friction Force (f): A force that opposes motion between two surfaces in contact.
Incline Plane: A plane surface angled relative to the horizontal or the vertical.
Initial Position (x0): The starting location of an object when the simulation begins.
Initial Velocity (v0): The starting speed and direction of an object when the simulation begins.
Simulation: A digital model created to approximate the behavior of a real-world system, like the block on the incline plane.

Block On An Incline

Physics Exercises:

Draw a force body diagram for a block on a horizontal surface (θ = 0°), labeling all forces.
Draw a force body diagram for a block on a surface inclined at an arbitrary nonzero angle of θ, labeling all forces.
The formula for the force of friction f when the block is not slipping is often given in textbooks as f = μ_sN where N is the magnitude of the normal force. But the simulation shows that the force of friction changes as the surface tilts. Explain why the force of friction is not constant.
What happens in the simulation if you set μ_s less than μ_k? Give a physical reason why the response is reasonable. What happens in the simulation if you set μ_s or μ_k less than zero? Give a physical reason why the response is reasonable.
Derive an expression for the maximum tilt angle without the block slipping (v_x= 0) when μ_s= {0.5, 0.6, 0.8, 1.0, 5.0}. Verify with the simulation. Note that the maximum allowed value of μ_s is five in this simulation.
The block is constrained to move from x = 1 (m) to x = 9 (m) by the end bumpers. Suppose ϴ = 0°, and the block is given an initial speed, v = 3 m/s to the right. Derive an expression for how far the block will move. Verify with the simulation if the static coefficient of friction is μ_s= 0.5 and the kinetic coefficient of friction is μ_k= 0.4.
Suppose θ = -30°, and the block starts from rest at x = 1 (m) with a speed of 3 (m/s) up the incline. Derive an expression for how far the block moves up the incline. Verify with the simulation if μ_s= 0.6 and the kinetic coefficient of friction is μ_k= 0.4.
Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Will the block stop before it reaches the end bumper if μ_s= 0.6 and the kinetic coefficient of friction is μ_k= 0.4? If not, what is the speed when the block reaches the bumper. Derive an expression for the block to move at constant speed down the incline and verify with the simulation.
Suppose θ = +30°, and the block starts from rest at x = 1 (m) with a speed of 1 (m/s) down the incline. Derive a value for μ_k for the block to stop sliding just before it reaches the end bumper. Verify with the simulation.

Credits:

Version:

http://www.opensourcephysics.org/items/detail.cfm?ID=14054 Wolfgang Christian, Colleen L. Countryman, and Francisco Esquembre

Other Resources:

https://www.geogebra.org/m/Stu7gKyg Rotation: Rolling Motion by ukukuku

FAQ

1. What is the purpose of the "Block Sliding On An Incline Plane" simulation?

This simulation is designed to illustrate the forces and dynamics involved when a block slides on an inclined surface. It allows users to visualize concepts such as gravitational force, normal force, and friction. By manipulating parameters like initial position, initial velocity, and friction coefficients, users can test their understanding of inclined plane dynamics and compare their predictions with the simulation results. The simulation uses an accelerometer on mobile devices to read the direction of gravity.

2. How does the simulation work on different devices?

On mobile devices (tablets or smartphones) the simulation leverages the device's accelerometer to detect the tilt angle. Users might need to lock the screen orientation to maintain a consistent view as they tilt. On computers without an accelerometer, a "No sensor" mode is available. This mode simulates a tilted device in the view, allowing the same experiments and data to be obtained.

3. What are the key forces visualized in the simulation?

The simulation includes a force body (free body) diagram that visually represents three key forces acting on the block:

Normal Force (Red): The force exerted by the surface on the block, perpendicular to the surface.
Gravitational Force (Black): The force of gravity pulling the block downwards towards the center of the Earth.
Friction Force (Green): The force that opposes the motion of the block, either static or kinetic.

4. How can users interact with the simulation?

Users can interact with the simulation in several ways:

Setting Initial Conditions: When the simulation is paused, users can set the block's initial position (x0) and initial velocity (v0). These settings are non-editable while the simulation is running.
Adjusting Friction: Users can modify both the static (μs) and kinetic (μk) coefficients of friction when the simulation is paused.
Dragging the Block: The block can be dragged to different positions while the simulation is paused.
Resetting: A reset button returns the system to its default state while a reset time button returns the system to the previous values of x0 and v0.
Play and Pause: The user has full control over playing and pausing the simulation, which is necessary to view the results.

5. Why is the friction force not constant as the incline angle changes?

The simulation demonstrates that the force of friction is not constant, even though textbooks often present the formula f = μs N. This is because the normal force (N) changes as the incline angle changes. On a horizontal surface, the normal force equals the weight of the block. As the surface tilts, the normal force decreases because a component of gravity now acts parallel to the inclined surface. Since friction depends on the normal force, it also changes as the angle of tilt is changed.

6. What happens if the static friction coefficient (μs) is less than the kinetic friction coefficient (μk), and why?

Setting μs less than μk in the simulation is not physically realistic. The static friction coefficient is always equal to or greater than the kinetic friction coefficient. If this were not the case, a block already moving would spontaneously require more force to keep it moving than it took to get it started. In reality, it is more difficult to initiate the movement of an object on a surface than to maintain it once it is moving. This can be seen in the simulation that does not provide this type of behavior.

7. What are some specific physics exercises that can be explored with the simulation?

The simulation provides several exercise examples that users can explore:

Deriving expressions for maximum tilt angles before slipping for varying static friction coefficients.
Calculating how far a block will move on a horizontal surface, given an initial velocity and friction coefficients.
Calculating how far up an incline a block will move given initial velocity and friction coefficients.
Predicting whether a block will stop before reaching the end bumper on an incline, given initial velocity, friction coefficients, and incline angles.
Calculating the kinetic friction coefficient needed to bring a moving block to a stop at a specific distance from a set starting point on an incline.

These exercises promote an understanding of the relationship between incline angles, coefficients of friction, forces and displacement.

8. What is the purpose of the simulation pausing automatically after 4 minutes?

The simulation pauses automatically after 4 minutes to conserve battery power on mobile devices. This is because continuously reading data from the device's accelerometer can drain battery quickly. Users must run the simulation to capture the device's tilt information and continue experimentation.

Breadcrumbs

📐Block Sliding On An Incline Plane with Accelerometer JavaScript HTML5 Applet Simulation Model

About

Block On An Incline

Physics Exercises:

Credits:

Translations

Credits

Inclined Plane Simulation Study Guide

Quiz

Quiz Answer Key

Essay Questions

Glossary of Key Terms

Block On An Incline

Physics Exercises:

Credits:

Version:

Other Resources:

FAQ

1. What is the purpose of the "Block Sliding On An Incline Plane" simulation?

2. How does the simulation work on different devices?

3. What are the key forces visualized in the simulation?

4. How can users interact with the simulation?

5. Why is the friction force not constant as the incline angle changes?

6. What happens if the static friction coefficient (μs) is less than the kinetic friction coefficient (μk), and why?

7. What are some specific physics exercises that can be explored with the simulation?

8. What is the purpose of the simulation pausing automatically after 4 minutes?