
About
For Teachers
- Ripple tank with sources in phase.mp4
Credits
Author: video: lookang, model: lookang, using YJC's ripple tank setup thank to jimmy goh
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.
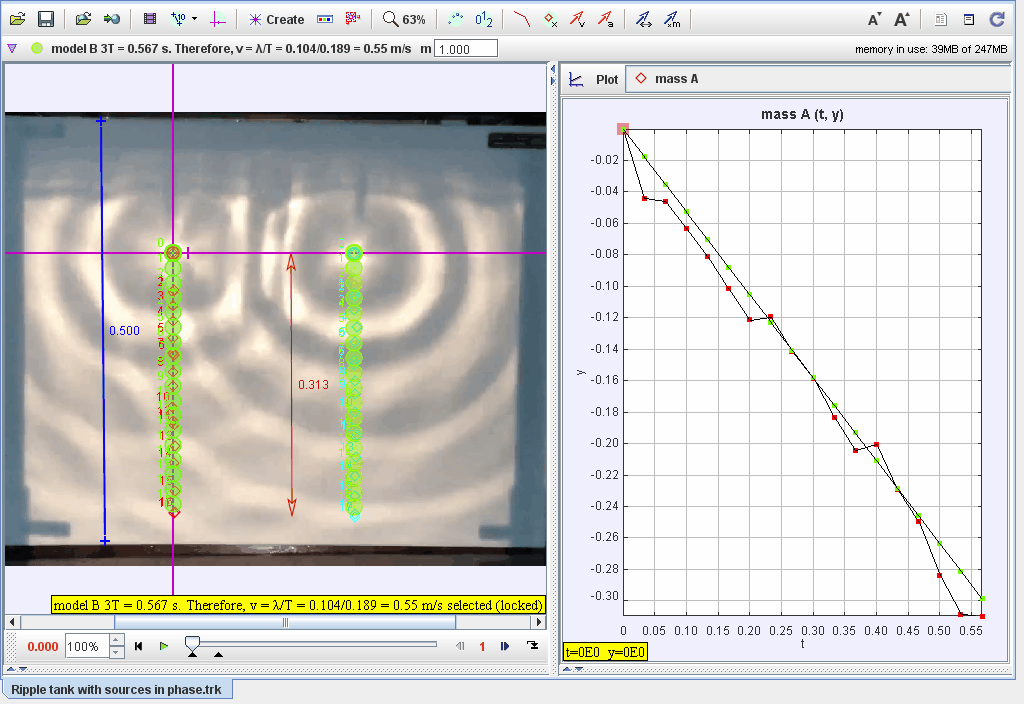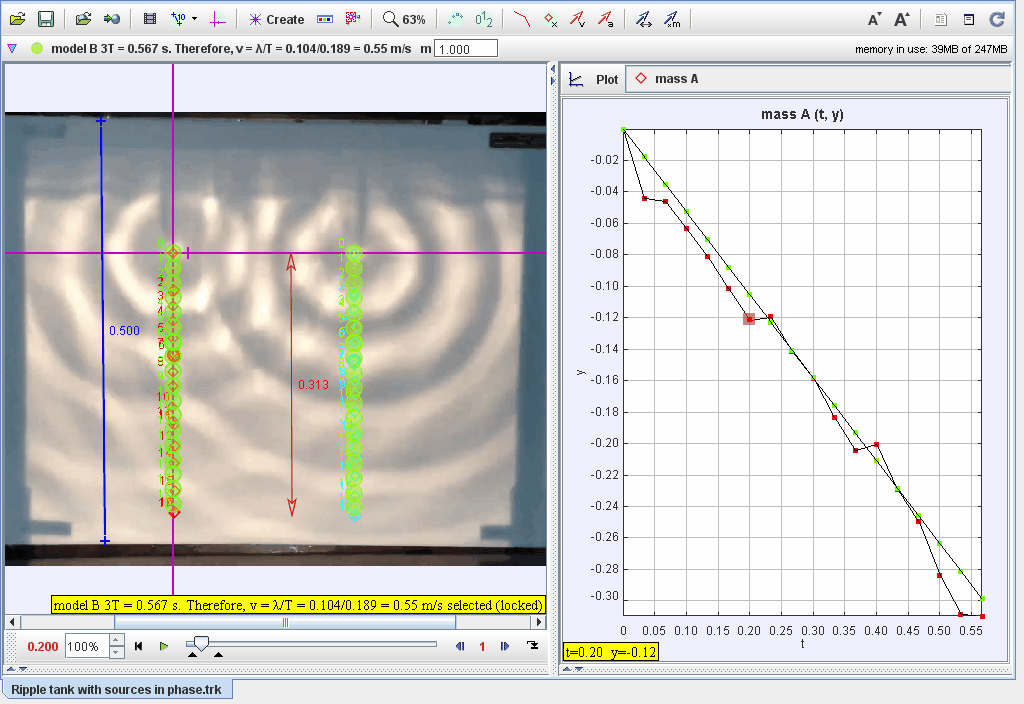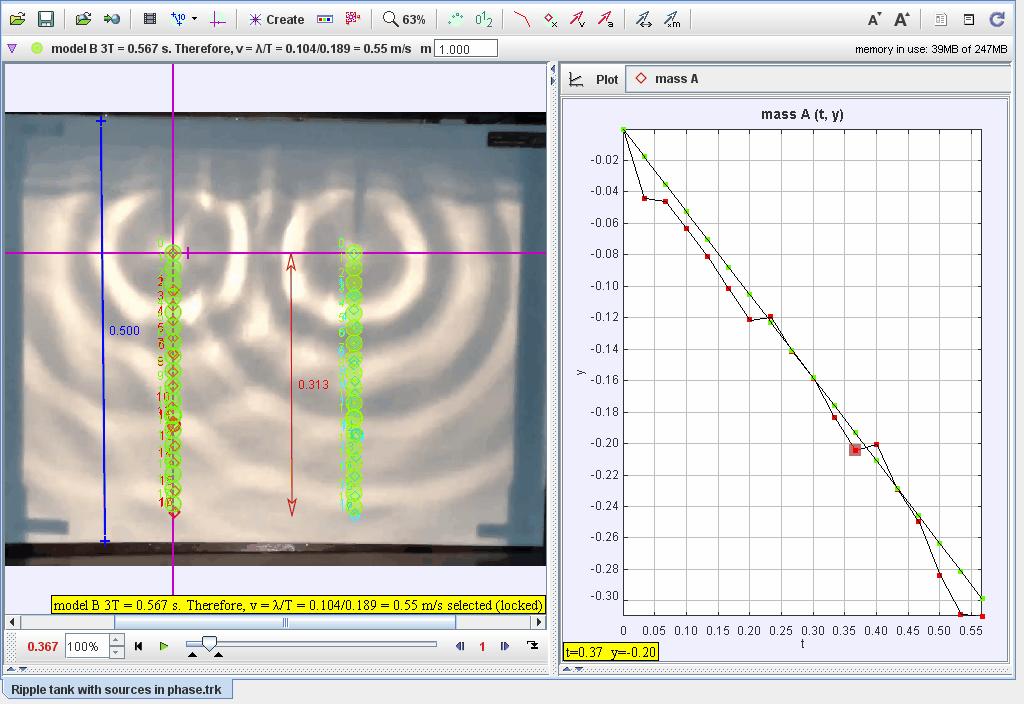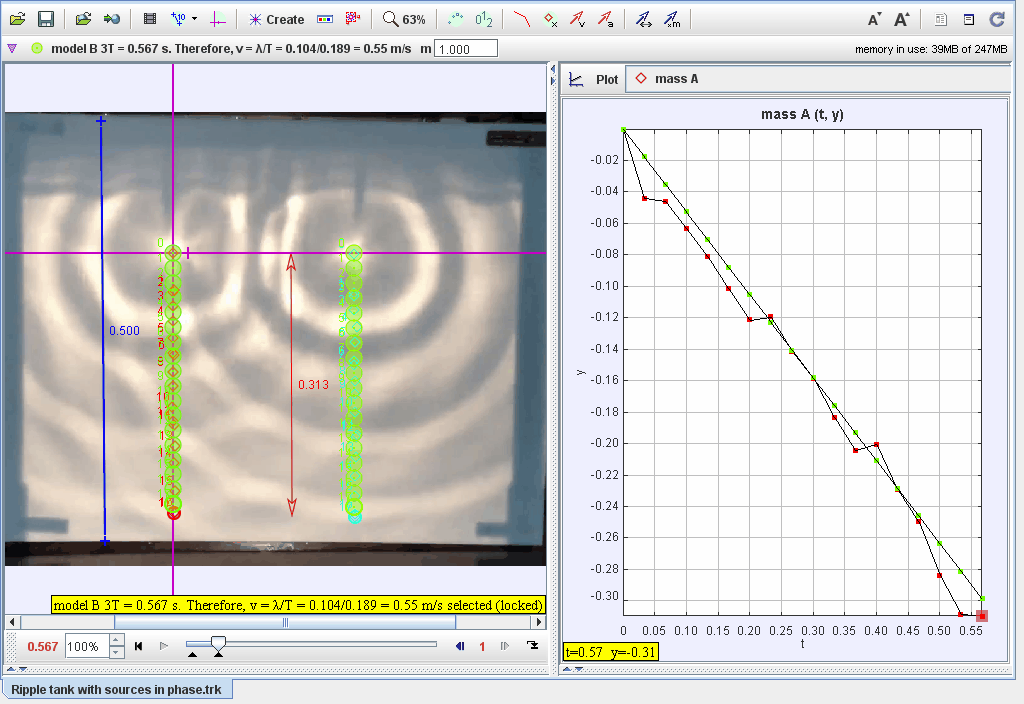
Document Brief: Modeling Two In-Phase Water Wave Sources Using Tracker
This document focuses on the analysis of two water wave sources oscillating in phase and traveling at constant velocities. The system demonstrates constructive and destructive interference patterns resulting from in-phase wave propagation, visualized through ripple patterns in a ripple tank.
Purpose:
To investigate the behavior of water waves generated by two in-phase sources, study the interference patterns formed, and validate the theoretical wave properties using experimental data.
Key Features:
- Visualization of interference patterns formed by in-phase wave sources.
- Analysis of wave properties such as amplitude, wavelength, and phase.
- Validation of constructive and destructive interference in a ripple tank.
Study Guide: Modeling In-Phase Water Waves
Learning Objectives:
- Understand the concept of wave interference from in-phase sources.
- Analyze interference patterns to identify regions of constructive and destructive interference.
- Validate theoretical predictions of wave behavior with experimental observations.
Step-by-Step Guide:
-
Setup and Calibration:
- Import the ripple tank video with two in-phase water wave sources into Tracker.
- Calibrate the scale using visible markers or references within the tank.
-
Tracking Wave Motion:
- Track the positions of the wavefronts generated by both sources.
- Measure the displacement (yy) of the water surface at different points over time.
-
Wave Equation and Interference:
- Define the wave functions for the two sources:
- Source 1: y1(x,t)=Asin(kx−ωt+ϕ1)
- Source 2: y2(x,t)=Asin(kx−ωt+ϕ2)
- where ϕ1=ϕ2=0 for in-phase sources.
- Resultant wave: y(x,t)=y1+y2=2Acos(Δx2)sin(kx−ωt)
- Analyze constructive interference (Δx=nλ) and destructive interference (Δx=(n+1/2)λ).
- Define the wave functions for the two sources:
-
Graphical Analysis:
- Plot displacement vs. time for points along the wavefront.
- Identify nodes (destructive interference) and antinodes (constructive interference) in the ripple pattern.
-
Applications:
- Study interference in water waves and sound waves.
- Explore principles of wave superposition in physical systems.
Tips for Success:
- Ensure precise tracking of the wavefronts for accurate analysis.
- Compare experimental interference patterns with theoretical predictions for validation.
FAQ: Constant Velocity Water Wave 2 Source In-Phase Model
1. What does in-phase mean for wave sources?
In-phase wave sources oscillate with the same frequency and phase (ϕ1=ϕ2), resulting in synchronized wavefronts.
2. What causes interference patterns?
Interference patterns are formed when waves overlap. Constructive interference occurs at points where wave crests meet, and destructive interference occurs where crests meet troughs.
3. How are nodes and antinodes formed?
- Nodes: Points of destructive interference where waves cancel (y=0).
- Antinodes: Points of constructive interference where waves reinforce (y=±2A)
4. What do the graphs of displacement vs. time show?
The graphs show periodic oscillations, with points of maximum amplitude corresponding to antinodes and zero amplitude corresponding to nodes.
5. How is the resultant wave equation derived?
The resultant wave is the sum of the individual wave equations:
y(x,t)=y1(x,t)+y2(x,t)
This results in an interference pattern dependent on the phase difference and path difference between the waves.
6. What are practical applications of this model?
- Understanding wave interference in acoustics, optics, and water systems.
- Designing systems that exploit constructive or destructive interference (e.g., noise-canceling headphones).
- Demonstrating superposition principles in physics education.
7. Can this model analyze out-of-phase sources?
Yes, by setting a phase difference (ϕ1−ϕ2=Δϕ), the model can analyze out-of-phase wave interference.
- Details
- Parent Category: 03 Waves
- Category: 02 Superposition
- Hits: 8923
