
About
For Teachers
Credits
Author: video: kim kia, model: lookang
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.
Document Brief: Bungee Jump Energy Analysis Using Tracker Software
This document details the use of Tracker software to study the motion of a bungee jumper, focusing on the energy transformations during free fall and elastic extension. The experiment highlights concepts like gravitational potential energy, kinetic energy, and elastic potential energy, using graphical tools to correlate them with the motion of the object.
Purpose:
To analyze energy transformations and motion in a bungee system, facilitating a deeper understanding of conservation of energy and elastic dynamics.
Key Features:
- Visualization of free-fall motion and subsequent elastic extension.
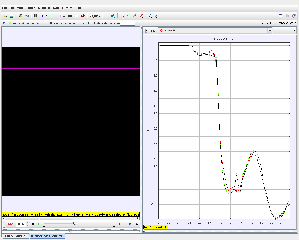
- Graphical representation of total energy (te) vs. time (t).
- Real-time tracking of displacement and energy states.
- Identification of key moments: free fall, maximum extension, and rebound.
Study Guide: Understanding Energy in Bungee Jump Systems
Learning Objectives:
- Comprehend the principles of energy conservation in dynamic systems.
- Analyze the transformation of gravitational potential energy into kinetic and elastic potential energy.
- Understand energy losses (if any) during the motion due to factors like air resistance.
Step-by-Step Guide:
-
Setup and Calibration:
- Import the video of the bungee jump into Tracker.
- Define the coordinate system and scale for accurate measurements (e.g., setting the vertical axis for motion tracking).
-
Tracking Motion:
- Mark the mass (bungee object) frame by frame to record its motion path.
- Observe the plotted green and red points representing tracked positions and energy data.
-
Energy Graph Analysis:
- Examine the te (total energy) vs. time graph:
- During free fall, gravitational potential energy decreases while kinetic energy increases.
- At maximum extension, kinetic energy is minimal, and elastic potential energy is at its peak.
- Analyze the rebound phase for energy recovery and dissipation.
- Identify time intervals for free fall, elastic stretching, and oscillatory motion.
- Examine the te (total energy) vs. time graph:
-
Applications:
- Calculate the spring constant kk using Hooke’s law: F=kxF = kx, where xx is the extension.
- Discuss energy losses due to non-ideal factors like damping.
Tips for Success:
- Ensure precise scaling to avoid errors in energy calculations.
- Cross-reference theoretical energy values with measured data for validation.
FAQ: Bungee Jump Energy Tracker
1. What is the purpose of this experiment?
The purpose is to study energy conservation and transformation during a bungee jump, demonstrating real-life applications of gravitational and elastic potential energy.
2. Why does the total energy graph fluctuate?
Fluctuations may arise due to energy dissipation (e.g., air resistance) or measurement inaccuracies. In an ideal system, total energy remains constant.
3. How is elastic potential energy calculated?
Elastic potential energy (EeE_e) is calculated using 12kx2\frac{1}{2}kx^2, where kk is the spring constant and xx is the extension.
4. Can we determine the spring constant from this data?
Yes. Using the elastic extension data and Hooke’s law, you can derive the spring constant.
5. What are the assumptions made in this analysis?
- The spring follows Hooke’s law perfectly.
- Air resistance and other dissipative forces are negligible.
6. How does this relate to real-world bungee jumps?
This experiment mimics the physics of bungee jumping, helping engineers design safe systems by understanding energy transformations and limits of elasticity.
- Details
- Written by Kimkia
- Parent Category: 04 Energy & Fields
- Category: 07 Energy Work Power
- Hits: 6299
