Translations

Code	Language		Translator	Run
id	id	id

Credits

Fu-Kwun Hwang; Loo Kang Wee

http://iwant2study.org/lookangejss/02_newtonianmechanics_5turningeffectsofforces/ejss_model_blocktiltedwee/blocktiltedwee_Simulation.xhtml

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.blocktiltapp658507

Introduction

Property of a body for which a small angular displacement set up a restoring torque that tends to return the body to its original position. In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. An important property of systems at mechanical equilibrium is their stability.

Instruction

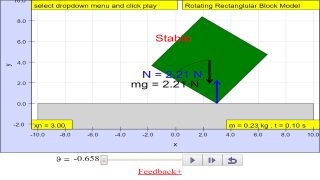
Drag the center of the block to make the block tilt with an angle. As long as the center of gravity stay inside the surface area of the object on the ground, the block will not fall out. Because the torque will always turn it back.
However, if the center of gravity was outside the surface area, the block will fall out.! You can also change width or height (resize) of the block within the simulation.

Key inquiry question: What are the characteristics and effects of forces in nature? 4. & 6. Turning effects of forces and Equilibrium of forces

• The moment of a force (or torque) = force x perpendicular distance from the pivot. The moment of a force is used in simple machines like the lever.

• Principle of moments states that for a body to be in rotational equilibrium, the sum of its clockwise moments about any point is equal to the sum of anticlockwise moments about the same point.

Key inquiry question: What are the characteristics and effects of forces in nature? 5 Centre of gravity and Stability

• The weight of a body may be taken as acting at a single point known as its centre of gravity; the position of which affects the stability of the body.

• Stability is a measure of a body’s ability to maintain its original position. Objects may be made more stable by lowering its centre of gravity or increasing its base area.

Sample Learning Goals

[text]

For Teachers

[text]

Research

[text]

Video

 How to Teach using Simulation Full HD video by Joseph Chua Pei Hwa Sec

 How to Teach using Simulation part 1/2 by Joseph Chua Pei Hwa Sec

 Video showing how to use effect of forces for mouse trap design

https://youtu.be/ABffYDM9EwU

 How to Teach using Simulation part 2/2 by Joseph Chua Pei Hwa Sec

 Version:

1. http://weelookang.blogspot.sg/2016/03/rotating-rectangular-block-model.html a remix by lookang
   
2. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=433.0 original Java simulation by Fu-Kwun Hwang

Other Resources

https://www.geogebra.org/m/xmx55cj5 by seng kwang

https://ggbm.at/qszfx35k by tan seng kwang

https://ggbm.at/sw3txavd by Vincent Lew and tan seng kwang

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}